سینماتیک

سینماتیک (از واژهٔ یونانی κινεῖν یا kinein به معنای حرکت‌کردن) گرفته شده ،سینماتیک شاخه‌ای از دانش مکانیک کلاسیک است که حرکت اجسام و سامانه‌ها (گروهی از اجسام)را بدون درنظرگرفتن نیروهای عامل حرکت بررسی می‌کند. در تهیه این مقاله تا جائی که امکان داشت توضیحات  و فرمول های ریاضی به صورت ساده ولی کامل تهیه شده است . مرجع اصلی این مقاله کتاب “فیزیک هالیدی جلد اول“می باشد و برای کسانی که مایلند دراین زمینه حرفه ای ترکار کنند توصیه می شود به اصل کتاب فیزیک هالیدی مراجعه وتمام تمرینات و مسائل  مربوطه را بدقت حل کنند.
نکته : قبل از مطالعه این مقاله بهتر است مقاله “ مکانیک “ را مطالعه کنید .

شکل شماره یک – فیزیک هالیدی

۱- واحدهای اندازه گیری

سنگ بنا و ستون علم فیزیک کمیت های فیزیکی می باشد درفیزیک هر چیزی که مقدار آن با یک عدد مشخص شده و قابل اندازه گیری باشدکمیت فیزیکی نامیده می شود در این بخش به صورت خیلی مختصر در مورد کمیت های اصلی فیزیکی توضیح داده می شود.

۱)اندازه شناسی و سیستم اندازه گیری

همچنان که توضیح داده شدقبل از کارکردن با فرمول های فیزیک ابتدا لازم است واحدهای اندازه گیری را که امروزه از آن استفاده می کنیم بشناسیم .در مورد واحدهای اندازه گیری که امروزه در همه کشورها و در همه علوم و فنون و تجارت و…به کار می رود (سیستم SI یا “دستگاه بین‌المللی یکاها “ ) می توانید به لینک هائی که در قسمت بعدی همین بخش گذاشته ایم مراجعه کنید .

۲)مقاله های در ارتباط با اندازه گیری و اندازه شناسی

در این سایت مقاله های مختلفی در این ارتباط منتشر شده است برای مطالعه  کامل تر می توانید به لینک هائی که در همین جا گذاشته ایم مراجعه کنید .
۱-۲) “ واحدهای غیر متریک “  : در مورد تاریخچه کلی اندازه گیری می باشد .
۲-۲) “سیستم متریک “  : در مورد تاریخچه سیستم متریک
۳-۲) “سیستم SI “  : در مورد تاریخچه سیستم SI به همراه جداول مربوطه
۳-۲) “اندازه گیری و اندازه شناسی “ : خلاصه سه مقاله قبلی به همراه تمامجدول ها و توضیحات مربوطه

۳)روش حل مسئله

نکته بسیار مهم درحل مسائل این است که برای جلوگیری از هرگونه اشتباه علاوه برفرمول های مربوطه باید به واحدهای آنها نیز توجه کرد . بهترین روش این است که واحد کمیت های اصلی و یا فرعی داده شده در مسائل را به واحد های اصلی همان کمیت ها تبدیل کرد (مثلا سانتیمتر را به متر و یا ساعت را به ثانیه و…)و بعد از حل مسئله جوابی که بدست می آید بر اساس واحدهای اصلی می باشد و بعد می توانیم به واحدهائی که مسئله خواسته برگردانیم . توضیحات بیشتر همراه با مثال در مقاله “اندازه گیری و اندازه شناسی “ بخش  پنجم “۵- دیمانسیون و حل مسئله “ می باشد که می توانید به آنجا مراجعه کنید .

۲–سینماتیک انتقالی(مفاهیم اولیه)

سینماتیک انتقالی از حرکت یک جسم به عنوان یک ذره شروع می کند و منظور از ذره جسمی است بدون بعد یعنی بدون طول و عرض و ارتفاع و بنابراین است مادراین نوع حرکت جسم را همچون نقطه ای درنظر می گیریم که جابجا می شودو کاری به حرکت تک تک نقاط جسم نداریم . 

۱)سرعت

 سرعت مسافت پیموده شده در واحد زمان می باشد . سرعت یک کمیت برداری می باشد یعنی علاوه بر مقدار جهت هم دارد. اگرحرکت مستقیم الخط یکنواخت باشدسرعت(ازنظر اندازه و جهت) مقدار ثابتی می باشد در غیراین صورت سرعت متغیر بوده و ماهر لحظه یک سرعت داریم که سرعت لحظه ای نامیده می شود و اگر کل مسافت را بر زمان پیموده شده تقسیم کنیم سرعت متوسط را داریم.
واحد اصلی سرعت درسیستم بین المللی یکاها (SI)m/s (متربرثانیه ) می باشد. ولی از واحدهای دیگری بخصوص کیلومتر درساعت (Km/h) هم استفاده می کنند .

 

۲)سرعت متوسط و سرعت لحظه ای

جسم متحرکی (مثلا اتوبوسی که فاصله دو شهر را می پیماید) در یک مسیر شروع به حرکت می کنددر جائی که جاده خلوت می باشد با حداکثر سرعت حرکت می کند بعضی اوقات بخاطر ترافیک سرعتش کم می شود و حتی مدتی هم توقف کامل می کند . بنابراین دو نوع تعریف سرعت داریم سرعت لحظه ای و سرعت متوسط
۱-۶)سرعت متوسط : طول کل مسافت پیموده شده تقسیم بر زمان پیمودن این مسافت است .
۲-۶) سرعت لحظه ای : سرعت لحظه ای سرعتی است که متحرک در هر لحظه دارد و یا به عبارتی سرعتی است که در هر لحظه عقربه سرعت سنج ماشین نشان می دهد .

۳)تفاوت تندی و سرعت

سرعت یک کمیت برداری می باشدبنابراین هم جهت و هم اندازه دارد با این حساب اگر متحرکی مسیری را با سرعت های مختلف طی کند برای محاسبه سرعت متوسط یک راهش این است که مسیر اصلی را به قسمت های مختلف(که درهر قسمت سرعت ازنظر اندازه و جهت ثابت باشد)تقسیم کرده وسرعت رادر این مسیرهای فرعی با هم جمع کرد و بر تعداد مسیرها تقسیم کرد این جمع کردن سرعت ها باید به طریق برداری انجام شود یعنی در هرقسمت بردار سرعت را بدست آورد و با بردار سرعت درقسمت دیگر مسیرجمع کرد.بنابراین اگر متحرک در یک مسیر بسته از نقطه ای حرکت کرده و به نقطه اول برگردد سرعت متوسط درنهایت صفر می شود (شکل شماره ۲(درحالی که مسافت زیادی را ممکن است طی کرده باشد . و اگر در مسیر مارپیچی حرکت کرده باشد برای بدست آوردن سرعت آن پاره خط جهت داری را از نقطه شروع به نقطه جابجائی وصل می کرده که این جهت جابجائی را نشان می دهد و فاصله بین دو نقطه مبدا و مقصد را بر زمان کل جابجائی تقسیم می کنیم (شکل شماره ۳)
در حالی که تندی کمیتی اسکالر است و جهت ندارد برای بدست آوردن تندی کل مسیر جابجاشده (فلش های زرد درشکل۳ ) را بر زمان جابجائی تقسیم می کنیم دراین صورت هیچ اطلاعاتی در مورد مسیر نمی توانیم کسب کنیم .

  

شکل شماره ۲-متحرک مسیر بسته ای را طی کرده بنابراین سرعت متوسط او صفر می شود .

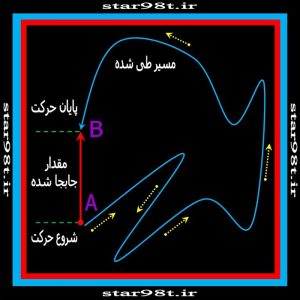
 شکل شماره ۳ – برای بدست آوردن سرعت متوسط ابتدا و انتهای مسیر را بهم وصل کرده بردار حاصل را بر زمان تقسیم می کنیم ولی برای محاسبه تندی کل مسیر را بر زمان تقسیم می کنیم 

 ۴)شتاب

در فیزیک شتاب را مقدار تغییر سرعت در واحد زمان تعریف می کنند . از آنجائی که سرعت کمیت برداری می باشد شتاب هم کمیت برداری می شود . اگر سرعت از نظر اندازه تعغیری نکند ولی از نظر جهت تعغیر کند باز هم حرکت شتابدار خواهیم داشت . 

واحد اصلی شتاب در سیستم متریک m/S₂(متربر مجذورثانیه ) می باشد .

۵)انواع شتاب

در تعریف شتاب مقدار تغییر سرعت در واحد زمان را ذکر کردیم حال این تعغیر سرعت می تواند نرخ ثابتی داشته باشد (شتاب ثابت) یا تعغیر کند (شتاب متغیر) همچنین شتاب می تواند افزاینده باشد یا کاهنده که در اینجا شتاب افزاینده و کاهنده را توضیح می دهیم .
دقت کنید وقتی از شتاب افزاینده و کاهنده صحبت می کنیم حرکت باید مستقیم الخط باشد در این صورت سرعت و شتاب تنها دو جهت(رو به جلو و عقب)دارند و بنابراین اندازه بردار سرعت با تندی برابر می شود .
۱-۴) شتاب افزاینده : اگر در زمان مورد نظرسرعت زیاد شود( از نظر اندازه یعنی تندی زیاد شود) سرعت ثانویه “ V ” بیشتر از سرعت اولیه “V₀” می شود بنابراین  شتاب افزاینده می باشد V>V₀ و بنابراین a>0
در این نوع شتاب راستای شتاب در جهت راستای سرعت می باشد . یعنی مقدار شتاب مثبت می باشد.
۲-۴) شتاب کاهنده:اگر در زمان مورد نظر سرعت کم شود یعنی سرعت ثانویه “ V ” کمتر از سرعت اولیه “ V0 ” باشد شتاب کاهنده می باشد V<V₀ و بنابراین a<0 از نمونه های این نوع حرکت شتابدار اتومبیلی است که قصد توقف داشته و ترمز می کند . در این نوع شتاب منفی و جهت آن مخالف جهت سرعت می باشد .

۶)سقوط آزاد

سقوط آزاد نوعی حرکت شتابدار است که با شتاب ثابت در مجاورت زمین رخ می دهد .در صورتی که یک جسم را در ارتفاع معینی (ارتفاع h)در اطراف زمین رها کنیم . و از مقاومت هوا و نیروهای دیگر (وزش باددر راستای افقی و…) صرف نظر کنیم .جسم در راستای عمودی و تنها تحت تاثیر وزن خود با شتاب ثابت “g” (که مقدار آن حدود ۸/۹ می باشد) به سمت زمین سقوط می کند بنابراین سقوط آزاد نوعی حرکت شتابدار (با شتاب ثابت g) می باشد که در راستای عمودی ( محورY) انجام می شود .
در حرکت سقوط آزاد مسیر شتاب همواره عمودی و به طرف مرکز زمین است(از بالا به پائین)بنابراین در صورتی که پرتابه ای از زمین به بالا رها شود شتاب کاهنده و مقدار آن منفی می شود. “a=-g=-9.8” و اگر پرتابه از ارتفاعی مشخص رها شود و یا با سرعت اولیه رو به پائین پرتاب شود شتاب مثبت می باشد .

۳- سینماتیک انتقالی(معادلات حرکت مستقیم الخط)

وقتی از حرکت صحبت می کنیم اولین مسئله جابجائی جسم می باشد ساده ترین حالت این است که این جابجائی با سرعت ثابت و در امتداد خط راست می باشد که به آن حرکت مستقیم الخط یکنواخت می گویند ولی حرکت حالت های پیچیده تری هم دارد می تواند این حرکت با شتاب ثابت ولی مستقیم الخط باشد و می تواند با شتاب متغیر باشد همچنین حرکت می تواند بجای مستقیم الخط بودن در دو بعد(درون صفحه)وحتی سه بعدی باشد . دراین بخش فقط حرکت مستقیم الخط را مورد بررسی قرار داده و در بخش های بعدحرکت در دو و یا سه بعد را هم مورد بررسی قرار می دهیم .

۱)پارامترهای مهم در حرکت شتابدار مستقیم الخط

در حرکت شتابدار چهار پارامتر را در نظر می گیریم (شتاب a،زمانt ،سرعتV ، مسافت x) که هر پارامتر یک مقدار اولیه یک مقدار ثانویه دارد . چون حرکت مستقیم الخط است می توانیم سرعت و شتاب و مسافت را اسکالر در نظر گرفته و فقط درجهت راست محور X را مثبت و در جهت چپ را منفی بگیریم

 

    

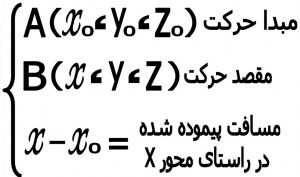
در صورتی که حرکت در راستای محورYیا Z باشد بجای اندیس X اندیس y و یا Z را قرار می دهیم.
از اینجا به بعد برای سادگی ابتدا حرکت را مستقیم الخط و در یک بعد (محور Xها) در نظر می گیریم .

۲)سرعت متوسط در حرکت شتاب دار مستقیم الخط

برای بدست آوردن سرعت متوسط در هرحرکتی ابتدا و انتهای بردار جابجائی را می توان مسافت پیموده شده در نظر گرفت بنابراین می توان نشان داد که در حرکت شتابدار مستقیم الخط با شتاب ثابت سرعت متوسط میانگین سرعت در ابتدا و انتهای مسیر می باشد یعنی :

۳)سرعت لحظه ای

سرعت لحظه ای که در هر لحظه عقربه سرعت سنج نشان می دهد عبارت است از مشتق مسافت نسبت به زمان یعنی ما معادله مسافت زمان را نوشته و نسبت به آن مشتق می گیریم معادله سرعت لحظه ای بدست می آید.حال حرکت یکنواخت و یا با شتاب ثابت و یا حتی شتاب متغیر باشد .

۴)رابطه بین سرعت و زمان و شتاب و مسافت (شرایط اولیه)

در این قسمت رابطه بین پارامترهای چهار گانه(شتاب a، زمانt ، سرعتV ، مسافت x)درحرکت شتابدار را بدست می آوریم .برای سادگی کار ابتدا حرکت در یک بعد را در نظر می گیریم (بنابراین نیازی به نوشتن معادلات به صورت برداری نداریم و به همان شکل ساده و اسکالر می نویسیم )مسافت پیموده شده را هم می توانیم با “d” نمایش بدهیم زمان را هم طول مدت زمانی که از مبدا حرکت کرده تا به مقصد برسیم در نظر گرفته و به طور مطلق با “t” نمایش می دهیم به همین ترتیب سرعت اولیه را با “V₀” و سرعت انتهای مسیر را هم با “V” و شتاب را هم با “a”نمایش می دهیم . بنابراین در مجموع چهار پارامتر داریم(V و V₀ یک پارامترحساب می شوند ) که چهار معادله (فرمول) را هم می توانیم بدست بیاوریم که در هر معادله یکی از پارامترها موجود نمی باشد به این ترتیب با داشتن دو پارامتر می توانیم دو پارامتر دیگر را هم بدست بیاوریم .
نکته : معمولا در بیشتر مسائل V₀ (سرعت اولیه )یا موجود است یا برابر صفر قرار داده شده است در صورتی که V₀ هم مجهول باشد به سه پارامتر از مجموع چهار پارامتر نیاز داریم .

۵)رابطه بین سرعت و زمان و شتاب و مسافت (محاسبه فرمول ها )

در این قسمت به ترتیب معادلات مربوط به حرکت شتابدار را بدست می آوریم .

۵-۱)معادله بدون مسافت : این معادله بر حسب پارامترهای زمان و مسافت و سرعت می باشد . برای نوشتن این معادله از تعریف شتاب استفاده می کنیم .

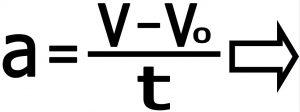
معادله شماره یک – رابطه بین سرعت و شتاب و زمان

۵-۲)معادله بدون شتاب : این معادله بر حسب پارامترهای سرعت و زمان و مسافت می باشد . برای نوشتن این معادله از تعریف سرعت متوسط استفاده می کنیم .

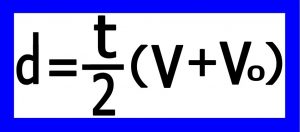
معادله شماره ۲ – رابطه بین : سرعت و مسافت و زمان

۵-۳)معادله بدون زمان : برای بدست آوردن این رابطه معادله شماره یک و دو را نوشته و دو طرف معادله را در هم ضرب می کنیم و با استفاده از اتحاد مزدوج می توانیم معادله شماره ۳ را نتیجه گیری کنیم .

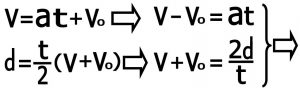
معادله شماره ۳ – رابطه بین سرعت و مسافت و شتاب

۵-۴)معادله بدون سرعت : این بار هم معادله ۱ و ۲ را نوشته ولی بحای این که در هم ضرب کنیم مقدار V را از معادله یک در آورده و در معادله ۲ جایگزین می کنیم و بعد از ساده کردن به معادله نهائی می رسیم .

 

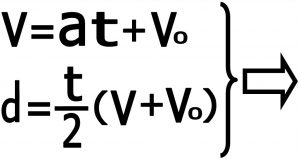
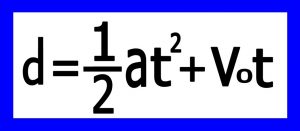
معادله شماره ۴ – رابطه بین مسافت و شتاب و زمان

۵)خلاصه معادلات

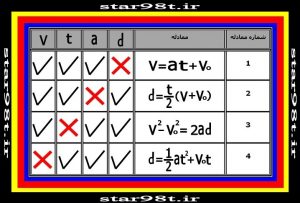
فرمول های یک تا چهار را می توان درجدولی به صورت زیر خلاصه کرد .

جدول شماره ۱ – فرمول های چهارگانه حرکت شتابدار

۴-حرکت چند بعدی

در بخش قبل برای نوشتن معادلات حرکت ابتدا فرض کردیم حرکت با شتاب ثابت و در امتداد خط مستقیم می باشددر اینجا این فرض را کنار گذاشته و حرکت را در دو بعد(حرکت در صفحه)درنظر گرفته و معادلات حرکت را می نویسیم همچنین می توانیم حرکت را سه بعدی کرده و در سه بعد بنویسیم (حرکت در فضا)در این بخش حرکت در دو یا سه بعد را درحالت کلی درنظر گرفته و بعد به انواع خاص حرکت در صفحه می پردازیم . 

۱)حرکت در دو یا سه بعد

برای نوشتن فرمول های زیر سه فرض را پیش کشیدیم . نخست آن که حرکت فقط در راستای خط راست( حرکت یک بعدی) را درنظر گرفتیم . دوم آن که مبدا حرکت را مبدا مختصات در نظرگرفیم و سوم اینکه مبدا زمان را هم لحظه شروع حرکت حساب کردیم . حال می توانیم همه این پیش فرض ها را کنار بگذاریم زیرا یک حرکت واقعی می تواند دردو یا سه بعد انجامشود.
در این صورت می توانیم بردار سرعت را به بردارهائی در راستای محورهای مختصات تجزیه کرده و معادله هر کدام را به صورت جداگانه بنویسیم در این صورت پارامترهای حرکت در راستای هر محور مستقل از دیگری می باشد و می توانیم بجای جدول شماره یک با اضافه کردن اندیس ها سه جدول مشابه برای معادلات حرکت بنویسیم . (جدول شماره ۲)این معادلات کاملا مستقل از هم می باشد و تنها وجه مشترک آنها زمان می باشد به عنوان مثال معادلات شماره یک تا چهارم در بخش قبل و با اضافه کردن اندیس ها به این صورت در می آید ( معادلات در راستای محورX)

حال اگر حرکت در راستای محور Y را بخواهیم بررسی کنیم بجای اندیس x می توانیم اندیس y را نوشته و برای حرکت در راستای محورZاندیس z را بنویسیم . پارامترهای حرکت پارامترهای چهارگانه (شتاب a، زمانt ، سرعتV ، مسافت x) در هر کدام مستقل از دیگری می باشد و تنها زمان بین آنها مشترک است .

۲)معادله حرکت چند بعدی

با داشتن مقادیر معلوم در امتداد هر محوری می توانیم معادله حرکت را در امتداد هر محور به صورت جداگانه بنویسیم برای مربوط کردن آنها به همدیگر و بدست آوردن یک معادله واحد(همچنان که در بخش حرکات پرتابی توضیح می دهیم) می توانیم زمان (t) را بین آنها حذف کرده و معادله واحدی بر حسب xوyوz بدست بیاوریم .    

۳)جدول حرکت چند بعدی

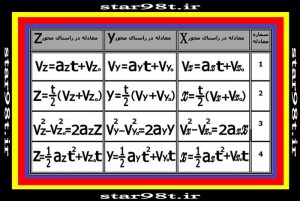
برای نوشتن جدول معادلات حرکت چند بعدی می توانیم معادلات را ساده تر کرده و مقدار t-t₀=t قرار داده و    x-x₀=x و همچنین y-y₀=y و z-z₀=z قرار بدهیم بنابراین داریم .

جدول شماره ۲ – معادلات حرکت در دو و سه بعد

۴)حرکات پرتابی

حرکات پرتابی نمونه ای ازحرکت در صفحه است که در روی زمین بسیار با آن سرو کار داریم در این حرکت جسم با یک زاویه نسبت به افق پرتاب می شود. (نمونه ملموس آن گلوله توپی که تحت زاویه ” θ” نسبت به افق شلیک می شود).با تجزیه سرعت اولیه در دو راستای عمود بر هم(راستای افقی موازی افق و راستای عمودی در جهت عمود بر افق) می توانیم معادلات هر کدام را جداگانه نوشته و بررسی کنیم .
نظر به اهمیت آن حرکات پرتابی را در یک بخش جداگانه مورد بررسی قرار می دهیم .

۵) حرکت دایره ای یکنواخت

حرکت دایره ای یکنواخت نمونه ای از حرکت در صفحه می باشد که در آن جسمی که تحت تاثیر نیروئی (مثلا نیروی جاذبه ) قرار دارد در یک مسیر دایره ای حرکت می کند بنابراین حرکت در امتداد یک خط راست قرار نداشته پس حرکت مستقیم الخط حساب نمی شوداگر مسیرحرکت را دایره کامل بگیریم اندازه سرعت(تندی) را می توانیم ثابت در نظربگیریم و چون سرعت کمیتی برداری است بخاطر جابجا شدن مسیر بردار سرعت (با وجودی که مقدار آن ثابت است ) حرکتی یکنواخت نیز نبوده و حرکت شتابدار حساب  می شود که بردار شتاب همیشه بر بردار سرعت عمود بوده و در جهت مرکز دایره می باشد . و از این رو اندازه بردار سرعت تعغیری نمی کند . در شکل شماره ۵ نشان می دهیم که این شتاب ازکجا و چگونه بوجود می آید . و مقدار آن چقدر است .

 

شکل شماره ۴ – شتاب جانب مرکز سیاره ها را در مدار نگه می دارد .

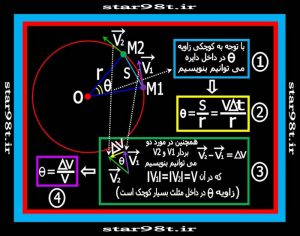
شکل شماره ۵ – محاسبه شتاب زاویه ای شتاب جانب مرکز

قبل از مطالعه بقیه مطالب به شکل و فرمول های آن دقت کنید .

همانطور که در شکل شماره ۵ می بینید جسمی که روی مسیر دایره ای حرکت می کند از نقطه M1 به نقطه M2 رسیده است. بردارحرکت در نقطهM1 را با V1 و بردار حرکت در نقطهM2 را با V2 نشان می دهیم اگر فاصله M2 و M1 به اندازه کافی کوچک باشد رابطه شماره ۲و ۴را مستقلا می توانیم نتیجه بگیریم (چرا ؟) و بنابراین از رابطه ۲ و ۴ با توجه به تعریف شتاب می توانیم بنویسیم .

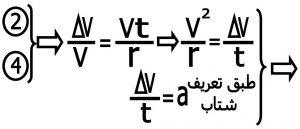
حرکت دایره ای یکنواخت در طبیعت از حرکت سیاره ها در مدار ستاره ها تا قمرها و ماهواره ها در مدار سیارات و… بسیار دیده شده از این رو مطالعه آن بسیار مهم می باشد.
نکته۱ : در “شکل شماره ۵ “مثلث های همچنین  OM1M2و همچنینΔVV1V2  متساوی الساقین هستند می توان ثابت کرد که درحالت حدی که زاویه راس مثلث به سمت صفر میل می کند اندازه زاویه برحسب رادیان برابر است با قاعده مثلث تقسیم بر ساق یعنی درمثلث ΔVV1V2 داریم : V/ΔV = θ
همچنین در مثلثOM1M2 داریم S/r = VΔt/r = θ (S مسافت پیموده شده می باشد که برابر سرعت ضرب در زمان می باشد یعنی S = VΔt )
نکته ۲: در فرمول زمان طی شده یعنی Δt را به اختصار t گرفتیم .
نکته۳ : درحالت حدی که زاویه کوچک باشد اندازه کمان (S) برابر با اندازه وتر (S)می شود .

۵-حرکت پرتابی

حرکات پرتابی نمونه ای ازحرکت در دو بعد(محور عمودی Y و محور افقی X) می باشد .(درحالت خاص می توان در سه بعد هم تعمیم داد)درصورتی که یک جسم تنها تحت تاثیر نیروی جاذبه بوده (ازمقاومت هوا صرف نظر شود) و فقط در راستای عمودی پرتاب شود و یا از ارتفاع معینی رها شود با حرکت سقوط آزاد با شتاب ثابت g سروکار داریم(که دربخش قبلی توضیح دادیم)در این صورت با حرکت یک بعدی در راستای عمودی سروکار داریم. ولی دربیشتر مواقع یک جسم تحت زاویه ای با افق(مانندθ)پرتاب می شود به این حرکت ،حرکت پرتابی می گویندحرکت پرتابی یکی از صورت های حرکت است که در دو بعد صورت می گیرد .

۱)سرعت اولیه افقی و عمودی

پرتابه ای(جسم پرتاب شونده) با سرعت اولیه “ V₀ “تحت زاویه اولیه ” “ θ_۰ که با افق می سازد پرتاب می شود(مانند گلوله توپی که تحت زاویه θ شلیک شود) درراستای افقی هیچ نیروئی برآن وارد نمی شود و در راستای قائم شتاب کاهنده (-g=-9.8)برآن واردمی شود برای بررسی حرکت پرتابه می توانیم حرکت جسم را به دوحرکت جداگانه تقسیم کرده و هرکدام را حسب سرعت اولیه و شتاب داده شده بنویسیم.(شکل ۶ )

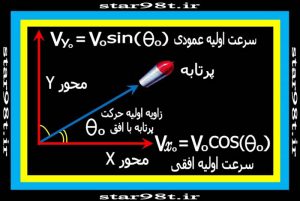
شکل شماره ۶ – تجزیه سرعت اولیه پرتابگربه دو مولفه سرعت عمودی و افقی

۲) معادله افقی حرکت (مسافت پیموده شده )

حرکت در راستای افقی حرکت یکنواخت مستقیم الخط می باشد و شتاب افقی صفر می باشد اگر نقطه  پرتاب را مبدا مختصات بگیریم چون سرعت ثابت است می توانیم بنویسیم .

 

۳)معادله عمودی حرکت

حرکت در راستای عمودی حرکتی است شتابدار که در موقع صعود شتاب کاهنده و در موقع سقوط شتاب افزاینده می باشد . بنابراین می توانیم معادله حرکت را به این صورت بنویسیم .

نکته : جهت محور Y را رو به بالا مثبت و رو به پائین منفی می گیریم در این صورت شتاب همیشه منفی (چه کاهنده و چه افزاینده باشد)وسرعت وقتی روبه بالا است مثبت و وقتی رو به پائین باشدمنفی می شود.  

۴)رابطه بین سرعت عمودی و سرعت افقی(معادله کلی حرکت پرتابی)

در حرکت یک پرتابه معادله حرکت در امتداد عمودی را جداگانه و معادله افقی را هم به صورت جداگانه می نویسیم همچنان که دیده می شود زمان در هردو مشترک می باشد می توانیم زمان را بین دو معادله حذف کرده و مقدار y را بر حسب x بنویسیم مراحل این کار به این صورت است  :
ابتدا معادله حرکت را در راستای x می نویسیم .

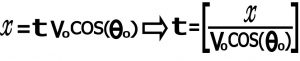
در معادله حرکت در راستای عمودی به جای t مقداری که برحسب x بدست آوردیم قرار می دهیم . و بعد از ساده کردن می توانیم بنویسیم :

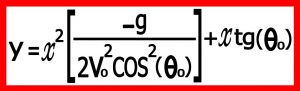
با دقت در معادله بدست آمده متوجه می شویم که این یک معادله “سهمی قائم “ می باشد. بنابراین مسیر یک حرکت پرتابی به شکل سهمی قائم می باشد.( معادله سهمی قائم y=ax²+bx+c )
نکته : سهمی یکی از مقاطع مخروطی می باشد . برای مطالعه در مورد مقاطع مخروطی و معادله آنها به مقاله های “مقاطع مخروطی “ و “ معادله مقاطع مخروطی “ مراجعه کنید .

۵)مسیر حرکت پرتابه

وقتی یک  پرتابه از روی زمین با زاویه θ_۰ پرتاب می شود شروع به اوج گرفتن می کند چون شتاب عمودی منفی (-g) می باشد هر لحظه از سرعت عمودی کاسته می شود (این درحالی است که سرعت افقی ثابت می باشد“V₀cos(θ_۰)” ) تا به بالاترین نقطه مسیر برسدبعد از آن شروع به سقوط می کندو قرینه همان مسیری را که در موقع بالارفتن پیموده درموقع پائین آمدن هم می پیماید تا به زمین برخورد کندبنابراین همانطور که درقسمت قبل دیدیم مسیرسهمی شکلی را طی می کندکه دربالاترین نقطه(نقطه اوج) راس سهمی می باشد.(شکل شماره ۷)همچنین سه مقدار مهم درحرکت پرتابه (نقطه اوج ،مدت زمان و برد) را درقسمت های بعدجدا جدا بدست می آوریم .

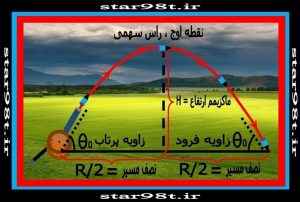
شکل شماره ۷ – پرتاب یک پرتابه در دشت

۶)حداکثر ارتفاع پرتابه H( نقطه اوج )

همانطور که دیدیم مسیر حرکت پرتابه سهمی قائم بوده که راس سهمی نقطه اوج حرکت پرتابه می باشد. در این نقطه ارتفاع ماکزیمم است و سرعت عمودی صفر می باشد.با استفاده از معادلات حرکت شتابدار و با توجه به این که سرعت عمودی در این لحظه صفر است اوج حرکت پرتابه را بدست می آوریم .

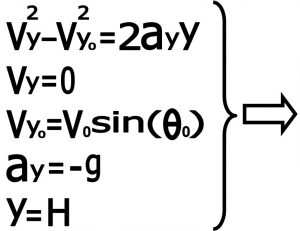
۷)مدت زمان پرواز T

اگر مدت کل زمانی که پرتابه به نقطه اوج می رسد را t فرض کنیم به علت تقارن همین مدت زمان هم طول می کشد تا پرتابه به زمین برگردد و سقوط کند بنابراین زمان کل پرواز را اگر T فرض کنیم دو برابر زمان رسیدن به نقطه اوج می باشد . با استفاده  از معادلات قبل می توانیم بنویسیم .

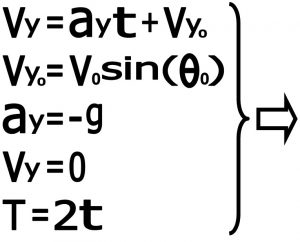
۸) برد پرتابه R

برد پرتابه مسیری است که پرتابه در روی زمین طی می کند یعنی فاصله بین محل پرتاب تا محل سقوط

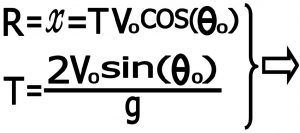
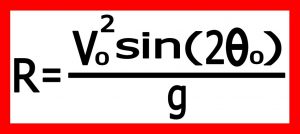
۹) حالت های مختلف حرکات پرتابی

حالت های گفته شده ساده ترین شکل یک حرکت پرتابی می باشد یعنی پرتابه در یک دشت صاف و بدون ارتفاع با زاویه θ_۰ (نسبت به افق) شلیک شده و ما با استفاده از فرمول های فوق حرکت بعدی آن را پیش بینی می کنیم ولی در عمل حالت های مختلفی وجود دارد مانند این که محل پرتاب پرتابه با محل فرود اختلاف سطح داشته باشد (بالاتر یا پائین تر) و یا پرتابه از یک ارتفاع به صورت افقی پرتاب شود (مانند شلیک مستقیم و افقی گلوله) و یا از بالا به پائین با زاویه زیر افق گلوله ای شلیک شود و… در تمام این حالت ها برای حل مسئله ابتدا فقط حرکت عمودی را در نظر گرفته و زمان رسیدن به نقطه اوج را بدست آورده و از روی زمان و معادله افقی حرکت برد پرتابه را بدست بیاورید .
در  مقاله “حل مسائل سینماتیک” در باره همه حالت ها توضیح کامل تر می دهیم .

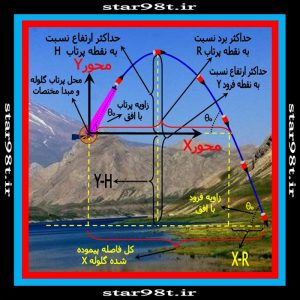
شکل شماره ۸ – اختلاف سطح محل پرتاب پرتابه با محل فرود

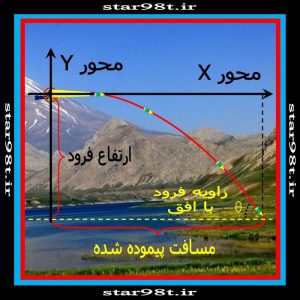
شکل شماره ۹ – پرتاب افقی پرتابه از ارتفاع

شکل شماره ۱۰ – پرتاب بمب از هواپیمای بمب افکن

۱۰)نکاتی در مورد حل مسائل حرکات پرتابی  

مسائل مربوط به حرکات پرتابی به ظرافت های خاص خودش نیاز دارد در مقاله  “حل مسائل سینماتیک” به طور مفصل روش های حل  مسائل را بررسی  می کنیم و مثال های مختلفی می زنیم در این قسمت فقط به چند نکته به طور خلاصه اشاره می کنیم . به طور کلی برای حل مسائل مربوط به حرکت دو بعدی که حرکات پرتابی یکی از این نوع حرکت هاست کافی  است به چند نکته توجه کنیم .
۱۰-۱)تعیین مبدا مختصات : محل پرتاب را مبدا مختصات بگیرید .
۱۰-۲)محورهای مختصات : محورX را در راستای حرکت افقی و محور Yرادر راستای حرکت عمودی بگیرید. 
۱۰-۳) تعیین سرعت اولیه : سرعت اولیه داده شده را به دو مولفه عمودی و افقی تقسیم کرده و آنها را جداگانه از روی کشیدن شکل و با توجه به نسبت های مثلثاتی زاویه پرتاب محاسبه کنید .(فرمول های x=V₀cos(θ_۰) و y=V₀sin(θ_۰) تنها حالت های خاص را شامل می شوند)
۱۰-۴)نوشتن معادلات حرکت:معادلات حرکت را در راستای محور X(محور افقی) و محور Y(محور عمودی ) نوشته و آنها را به طورجداگانه مورد بررسی قرار دهید.(فرمول های قسمت ۲ تا ۴ تنها حالت خاصی از حرکات پرتابی را شامل می شود برای مواردی مانند شکل های۷تا ۹ باید مجدد فرمول ها را بدست آورید)
۱۰-۵)تعیین علامت کمیت ها : علامت کمیت های سرعت و شتاب و مسافت (که هرسه برداری هستند)را با توجه به جهت محور بدست بیاورید با این حساب مثلا مقدار g چون همیشه رو به پائین است همیشه منفی می باشد و سرعت وقتی رو به بالا باشد مثبت و وقتی رو به پائین باشد منفی می شود . و ارتفاع های پائین تراز نقطه پرتاب هم باید منفی بدست بیاید .
۱۰-۶) ارتباط میان حرکت افقی و عمودی : با وجودی که حرکت را در دو راستای عمودی و افقی در نظر گرفتیم و آنها را جداگانه بررسی کردیم ولی زمان در هر دو حرکت مشترک می باشد و به این وسیله می توانیم بین حرکت افقی و عمودی ارتباط برقرار کنیم .

۱۱) حدکثربرد پرتابه

با استفاده از همین فرمول برد پرتابه می توان ثابت کرد که اگر یک پرتابه با سرعت اولیه مشخص و ثابتی تحت زاویه های مختلف پرتاب شود بیشترین برد را زمانی بدست خواهد آورد که تحت زاویه ۴۵درجه پرتاب شود همچنین زاویه هائی که فاصله آنها از ۴۵درجه یکسان باشند برد یکسان و ارتفاع متفاوت دارند.(مثلا پرتابه ای که با زاویه ۳۰درجه پرتاب شود با پرتابه ای که با زاویه ۶۰درجه پرتاب شود برد یکسانی خواهدداشت ( شکل شماره ۱۱) چون اختلاف آنها از ۴۵درجه یکسان است(۶۰-۴۵=۴۵-۳۰=۱۵ ) ولی در زاویه های کمتر پرتابه ازاتفاع کمتر و مدت زمان کمتری را دارا می باشد. (به عنوان یک تمرین موارد فوق را ثابت کنید)

۱۲) اثر مقاومت هوا برحرکت پرتابه

مسائلی که تا این موقع درموردحرکت پرتابی پیش کشیدیم با این فرض بود که از مقاومت هوا صرف نظرکنیم درحالی که همه می دانیم که در روی زمین هوا وجود دارد و هرچقدر سرعت جسمی بیشتر باشدمقاومت هوا هم بیشتر است با آن که گلوله های توپ و تفنگ به گونه ای طراحی شده اند که کمترین مقاومت را در مقابل هوا داشته باشند ولی بخاطر سرعت بسیار زیاد آنها مقاوت هوا بشدت زیاد است به گونه ای که گلوله تفنگی که با سرعت ۸۰۰ متردرثانیه و تحت زاویه ۴۵درجه شلیک می شود باید ۶۵کیلومتر بپیماید (محاسبه مربوط را انجام دهید) درحالی که حداکثر برد نهائی این سلاح ها (مانند اسلحه ژ۳)۳۵۰۰متر(حدود ۲۰برابر کمتر) می باشد . محاسبه اثر نیروی مقاومت هوا بر اشیائی که درهوا حرکت می کنند پیچیده بوده و در این مقاله نمی گنجد و در مقاله های بعد در این مورد توضیح بیشتر خواهیم داد .

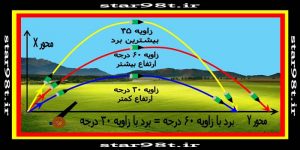
شکل شماره ۱۱ – پرتاب یک پرتابه تحت زوایای مختلف

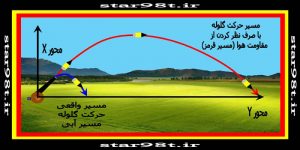
شکل شماره ۱۲ – پرتاب یک پرتابه در حضور هوا و بدون حضور هوا

۶- مکانیک دورانی

در بخش های قبلی فرمول ها و معادلات حرکت انتقالی شتابدار را توضیح دادیم و بعد حرکت در دو بعد(حرکت در صفحه مانند حرکت پرتابی) را مورد بررسی قرار دادیم در تمام آن موارداجسام مورد نظر را به صورت یک نقطه (مرکز جرم)در نظر گرفتیم و جابجائی کل جسم(حرکت مرکز جرم) را به صورت حرکت یک نقطه مورد بررسی قرار دادیم . در این بخش در مورد جابجائی کل اجسام صحبت نمی کنیم همچنین نمی توانیم جسم را به صورت ذره در نظر بگیریم بلکه در مورد چرخش یک جسم صلب(جسم صلب یا جسم سخت ،جسمی است که همه اجزاء آن در حین حرکت انتقالی و یا دورانی پیوستگی خود را حفظ می کنند) به دور نقطه ای به نام مرکز دوران صحبت می کنیم . چنین حرکتی را حرکت دورانی می نامند و همچنان که در حرکت انتقالی حرکت می تواند مستقیم الخط و یا در صفحه و یا در فضا باشد حرکت دورانی هم می تواند حول یک محور یا همزمان دو و سه محور باشد که ما دراینجا  فعلا حرکت دور یک محور را بررسی می کنیم . 

۱)مکانیک دورانی چیست ؟

دَوَران، حرکت یک جسم در جهت دایره‌ای است. در دوران همه اجرای یک جسم صلب به دور یک محور به نام محور دَوَران می چرخند. بررسی این نوع حرکت مکانیکی را پدید آورده که به نام مکانیک دورانی نامیده می شود . و مانند مکانیک انتقالی می توان آن را به “سینماتیک دورانی” و “دینامیک دورانی“  تقسیم کرد.
وقتی کمیت های دوران را بدون علت آن بررسی می کنیم با سینماتیک دورانی سروکار داریم و وقتی به علت های دوران می پردازیم با دینامیک دورانی سروکار داریم . 

۲)تفاوت مکانیک دورانی و مکانیک انتقالی

در انتقال کامل یک جسم (حرکت جسم)باحرکت انتقالی سرو کار داریم در حالی که در چرخش یک جسم دور یک محور با مکانیک دورانی سروکار داریم . در مکانیک انتقالی با کمیت هائی مانند (سرعت و شتاب و جرم و…نیرو )سرو کار داریم . در حالی که در مکانیک دورانی با کمیت هائی مانند (سرعت زاویه ای و شتاب زاویه ای و…گشتاور ) سروکار داریم .

۳) شباهت های مکانیک انتقالی و مکانیک دورانی

 کمیت ها و فرمول های مکانیک دورانی اگر چه از بسیاری از جهت با مکانیک انتقالی تفاوت دارند ولی روابط بین آنها بسیار شبیه مکانیک انتقالی  می باشد در واقع یک تناظر یک به یک بین کمیت های حرکت دورانی با حرکت انتقالی وجود دارد به عنوان مثال: “سرعت درمکانیک انتقالی با سرعت زاویه ای درمکانیک دورانی“، “شتاب درمکانیک انتقالی با شتاب زاویه ای در مکانیک دورانی “

۴) بردار یا اسکالر

بسیاری از کمیت های در مکانیک انتقالی (مانند مسافت و سرعت و شتاب) ماهیت برداری دارند . در مکانیک  دورانی می توانیم کمیت هائی مانند جابجائی زاویه ای و سرعت زاویه ای و …را هم اسکالر و هم بردار در نظر بگیریم که ما در این بخش بخاطر سادگی همه را اسکالر در نظر می گیریم .
تذکر مهم : کمیت هائی که هم اندازه و هم جهت دارند کمیت های برداری و کمیت هائی که فقط اندازه دارندکمیت های اسکالر نامیده می شوند . جهت آشنائی بیشتر با بردارها به مقاله”بردارها “مراجعه کنید. 

۷-سینماتیک دورانی

در بخش قبلی در مورد مکانیک دورانی توضیح دادیم و گفتیم مکانیک دورانی مانند مکانیک انتقالی به دو قسمت سینماتیک دورانی و دینامیک دورانی تقسیم می شود در این بخش در مورد سینماتیک دورانی توضیح می دهیم و در مقاله “دینامیک “ در مورد دینامیک دورانی توضیح می دهیم .

۱) زاویه به جای مسافت   

در مکانیک انتقالی می توانستیم حرکت همه اجزاء جسم را حرکت نقطه ای به عنوان مرکز جرم در نظر گرفته و همچنین درحرکت انتقالی مستقیم الخط یک نقطه به نام مبدا را روی خط راست تعیین کرده و سمت راست را حرکت درجهت مثبت و سمت چپ را درجهت منفی درنظر بگیریم(درصفحه ودرفضای سه بعدی مبدا مختصات تعیین کرده و جهت ها را بر اساس مبدا مختصات تعیین کنیم .)
ولی در حرکت دورانی چون همه اجزاء جسم با سرعت های متفاوت حول مرکز دوران می چرخند (نقاط دورتر باسرعت کمتر و نقاط نزدیکتر با سرعت بیشتر) ما نمی توانیم حرکت جسم را حرکت مرکز جرم در نظر بگیریم همچنین بعلت تفاوت سرعت انتقالی نقاط مختلف جسم، از سرعت انتقالی هم نمی توانیم استفاده کنیم با این وجود نقاط مختلف جسم همگی زاویه های یکسانی را در زمان های یکسان طی می کنند از همین واقعیت می توانیم کمیت جدیدی تعریف کرده و به جای مسافت طی شده قرار دهیم و آن زاویه پیموده شده می باشد بنابراین در حرکت دورانی به جای مسافت طی شده می توانیم از زاویه طی شده (زاویه ای که جسم دوار طی کرده  است) استفاده کنیم.زاویه طی شده در مکانیک دورانی را با ”θ”(تتا)نمایش می دهیم. واحد زاویه در سیستم SI رادیان (rad)می باشد (اگر چه در ریاضیات و علوم مختلف ترجیح داده می شود که ازدرجه و اجزای آن همچون دقیقه و ثانیه استفاده کنند)

۲)سرعت زاویه ای به جای سرعت خطی

همچنان که گفتیم چون درحرکت دورانی همه اجزائ جسم با سرعت یکسانی جابجا نمی شوند پس نمی توانیم از سرعت انتقالی استفاده کنیم درحرکت زاویه ای به جای مسافت طی شده زاویه طی شده راجایگزین کردیم بنابراین در حرکت زاویه ای می توانیم “سرعت زاویه ای” را جایگزین سرعت انتقالی کنیم بنابر تعریف :
 « زاویه پیموده شده در واحد زمان را سرعت زاویه ای(angular velocity)  می نامند »
بنابراین در سینماتیک انتقالی مسافت پیموده  شده در واحد زمان را سرعت و در سینماتیک دورانی زاویه پیموده شده در واحد زمان را سرعت زاویه ای می نامند. سرعت زاویه ای را با امگا(ω)نشان داده و واحد آن درسیستم SI “رادیان بر ثانیه(rad/s)  می باشد هرچند واحدهای دیگری مانند درجه بر ثانیه یا دقیقه بر ثانیه هم استفاده می شود .

 

نکته : ازنظر دیمانسیون یا معادله ابعادی زاویه بدون دیمانسیون می باشد بنابراین دیمانسیون (ω) یا سرعت زاویه ای را می توان به صورت “ T^-1 “نوشت .

۳)سرعت زاویه ای بردار یا اسکالر ؟

در بسیاری از مسائل برای سادگی کار سرعت زاویه ای را کمیتی اسکالر در نظر می گیرند. در این حالت اگر جهت گردش پادساعتگرد (خلاف عقربه های ساعت) باشد سرعت زاویه ای را عددی مثبت و اگر درجهت عقربه های ساعت باشد سرعت زاویه ای منفی می شود. (شکل شماره ۱۳)
سرعت زاویه ای کمیتی برداری می باشد که علاوه براندازه جهت نیزداردجهت بردار سرعت زاویه ای بر صفحه چرخش عمود بوده و از قاعده دست راست تعیین می شود .

شکل شماره ۱۳ -حرکت دورانی و جهت چرخش آن

۴) سرعت دورانی

وقتی سرعت زاویه ای بالا باشد و جسم درهر ثانیه جندین دور بچرخد به جای سرعت زاویه ای از سرعت دورانی استفاده می کنند. از این رو گاهی از اوقات سرعت زاویه ای را سرعت دورانی نیز می نامند که در این صورت واحد آن را بجای واحدهای سرعت زاویه ای(رادیان بر ثانیه یا درجه بر ثانیه و…)برحسب تعداد دورهای زده شده در واحدزمان تعیین می کنند مانند : دور دردقیقه (r/min)، دور برثانیه (r/s) و…که البته یکای اصلی SI نیست و بیشتر در ماشین های دوار مورد استفاده می شود( مانند عقربه های دور موتور ماشین که تعداد دورهائی که موتور ماشین در یک دقیقه می زند را نشان می دهد . (شکل های شماره  ۱۴ تا ۱۶ )

شکل های شماره ۱۴ تا ۱۶ – نمونه ای از عقربه های دور موتور در خودرو

نکته: دوردردقیقهRevolutions Per Minute))به اختصارRPMنامیده می شود این یکا، بیان‌کنندهٔ تعداد دورهای چرخشی کاملی است که یک قطعه در مدت یک دقیقه به دور یک محور ثابت انجام می‌دهد. بنابراین هر RPM یک دور بر دقیقه حساب شده که بر حسب رادیان بر ثانیه برابر می باشد با :  

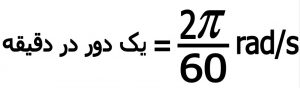
۵) شتاب زاویه ای

شتاب زاویه ای متناظر شتاب خطی است و عبارت است از مقدار تعغیر سرعت زاویه ای در واحد زمان که با “f” ( آلفا ) نمایش می دهند. واحداصلی شتاب زاویه ای “رادیان بر مجذور ثانیه “ (rad/S²)هم می باشد ولی از واحدهای دیگری مانند درجه بر مجذور ثانیه یا دور بر مجذور ثانیه و… هم استفاده می کنند.  

۶) سرعت زاویه ای متوسط و سرعت زاویه ای لحظه ای

همان تعریف ها که در مورد سرعت متوسط انتقالی و سرعت لحظه ای انتقالی کردیم در مورد سرعت زاویه ای هم تعریف می شود .
۱-۶) سرعت زاویه ای متوسط :  سرعت زاویه ای متوسط عبارت است از کل زاویه ای طی شده در مدت زمانی است که این زاویه طی شده است بنابراین برای جسمی که حرکت دورانی رفت و برگشت انجام می دهد این سرعت صفر می باشد .
۲-۶) سرعت زاویه ای لحظه ای : سرعت لحظه ای دورانی سرعتی است که متحرک در هر لحظه دارد و یا به عبارتی سرعتی است که در هر لحظه عقربه دور ماشین نشان می دهد . همچنین می توانیم سرعت زاویه ای لحظه ای را مشتق زاویه طی شده نسبت به زمان حساب کنیم .

۸- رابطه بین حرکت انتقالی با حرکت دورانی

علی رغم اختلاف بین پارامترهای حرکت انتقالی و دورانی که در بخش های قبلی توضیح دادیم شباهت های بسیاری هم بین این دو نوع حرکت وجود دارد دورانی و پارامترهای حرکت دورانی و حرکت زاویه ای شباهت بسیار زیادی به هم دارند در این بخش در مورد این شباهت ها توضیح می دهیم .

۱)تناظر یک به یک بین حرکت انتقالی و حرکت دورانی

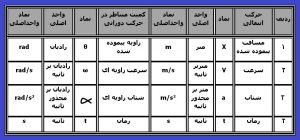
درحرکت انتقالی شتابدار ما با چهار متغیر روبر هستیم (مسافت x ،سرعتV ، شتاب aزمانt) که روابط بین آنها را در جدول شماره یک گرد آوری کردیم .(بخش سوم – سینماتیک انتقالی-معادلات حرکت مستقیم الخط) بین هر کدام ازمتغیرهای حرکت انتقالی و حرکت دورانی (زاویه پیموده شده θ، سرعت زاویه ای ω، شتاب زاویه ای آلفا و زمانt )یک تناظر یک به یک وجود دارد (جدول شماره ۳ )

جدول شماره ۳ – تناظر یک به یک بین متغیرهای حرکت انتقالی و دورانی

۲) شباهت جدول حرکت انتقالی و حرکت دورانی

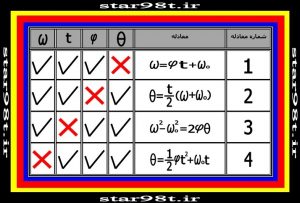
در جدول شماره یک روابط بین متغیرهای حرکت انتقالی را جمع آوری کردیم نظر به شباهت بسیار زیادی که بین متغیرهای حرکت انتقالی با حرکت دورانی وجود دارد همبن فرمول ها و همین جدول را هم می توانی برای حرکت دورانی درست کنیم که روش ها و راه بدست آوردن آن همان است که در حرکت انتقالی توضیح دادیم از این رو در اینجا دیگر توضیح نمی دهیم .

جدول شماره ۴ – فرمول های چهار گانه حرکت شتابدار دورانی

     ۳) رابطه بین مسافت طی شده و زاویه طی شده ، سرعت انتقالی و سرعت دورانی

حال حرکت دورانی را از جهت دیگر بررسی می کنیم . در قسمت های مختلف این بخش حرکت دورانی را مستقل از حرکت انتقالی شرح دادیم . برای این کار جسم دوران کننده را یکپارچه فرض کرده و متغیرهای حرکت دورانی را مستقل از حرکت انتقالی و برای تمام نقاط جسم دوران کننده به صورت یکسان تعریف کرده و روابط آن ها را بدست آوردیم .
در این قسمت هر نقطه را جداگانه بررسی کرده و حرکت انتقالی آن را به صورت مستقل بدست می آوریم .

برای این کار فرض می کنیم فاصله نقطه ای از مرکز دوران “r” باشد و این نقطه در مدت زمان “t” زاویه” “θ را می پیماید برای بدست آوردن مسیر پیموده شده خیلی ساده زاویه پیموده شده را در r ضرب می کنیم . به همین ترتیب سرعت انتقالی نقطه را هم از ضرب کردن سرعت زاویه ای در r بدست می آوریم در مورد شتاب در قسمت بعد توضیح می دهیم .

  

۴) رابطه بین شتاب زاویه ای و شتاب انتقالی

جسمی که روی یک مسیر دایره ای حرکت می کند دارای دو نوع شتاب می باشد یکی شتاب در راستای حرکت بوده که شتاب مماسی می نامندو با “a_T” نمایش می دهند و دیگری شتاب عمود بر مسیر حرکت و به طرف مرکز دوران می باشد که شتاب مرکز گرا نامیده شده و با “a_R” نمایش می دهند رابطه بین شتاب های مماسی و شتاب زاویه ای و فاصله نقطه از مرکز دوران ،همچنین شتاب مرکز گرا فاصله از مرکز دوران به این صورت می باشد . که در ادامه بدست می آوریم .
۴-۱) رابطه بین شتاب مماسی و شتاب زاویه ای : شتاب مماسی مقدار افزایش سرعت انتقالی نقاط در حال چرخش می باشد و رابطه آن با شتاب زاویه ای شبیه همان رابطه بین سرعت انتقالی و سرعت دورانی می باشد .
۴-۲)محاسبه شتاب مرکز گرا بر حسب سرعت زاویه ای : همانطور که در بخش چهارم همین مقاله“ ۴- حرکت چند بعدی “ توضیح دادیم برای ذره ای که بر گرد یک دایره می چرخد حتی اگر سرعت از نظر اندازه تعغیر نکند چون از نظر جهت تعغیر می کند و سرعت یک کمیت برداری می باشد شتاب ایجاد می شود ولی  چون عمود بر مسیرحرکت می باشد نمی تواند سرعت انتقالی(و همینطور سرعت زاویه ای)را تعغیردهد. در همان جا ما مقدار این شتاب(شتاب مرکزگرا) را برحسب سرعت خطی بدست آوردیم و در اینجا شتاب مرکزگرا را برحسب سرعت زاویه ای بدست می آوریم .

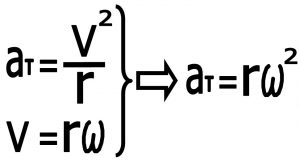
بنابراین به صورت خلاصه رابطه بین شتاب مرکز گرا و سرعت زاویه ای و سرعت خطی از این قرار می باشد .

 

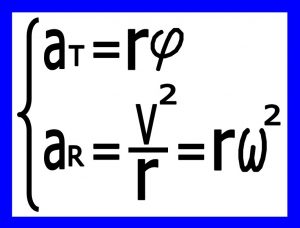
برای مطالعه سایر مقاله های نجومی روی شکل زیر کلیک کنید.

برای مطالعه مقاله های روانشناسی اینجا  را کلیک کنید .

عکس های طبیعت, طبیعت خوانسار , شکوفه های بهاری  , گلستان کوه ,دانلود آلبوم های کامل بهترین و زیباترین عکس ها ,آلبوم هائی با صدها عکس کیفیت بالا ,  در هیچ کجای اینترنت این عکسها را پیدا نمیکنید , عکس هابدون استفاده از تکنیک های فتوشاپ تهیه شده , کاملا طبیعی 

برای آموزش کامل و حرفه ای گوگل مپ روی شکل زیر کلیک کنید

همه جیز در مورد گوگل مپ

۱) هر گونه اظهار نظر را در فرم اظهار نظر کاربران وارد کنید .
۲) نظرات بعد از تایید مدیریت نشان داده می شود .
۳) با انتقادات و پیشنهادات سازنده خود ما را هرچه بیشتر  همراهی کنید . مدیریت از انتقادات و پیشنهادات سازنده شما استقبال میکند .
۴) نوشته های قرمز پر رنگ ارجاع به لینک هستند که هنوز لینک آنها قرار داده نشده است ( هنوز صفحه آنها منتشر نشده است )
۵) نوشته های آبی پر رنگ ارجاع به لینک هستند که لینک آنها قرار داده شده است ( صفحه آنها منتشر شده است )
۶) هرگونه بهره برداری : کپی تمام و یا قسمتی از مطالب این سایت بدون ارجاع منبع آن ممنوع می باشد .
۷) تکثیر فایل های Pdf با ذکر منبع آزاد ولی فروش آن تحت هر عنوان و با ذکر منبع هم ممنوع می باشد.