دوره تناوب و فاصله ماه تا زمین

در این بخش  به پدیده هائی در ارتباط با گردش ماه به دور زمین می پردازیم .

۱- مرکز جرم زمین و ماه

 بسیاری گمان می کنند که کره ماه در مداری بیضی به دور زمین می چرخد ولی در واقع این مجموعه ماه و زمین است که هر کدام در مدار جداگانه به دور مرکز جرم مشترکشان می چرخند و این مرکز جرم در مرکز زمین نیست . بلکه نقطه ای است در ۴۷۰۰ کیلومتری از مرکز زمین که اگر چه در داخل زمین قرار دارد ولی در مرکز زمین نیست . ( شکل شماره ۱ )

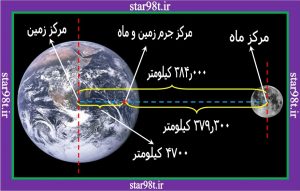
شکل شماره ۱ -مرکز جرم زمین و ماه

ماه و زمین هر دو دور مرکز جرم مشترکشان می چرخند و این مرکز جرم حول خورشید می چرخد . بنابر این زمین در مدار خود به دور خورشید  همزمان دور مرکز جرم مشترک خود با ماه هم می چرخد و یک مسیر زیگزاگی ( موجی را در فضا طی می کند ) همچنین ماه هم علاوه بر گردش به دور مرکز جرم مشترک زمین و ماه به دور خورشید هم در یک مدار زیگزاگی می چرخد .(شکل شماره ۲ )

شکل شماره ۲ – حرکت زیگزاگی زمین در مدارش به دور خورشید

نکته : با توجه به فاصله مرکززمین از مرکز جرم  مجموعه ماه و زمین (۴۷۰۰ کیلومتر) و مدار زمین به دور خورشید(۰۰۰ر۰۰۰ر۱۵۰کیلومتر ) موج زیزاگ ها در این شکل بسیار اغراق آمیز است

۲- دوره تناوب ماه

قبل از این که در مورد دوره تناوب ماه شرح دهیم در مورد تفاوت رصد از روی زمین و فضا توضیحاتی می دهیم

۱ ) تفاوت رصد از روی زمین و فضا

دوره گردش زمین به دور خود (حرکت وضعی)و یا دوره تناوب حرکت ماه به دور زمین و یا سیارات به دور خورشید و… را باید از دو منظر نگاه کرد :
۱-۱) از منظر ناظر روی زمین :  در این حالت ناظر ما روی زمین قرار دارد و آسمان را آنگونه که از روی زمین دیده می شود نظاره می کند .
۲-۱) از منظر ناظر دور دست خارج از زمین : این حالت بستگی دارد به این که چه چیزی را می خواهیم رصد کنیم . در صورتی که مجموعه زمین و ماه باشد ناظر باید خارج از مجموعه زمین و ماه باشد و در صورتی که زمین و خورشید باشد ناظر باید خارج از مجموعه زمین و خورشید باشد و…
در هر صورت رصد در روی زمین ( همچنین داخل مجموعه ای که می خواهیم رصد کنیم ) با آنچه در فضا رصد می شود با هم تفاوت دارد ( خارج از مجموعه ای که می خواهیم رصد کنیم )
۳-۱) تفاوت رصد در داخل مجموعه و خارج از مجموعه : رصد از روی زمین ( و حتی داخل مجموعه ای که می خواهیم رصد کنیم ) با آنچه در خارج از مجموعه رصد می شود با هم تفاوت دارد عدم توجه به این مسئله باعث خطاهای فاحش و اشتباه در نتایج رصد می شود .
به عنوان مثال : شبانه روز زمینی را اگر نسبت به ستاره های دور دست نگاه کنیم مقدار ۲۳ ساعت و ۵۶ دقیقه بدست می آوریم ( در این حالت می توانیم تصور کنیم ناظر خارج از مجموعه زمین و خورشید است )در حالی که اگر نسبت به خورشید بسنجیم ۲۴ ساعت می شود . (در این حالت ناظر در روی زمین می باشد )
 مقاله روز نجومی و روز خورشیدی  را از همین سایت مطالعه کنید .

۲) دوره تناوب هلالی و دوره تناوب نجومی چیست ؟ 

دوره تناوب ماه زمان چرخش ماه به دور زمین می باشد و دوره تناوب سیارات زمان گردش یک دور کامل سیاره به دور خورشید می باشد . ولی چون زمین به دور خورشید حرکت می کند اگر از روی زمین رصد کنیم با آنچه از خارج از منظومه شمسی رصد می شود با هم تفاوت می کند بنابر این دو گونه دوره تناوب تعریف می کنیم ( این تعریف شامل حرکت سیارات به دور خورشید و همچنین گردش ماه به دور زمین می شود )
۲-۱ ) دوره تناوب نجومی : مدت زمانی که سیاره یک دور کامل به دور خورشید بچرخد که به این دوره تناوب سال نجومی هم می گویند . در مورد ماه دوره تناوبی است که ماه یک دور کامل به دور زمین بچرخد . برای رصد و بدست آوردن دوره تناوب باید رصد نسبت به ستارگان دوردست انجام شود در این صورت در روی زمین هم می توانیم دوره تناوب را بدست آوریم . بنابر این برای بدست آوردن دوره تناوب نجومی ماه موقعی که ماه مقابل یکی از ستارگان دوردست قرار دارد در نظر می گیریم بعلت حرکت ماه در مدارش ماه از مقابل ستاره کنار می رود در شب های بعد ماه را رصد می کنیم تا دوباره مقابل همان ستاره قرار بگیرد مدت زمان گذشته دوره تناوب نجومی ماه و زمانی است که ماه یک دور در مدارش به دور زمین می چرخد .
روش بدست آوردن دوره تناوب نجومی و هلالی سیارات تفاوت دارد که در جای خود توضیح می دهیم .

۲-۲ ) دوره تناوب هلالی : اگر ما یکی از  اهله ماه(ماه نو , هلال افزاینده و… ماه بدر و…هلال کاهنده) را در نظر بگیریم مثلا ماه کامل (بدر) و بعد دوباره صبر کنیم تا ماه کامل شود این مدت دوره تناوب هلالی نامیده میشود .

۳) علت تفاوت دوره تناوب هلالی و نجومی ماه  

زمان یک بار گردش ماه به دور زمین دوره تناوب نجومی(Astrological month) نام دارد .ولی آنطور که از زمین دیده و رصد می شود دوره تناوب هلالی (Crescent moon)نام دارد . دوره تناوب نجومی ماه را نسبت به یک ستاره ثابت می سنجیم در حالی دوره تناوب هلالی را زمان ماه کامل(بدر) تا ماه کامل(بدر) بعدی که این دو با هم فرق دارند. دوره تناوب نجومی ماه حدود ۲۷/۳روز (۲۷/۳۲۱۶۶روز) می باشد در حالی که دوره تناوب هلالی ۲۹/۵روز (۲۹/۵۳۰۵۹روز) می باشد . یعنی ما از بدر تا بدر بعدی و یا از ماه نو تا ماه نو بعدی (یعنی یک ماه قمری) را ۲۹/۵روز اندازه می گیریم در حالی که زمان یک دور گردش ماه به دور زمین ۲۷/۳ روز می شود .
حال به شکل شماره ۱۲ نگاه کنید . همانطور که در شکل ها دیده می شود علت این اختلاف این است که کره ماه در مدتی که طول می کشد یک دور به دور زمین بچرخد همراه زمین در گردش به دور خورشید شرکت می کند در حقیقت در این زمان ماه به همراه زمین به اندازه تقریبی ۲۷درجه در مسیرحرکت به دور خورشید چرخیده و خط واصلی که زمین را به خورشید وصل می کند دیگر از ماه نمی گذرد (مقابله) و بنابر این ماه باید به اندازه ۲۷درجه اضافی دور زمین بچرخد تا دوباره به حالت مقابله برسد و این به اندازه ۲/۲ روز زمان می برد .
نکته۱ :در مدتی که ماه باید دور زمین بچرخد تا جبران ۲۷درجه را بکند باز هم زمین به حرکتش به دورخورشید ادامه می دهد و به زمان اضافی افزوده  می شود ولی در مجموع زمان اضافی۲/۲روز می شود .  

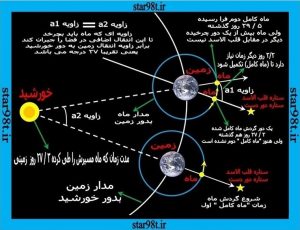
شکل شماره ۳ – تفاوت دوره تناوب نجومی و هلالی

۴) آنچه رصد گر زمینی می بیند 

آنچه رصدگر زمینی موقع رصد ماه مشاهده می کند به این صورت است :
۱- ۴) اولین روز : موقع ماه کامل (بدر) ستاره پر نوری مانند قلب العقرب را درست بالای ماه در نظر می گیریم .

شکل شماره  ۴- شروع روز شماری از بدر ( ماه کامل ) اولین روز

۴-۲) دومین روز بعد از ۲۷/۳ روز  : بعد از گذشت ۲۷/۳ روز دوباره قلب العقرب را بالای ماه می بینیم ولی ماه کامل نیست .

شکل شماره ۵ – بعد از گذشت ۳ / ۲۷ روز ماه به مقابل قلب الاسد رسیده ولی هنوز بدر( ماه کامل ) نشده

۴-۳) سومین روز بعد از ۲۹/۵ روز از اولین روز  : بعد از گذشت ۲/۲ روز ( از دومین روز ) ماه کامل میشود ولی قلب العقرب را دیگر بالای ماه نمی بینیم ستاره از جای خود حرکت کرده و جابجا شده است .

شکل شماره ۶  – بعد از گذشت ۵ / ۲۹ روز ( از اولین روز ) ماه کامل ( بدر ) شده ولی ماه از کنار قلب الاسد گذشته

۳- فاصله ماه تا زمین 

 فاصله ماه از زمین را به روش های مختلف می توان بدست آورد که در اینجا تعدادی از این روش ها را شرح می دهیم .

۱) محاسبه فاصله ماه تا زمین به روش تیکو براهه

این روش نخستین بار به وسیله تیکو براهه بکار برده شد  روش کار به این صورت است که از دو نقطه مختلف دور ازهم در روی زمین,  ماه را رصد کرده و ارتفاع ماه را جداگانه اندازه می گیرند. (شکل ۷)

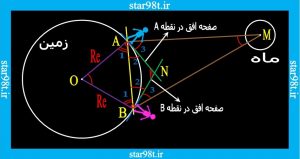
شکل شماره ۷ – محاسبه فاصله ماه تا زمین به روش تیکو براهه

 در  شکل ( شماره ۷ ) از دو نقطه A و B (که مختصات آن را داریم )در یک لحظه مشخص ( یک روز و یک ساعت و دقیقه و ثانیه ) ارتفاع  ماه را اندازه می گیرند . بنابر این داریم 

زاویه A>را به سه قسمتA1>و A2>و A3> تقسیم کرد و زاویه B>را هم به سه قسمت B1>و B2> و B3> تقسیم می کنیم و برای بدست آوردن AM یا BM ( به علت بزرگی فاصله ماه تا زمین نسبت به فاصله AB تقریبا مساوی است ) در نهایت باید اندازه AB و زاویه  ∝ = A2 + < A3> و B2+ < B3 = β> را بدست آوریم

فاصله ماه تا زمین = AM =  BM

۱-۱) بدست آوردن زاویه های A1> و B1>  :

در شکل شماره ۷ در مثلث OAB داریم  :

بنابر این برای بدست آوردن زاویه های A1> و  B1> کافی است زاویه O> را بدست آوریم  . که فرمول آن به این صورت است :

 (کاربرد هندسه و مثلثات کروی در نجوم از همین سایت یا مثلثات کروی و کاربردهای آن )
نکته :  زاویه <Oبرابر است با “اندازه کمان  “ABیعنی فاصله زاویه ای بین دو نقطه A و B

۱-۲) بدست آوردن زاویه های A2> و B2> :

 برای بدست آوردن  زاویه های A2> و  B2>داریم :  

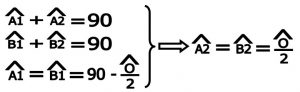
۱-۳) محاسبه زاویه های  ∝ = A2 + < A3> و B2+ < B3 = β :

 با بدست آوردن زاویه های A2> و  B2> داریم :

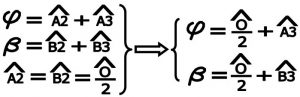
۱-۴ ) محاسبه AB ( فاصله دو نقطه A و  B داخل زمین ) :

در مثلث ABO (شکل شماره ۷ ) رابطه سینوس ها را بکار می بریم

(بدست آوردن اجزاء مجهول مثلث به کمک اجزاء معلوم  در همین سایت مطالعه کنید )

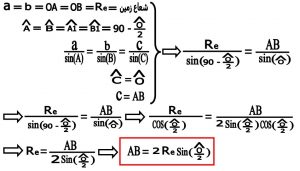
نکته۱ :منظور از:A=<B=<A1=<B1 >و   C= <O> و c=ABجایگزاری برای استفاده دررابطه سینوس ها است .
نکته ۲ : پاره خط AB وتر گذشته از دو نقطه AوB است و این فرمول اندازه وتر است .

۱-۵) محاسبه AM یا AN ( فاصله ماه تا زمین  ) :

در مثلث AMB زاویه های مثلث را حساب می کنیم .

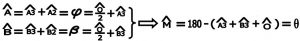
حال مثلث AMB که دو راس A و B محل دو ناظر در روی زمین بوده و M مرکز کره ماه می باشد در نظر گرفته

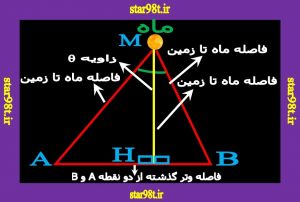
شکل شماره ۸ – مثلث بین دو نقطه زمین و کره ماه

فرمول سینوس ها  را به کار می بریم .

در این فرمول به جای A> زاویه A3> و به جای زاویه B> زاویه B3>و به جای C> زاویه M> را به کار می بریم .
به جای ضلع c  پاره خط AB  و به جای اضلاع a وb  اندازه AM وBMرا می نویسیم 

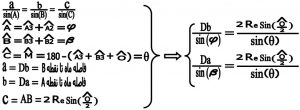
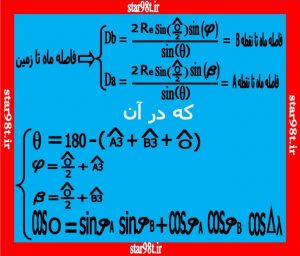
نکته ۱ :  این همان مثلث AMB  شکل شماره ۷ است

نکته ۲: در صورتی که دو نقطه روی یک طول جغرافیائی باشند . O> به صورت خیلی ساده برابر است با اختلاف طول جغرافیائی( یعنی Δλ) بنابر این بهتر است رصددر دو نقطه با طول جغرافیائی یکسان انجام شود .

نکته ۳: فاصله Da و Db تقریبا با هم برابرند ولی در اینجا به صورت جداگانه نوشته شده تا نشان دهیم هر رصد کننده باید جداگانه فاصله ماه از خودش را اندازه بگیرد .  

نکته ۴: در این روش فاصله مرکز ماه تا دو نقطه بدست می آید برای بدست آوردن فاصله تا مرکز زمین شعاع زمین را باید اضافه کرد .  

 ۲)  اختلاف منظر و محاسبه به کمک اختلاف منظر

یکی از راه های اندازه گیری فاصله های زیاد استفاده از  منظر می باشد . روش های  اختلاف منظر روش بسیار کار امد و مفیدی در نجوم می باشد که می توان به وسیله آن فاصله ماه و اجرام سماوی دور دست را بسادگی اندازه گیری کرد و در سایر علوم هم کاربرد گسترده ای دارد .
طبق تعریف جابجا شدن ظاهری یک شیء نسبت به زمینه‌اش که معلول جابجا شدن ناظر باشد را اِختِلافِ مَنظَر یا دیدگشت می‌گویند. ( شکل شماره ۹ )

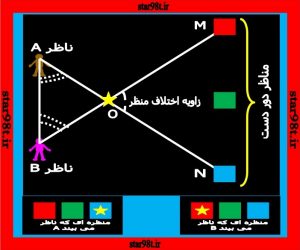
شکل شماره ۹- اختلاف منظر چیست ؟

در شکل شماره ۹ جسم موجود در نقطه O جسم نزدیک می باشد و دو ناظر که در دو نقطه A و B واقع هستند وقتی این جسم را نسبت به نقاط دوردست مقایسه می کنند در دو نقطه جداگانه M و N می بینند .
در این صورت زاویه O زاویه اختلاف منظر نامیده می شود . براحتی می شود این زاویه را بکمک عکسبرداری و اندازه گیری فاصله ستاره های جابجا شده در زمینه آسمان بدست آورد و با داشتن فاصله AB و یا این فرض که مثلث متساوی الساقین بوده و زاویه های A و B هم با هم مساویند . فاصله جسم نزدیکتر را همان AO و BO فرض کرد و از فرمول سینوس ها این فاصله را محاسبه کرد .
بنابر این داریم :

 

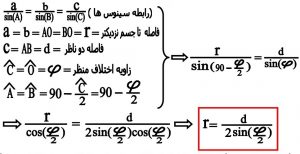
 نکته : در مورد اندازه گیری فاصله ستارگان با استفاده از اختلاف منظر بعلت طولانی بودن فاصله ستارگان  می توانsin(∝/۲) را برابر ۲/∝ ( بر حسب رادیان ) در نظر گرفت که فرمول به این صورت در می آید: 

  

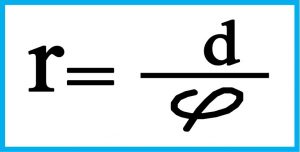
۳) محاسبه فاصله ماه تا زمین با روش اختلاف منظر

برای اندازه گیری فاصله ماه تا زمین به روش اختلاف منظر باید این کارها را انجام دهیم :
۳-۱) عکس گرفتن از هلال ماه : در یک زمان (روز و ساعت و دقیقه و ثانیه ) مشخص و از دو نقطه مشخص ( که مختصات آن معلوم باشد) از ماه عکس می گیریم ( بهتر است در موقع هلال نازک ماه باشد تا ستاره های اطراف در عکس بهتر معلوم شوند)

۳-۲) اندازه گیری زاویه ∝: با مقایسه عکس ها(دستگاهی وجود دارد که هر گونه تفاوت عکس ها و
ابجائی را نشان می دهد و اندازه حرکت جابجائی اجسام جابجا شده را هم نشان می دهد ) زاویه ∝ را بدست می آوریم .

۳-۳) فاصله دو نقطه را حساب می کنیم( مقدار d ) : با داشتن مختصات دو نقطه به روشی که در قسمت (۵-۱ ) شرح داده شد فاصله دو نقطه را در داخل زمین (وتری از زمین که بر دو نقطه می گذرد) را بدست می آوریم  (مقدار d)

۳-۴) بدست آوردن فاصله ماه تا دو نقطه : با استفاده از فرمول قسمت (۲) فاصله ماه را تا ناظر بدست می آوریم .

۳-۵) فاصله مراکز ماه و زمین : به مقدار بدست آمده شعاع زمین را هم اضافه می کنیم .

۴) محاسبه فاصله ماه تا زمین با استفاده از خسوف ( ماه گرفتگی )

خورشید همیشه نصف زمین را روشن می کند و نصف دیگر در تاریکی قرار می گیرد که ما به عنوان شب می شناسیم با این حال سایه زمین به عنوان مخروطی در فضا گسترده شده و حدودا ۱۰۸ برابر قطر زمین یعنی ۶۰۰ر۳۷۵ر۱ کیلومتر می باشد . ( که البته بخاطر بیضی بودن مدار زمین متغیر است از ۰۰۰ر۳۰۰ر۱ تا ۰۰۰ر۴۰۰ر۱ کیلومتر)در موقع خسوف ماه از داخل این مخروط می گذرد با محاسبه زمان های گرفت (از لحظه آغاز گرفت تا شروع گرفت کلی , از شروع گرفت کلی تا پایان گرفت کلی و از لحظه شروع باز شدن ماه تا پایان گرفت)می توان همزمان هم فاصله ماه تا زمین هم قطر ماه را بدست آورد.در بخش “خسوف “ به طور کامل این روش را توضیح و فرمول های آن را هم می آوریم .
اندازه گیری فاصله ماه تا زمین در هنگام کسوف بیشینه ای تاریخی دارد . نخستین بار آریستارخوس ( منجم و ریاضیدان یونان باستان ) در حوالی سال ۳۰۰ قبل از میلاد برای نخستین بار با استفاده از این روش توانست فاصله ماه تا زمین را حدود ۶۰ برابر شعاع زمین تعیین کرد .

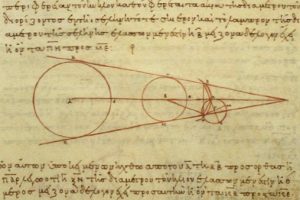
شکل شماره   ۱۰ – پاپیروس بدست آمده از آریستارخوس که محاسبات مربوط به فاصله ماه تا زمین در موقع کسوف در آن آمده است .

 ۵) محاسبه فاصله ماه تا زمین با استفاده از گرانش زمین

ماه در مدارش به دور زمین تابع قوانین گرانش می باشد . با استفاده از قوانین گرانش همانطور که با داشتن فاصله دوره تناوب ماهواره ها را اندازه می گیرند ( و برعکس با داشتن دوره تناوب فاصله ماهواره ها را اندازه می گیرند) با داشتن دوره تناوب ماه و جرم زمین می توان فاصله ماه تا زمین را محاسبه کرد .
در قسمت نیروهای کشندی بین ماه و زمین این روش را هم به طور مفصل توضیح می دهیم .

۶) اندازه گیری فاصله ماه تا زمین با تابش لیزر به ماه

سرنشینان آپولو ۱۱در تاریخ ۳۰ تیرماه ۱۳۴۸)وقتی به ماه سفر کردند دستگاه مسافت سنج لیزری را در سطح ماه قرار دادند (دو دستگاه دیگر هم سرنشینان آپولو ۱۴ و ۱۵ کار گذاشتند ) و دانشمندان از آن زمان به بعد به کمک این دستگاه ها توانستند در هر لحظه فاصله ماه تا زمین را با دقت کمتر از ۵ سانتیمتر بدست آورند .
مسافت سنج لیزری یک صفحه سیلیسی به قطر ۴۰ سانتیمتر است که روی پایه ای آلومینیومی به ابعاد حدود ۴۰ سانتیمتر مستقر شده است . و مانند هر آینه ای پرتوهای تابیده شده را در جهات مختلف بازتاب می دهد . روال کار به این صورت است که رصدخانه زمینی پرتوهای لیزر تک فاز ( تک رنگ ) را به سوی آینه مستقر شده در ماه می فرستند و زمان رفت و برگشت پرتو را با ساعت های بسیار دقیق اتمی اندازه گیری می کنند .
چون فاصله ماه تا زمین متغیر می باشد  بنابر این مدت زمان رفت و برگشت پرتو متغیر بوده ولی به طور متوسط چیزی حدود ۲/۵ ثانیه می باشد . که نصف ان که زمان رفت ( یا برگشت ) می باشد ۱/۲۵ ثانیه می باشد از آنجا که سرعت نور تقریبا ۰۰۰ر۳۰۰ کیلومتر در ثانیه می باشد بنابر این فاصله ماه تا زمین به طور متوسط :
کیلومتر ۰۰۰ر۳۷۵ = ۰۰۰ر۳۰۰ × ۱/۲۵
آنها برای ارسال پرتو از سامانه اپتیکی تلسکوپ استفاده می کنند . و این کار بر عکس موردی است که نور از چشمی تلسکوپ به چشم ما می رسد و ما می توانیم  ماه و اجرام سماوی را ببینیم . در این حالت بجای ورود نور از چشمی تلسکوپ باریکه لیزر وارد چشمی شده و به سمت هدف حرکت می کند و در نهایت پس از برخورد با هدف به دستگاه های اندازه گیری برخورد کرده تا زمان رفت و برگشت ثبت شود .
به نظر خیلی ساده می آید ولی با توجه با فاصله زیاد بین ماه تا زمین و حرکت و جابجائی ماه در آسمان و کوچکی باریکه لیزر در ابعاد ماه و زمین و… این کار بسیار طاقت فرسا می باشد .( مانند شلیک با یک کلت به سیبل “ هدف” در فاصله ۴۰۰ کیلومتری )
ابتدا باید ماه و محدوده آینه کار گذاشته شده را بدقت رصد کرده و پرتو لیزر را به سمت هدف روانه کنند ,پرتوی که به قطر مردمک چشم می باشد ولی وقتی به ماه برسد قطرش به بیش از۶مترمی رسد و در همه جهات متفرق می شود و در هنگام بازگشت شاید یک میلونیم قدرت پرتو اولی را نداشته باشد ولی دستگاه های اندازه گیری بقدری قوی است که حتی اگر یک فوتون هم باز گردد همان برای اندازه گیری زمان کافی است .

  

 شکل شماره ۱۱ – فرستادن پرتو لیزر به ماه و اندازه گیری زمان رفت و برگشت

 ۴- قطر ماه 

با دانستن فاصله ماه تا زمین اندازه گیری قطر ماه براحتی بدست می آید . برای محاسبه قطر ماه در نظر  می گیریم که قطر کره ماه قسمتی (کمانی ) از دایره عظیمه ای است که مرکز آن مرکز زمین و شعاع آن تا مرکز ماه می باشد . با داشتن فاصله ماه تا زمین(که حدود ۰۰۰ر۳۸۴ کیلومتر ) و اندازه زاویه ای قطر ماه (که حدودا ۳۱ دقیقه قوسی می باشد ) می توان براحتی قطر ماه را حساب کرد .
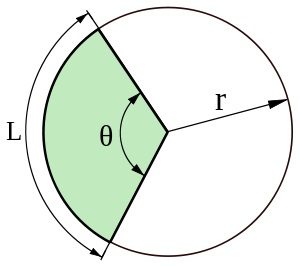
اندازه زاویه ای یک کمان را “اندازه کمان “ می نامند که از جنس زاویه بوده و بر حسب واحد های زاویه اندازه گرفته می شود . و مسافت بین دو انتهای کمان را “طول کمان “می نامند که از جنس طول بوده و بر حسب واحد های طول یا مسافت حساب می شود .
رابطه بین اندازه کمان و طول کمان عبارت است   L = θ× r که در آن θ اندازه کمان بر حسب رادیان و L طول کمان بر حسب واحد های طول و r شعاع دایره کمان می باشد .( شکل شماره ۱۲ )
حال در مورد در مورد ماه داریم :
۱) فاصله ماه تا زمین را r در نظر می گیریم این مقدار به طور متوسط ۰۰۰ر۳۸۵ کیلومتر است .
۲)  اندازه زاویه ای ماه را θ در نظر گرفته که این مقدار به طور متوسط ۳۱دقیقه قوسی می باشد که اگر به رادیان تبدیل کنیم ۰۰۹/ رادیان می شود .
۳) با این حساب قطر ماه  : حدود ۳۴۶۵ کیلومتر می شود  (  ۳۴۶۵  = ۰۰۹/ × ۳۸۵۰۰۰  )

برای مطالعه سایر مقاله های نجومی روی شکل زیر کلیک کنید.

برای مطالعه مقاله های روانشناسی اینجا  را کلیک کنید .

عکس های طبیعت, طبیعت خوانسار , شکوفه های بهاری  , گلستان کوه ,دانلود آلبوم های کامل بهترین و زیباترین عکس ها ,آلبوم هائی با صدها عکس کیفیت بالا ,  در هیچ کجای اینترنت این عکسها را پیدا نمیکنید , عکس هابدون استفاده از تکنیک های فتوشاپ تهیه شده , کاملا طبیعی 

برای آموزش کامل و حرفه ای گوگل مپ روی شکل زیر کلیک کنید

همه جیز در مورد گوگل مپ

۱) هر گونه اظهار نظر را در فرم اظهار نظر کاربران وارد کنید .
۲) نظرات بعد از تایید مدیریت نشان داده می شود .
۳) با انتقادات و پیشنهادات سازنده خود ما را هرچه بیشتر  همراهی کنید . مدیریت از انتقادات و پیشنهادات سازنده شما استقبال میکند .
۴) هرگونه بهره برداری : کپی تمام و یا قسمتی از مطالب این سایت بدون ارجاع منبع آن ممنوع می باشد .
۵) تکثیر فایل های Pdf با ذکر منبع آزاد ولی فروش آن تحت هر عنوان و با ذکر منبع هم ممنوع می باشد .