مکانیک مداری یا اخترپویاشناسی ( astrodynamics) شاخهای از علم مکانیک است که به حرکت اجرام آسمانی (کهکشان ها تا ستارگان و سیارات و قمرها و…) و مدارهائی که بر اثر گرانش متقابل یکدیگر تشکیل می دهند می پردازد . حرکت اجرام سماوی بر اساس قانون جاذبه عمومی نیوتن و همچنین قوانین کپلر(که بر گرفته از همان قانون گرانش جهانی است ) می باشد . مکانیک مداری علاوه بر توجیه مدارهای اجرام سماوی کاربرد گسترده ای هم در علم فضانوردی دارد.برای فرستادن فضاپیماها (با سرنشین و بدون سرنشین)به اعماق فضا همچنین در مدار قرار دادن ماهواره ها نیازمند این علم هستیم . در این مقاله در مورد مکانیک مداری و قوانین کپلرتوضیح می دهیم . و درمقاله “مکانیک مداری و قوانین کپلر(۲)“ ادامه این مقاله را می دهیم .
ولی قبل از آن توضیح کوتاهی راجع به گرانش و تاریخچه آن می دهیم .
۱- مختصری از گرانش
قبل از توضیح در موردحرکات مداری بهتر است در مورد گرانش و قانون جاذبه عمومی توضیحات مختصری بدهیم برای توضیحات کاملتر به لینک مقاله هائی که گذاشتیم (با رنگ آبی) مراجعه کنید .
بخصوص مقاله “ قانون جاذبه عمومی نیوتن“ را حتما مطالعه کنید .
۱) تاریخچه گرانش قبل از نیوتن
از دوران باستان برای بشر همواره سوال بود که چرا همه اشیا روی زمین سقوط می کنند ولی ماه و خورشید و ستارگان روی زمین سقوط نمی کنند؟ آنها تصور می کردند که زمین درمقایسه با ستارگان و ماه و خورشید بسیار وسیع و بزرگ است و ستارگان خیلی کوچک و نزدیک هستند که مانند یک سنگ و یا گلوله آتشین در روی زمین سقوط کنند آنها می پرسیدند که اگر زمین گرد و کروی می باشد چگونه در فضا معلق می باشد سقوط نمی کند( کچا سقوط کند ؟!! ) همچنین حرگت هماهنگ همه ستارگان از شرق به غرب برای آنها یک معما بود .
براین اساس بطلمیوس دانشمندیونانی (۹۰–۱۶۸ میلادی) نجوم بطلمیوسی را پایه گذاری کرد که بر اساس آن تمام ستارگان به کره ای به نام کره آسمان چسبیده اندو این کره (که مرکز آن زمین است)گرد زمین می چرخد همچنین ماه و خورشیدو سیارات هم روی کره های جداگانه قرارداشته و همگی گردزمین می چرخند۱۵۰۰سال طول کشیدتا کپرنیک منجم لهستانی (۱۴۷۳تا ۱۵۴۳)درکتابی به نام “گردش افلاک آسمانی “ توانست بطلان آن را نشان دهدو ثابت کندکه کره آسمان وجودنداشته و حرکات هماهنگ ستارگان نتیجه گردش زمین به دور خودش می باشد ستارگان هم از زمین بسیار دوربوده و گرد زمین نمی چرخند همچنین زمین و سیارات دیگر (۵سیاره شناخته شده)همگی گرد خورشید می چرخند.با وجود مخالفت سران کلیسا دانشمدان زیادی از جمله گالیله (گالیله سنگ بنای علوم تجربی را بر پایه آزمایش و تجربه نهاد) ازنظرات کپرنیک حمایت کردند.
دانش ستاره شناسی (همچنین سایر دانش ها) به مرحله بسیار حساس و مهمی رسیده بود و روز به روز بر دایره معلومات بشر افزوده می گشت.کپلر توانست سه قانون مهم حرکت سیارات را با توجه به رصدهای تیکوبراهه در آورده و همین مسئله راهی را در اختیار نیوتن گذاشت تا بتواند قانون گرانش عمومی را فرمول بندی کند . برای مطالعه کامل در این مورد به مقاله “تاریخچه گرانش “مراجعه کنید .
۲) زندگینامه نیوتن
سِر ایزاک نیوتن در ۲۵دسامبر۱۶۴۲ در روستای « وولستورپ » از توابع شهرلینکولنشیز انگلیس بدنیا آمد. نیوتن کودکی سختی داشت سه ماه قبل از بدنیا آمدنش یتیم شد و پدرش را از دست داد و مادرش در سه سالگی با یک کشیش ثروتمند ازدواج کرد و او را از خودش راند ولی این مانع از این نشد که مراحل ترقی را طی نکند بعلت هوش فوق العاده در ۱۸سالگی یعنی در سال ۱۶۶۱واردکالج ترینیتی (وابسته به دانشگاه کمبریج شد) و در سال ۱۶۶۵بعلت طاعون کالج تعطیل شذ و نیوتن در این مدت روی گرانش و فیزیک نور و..کارکرد (همچنین روی حساب دیفرانسیل و انتگرال و کیمیاگری و…) سرانجام در ۵ ژوئیه ۱۶۸۷نتیجه یافته های خود را در کتابی به نام “ اصول ریاضی فلسفه طبیعت “ با سرمایه ادموند هالی که او هم دانشمند و دوست نیوتن بود منتشر کرد و نام خود را جاودانه ساخت. برای توضیح کامل زندگینامه نیوتن به مقاله “ زندگینامه نیوتن“ مراجعه کنید.
۳) نیوتن چگونه قانون جاذبه عمومی را کشف کرد ؟
طبق یک داستان نیوتن روزی در باغ مادری خود درحال گردش بود که ناگهان سیبی ازدرخت افتاده و او را به فکر وا می دارد و پی به قانون گرانش جهانی می برد این داستان بسیار معروف است و حتی در محل خانه مادری نیوتن امروزه این درخت سیب موجود بوده و از آن حفاظت می شود و به یک جاذبه توریستی تبدیل شده است از طرف دیگر نیوتن با یادآوری یک بازی بچه گانه که در آن بچه ها سطل آبی را چرخانده و کسی که بتواند در حین چرخاندن سطل کمترین آب را از سطل بریزد برنده بازی می شود پی برد که نیروی گریز از مرکز با نیروی گرانش همدیگر را خنثی کرده و از این رو سیاره ها به درون خورشید سقوط نمی کنند . همچنین با اندازه گیری نیروی گریز از مرکزی که ماه را در مدارش به دور زمین نگه می دارد پی برد که نیروی جاذبه متناسب با عکس مجذور فاصله می باشد و سرانجام توانست فرمول نیروی گرانش جهانی را بدست اورده و نام خود را در تاریخ علم جاودانه کند . برای مطالعه کامل این که نیوتن چگونه توانست فرمول گرانش جهانی را بدست بیاورد به مقاله “ نیوتن و گرانش “ مراجعه کنید .
۴) قانون جاذبه عمومی نیوتن
قانون گرانش جهانی یا قانون جاذبه عمومی نیوتن به این شکل بیان می شود :
«بین هر دو جسم نیروی جاذبه ای وجود دارد که نسبت مستقیم با جرم آن دو جسم داشته و نسبت عکس با مجذور فاصله دارد »
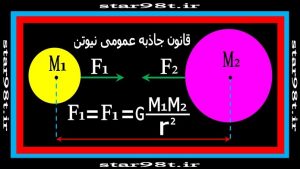
شکل شماره ۱ – قانون جاذبه عمومی نیوتن
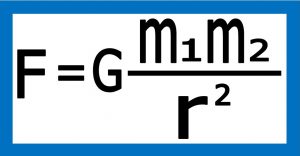
در این فرمول “G” ثابت گرانش نام دارد که ۶۰ سال بعد از مرگ نیوتن (در سال ۱۷۹۸)توسط هنری کاوندیش (دانشمند اهل ساردنی ) بدست آمد .
یکی از مهمترین مسائلی که نیوتن نشان داد و همیشه روی آن تاکید می کرد این بود که گرانش یک جسم کروی به گونه ای می باشد که انگار تمام جرم جسم در مرکز کره متمرکز شده است همچنین بر جسمی که داخل پوسته کروی قرار دارد هیچ نیروئی وارد نمی شود ( قضیه های پوسته )
برای مطالعه کامل در مورد گرانش به مقاله “قانون جاذبه عمومی نیوتن” مراجعه کنید .
۲- تاریخچه مکانیک مداری
کپلر و نیوتن و همینطور ادموند هالی پیشگامان مکانیک مداری بودند و توانستند راه را برای شناسائی مدارهای اجرام آسمانی باز کنند . بعد از این سه بزرگوار افراد دیگری نیز در این زمینه پیشگام شدند و توانستند دانش ما را درزمینه مکانیک سماوی گسترش دهند در این بخش در مورد مکانیک مداری و سیرتحول آن توضیح مختصری می دهیم توضیح بیشتر در این زمینه در بخش های دیگر این مقاله و مقاله های آینده داده می شود .
۱) مکانیک مداری در گذشته
در زمان های گذشته بشر هیچگونه درکی از حرکت اجرام آسمانی نداشت آنها از این که همه ستارگان و اجرام آسمانی به صورت هماهنگ از شرق به غرب در آسمان حرکت می کردند به این نتیجه رسیدند که ستارگان همچون نقاطی بر کره آسمان دوخته شدند و همراه کره آسمان به دور زمین می چرخند و بعد مسئله جابجائی تعدادی از ستارگان در زمینه ستارگان ثابت پیش آمد و بسیاری از اقوام از تعجب و وحشت حتی آنها را پرستش هم کردند ( پرستش میترا و آناهیتا و… ماه و خورشید و سایر سیارات ) سرانجام نظریه زمین مرکزی را بنیان نهادندتا بعد از ظهور کپرنیک و شروع رنسانس در اروپا به کمک ستارشناسان و دانشمندان دیگر( همچون گالیله و کپلر و نیوتن و…) حقایق اندک اندک روشن و مشخص شد .
۲) تیکو براهه و کپلر
تیکو براهه یکی از همین ستارشناسان و رصدگران بود او علاقه زیادی به ثبت رصد داشت و توانست موقعیت بسیاری از اجرام سماوی را با رصدهای مستقیم بدست آورده و در جداولی ثبت کند او جداول بسیار با ارزشی جمع آوری کرد که پس از مرگش در اختیار دستیارش کپلر قرار گرفت تا به وسیله آن سه قانون بسیار مهم خود را وضع کند . راجع به زندگینامه تیکو براهه و کپلر در بخش چهارم در مقاله “تاریخچه گرانش “توضیح کافی داده و همچنین در بخش پنجم تحت نام «۵- قوانین کپلر » توضیحات بیشتری داده می شود .
۳) نیوتن و قانون جاذبه عمومی
سرانجام نوبت نیوتن رسید . نیوتن با وضع قانون گرانش جهانی نه تنها مهر تاییدی بر قوانین کپلر زد بلکه توانست با استفاده از قانون گرانش جهانی و حساب دیفرانسیل و انتگرال این قوانین را ثابت کند . در مورد نیوتن و این که چگونه موفق به کشف قانون گرانش جهانی شد در مقاله های مختلف این فصل (فصل گرانش ) توضیح کافی داده شده است برای مطالعه به مقاله های “زندگینامه نیوتن “ و “ نیوتن و گرانش “مراجعه کنید .
۴) ادموند هالی
ادموند هالی در هشت نوامبر ۱۶۵۶در هاگرستون لندن در یک خانواده اشرافزاده و متمول چشم به جهان گشود. هالی در سال ۱۶۷۳به دانشگاه اکسفورد رفت ولی در سال ۱۶۷۶تحصیلات خود را تمام نکرد و برای ماجراجوئی به سنت هلنا رفت (در مورد زندگینامه هالی در مقاله های آینده توضیح خواهیم داد) هالی کشفیات زیادی در زمینه نجوم و مکانیک مداری انجام داده است . یکی از مهمترین کارهای هالی در این زمینه تعیین مدار دنباله دارها می باشد او اعتقاد داشت ستاره های دنباله دار نیز مانند سیارات مداری بیضی دارند و بنابراین برمی گردند . او بخصوص روی دنباله داری تمرکز کرد که امروزه به نام دنباله دار هالی شناخته می شود و هر ۷۵ سال یک بار برمی گردد . و بر اساس قوانین مکانیک مداری پیش بینی کرد که در سال ۱۷۵۷ باز می گردد (پیش بینی که به وقوع پیوست) همچنین هالی مشوق و ناشر کتاب “پرینکیپیا” نیوتن بود .
۵) اویلر و مکانیک مداری
لئونهارد اُویلر (Leonhard Euler) در ۱۵ آوریل ۱۷۰۷ در سوئیس بدنیا آمد او یکی از معروفترین و برجسته ترین ریاضیدانان جهان بود شهرت او بیشتر در روشی به نام روش اویلر در حل معادلات دیفرانسیل و انتگرال می باشد . وی همچنین در مکانیک، دینامیک سیالات، اپتیک و نجوم شهرت دارد.
در مورد زندگینامه اویلر در مقاله “ریاضیدانان بزرگ“ در آینده توضیح کامل خواهیم داد .
برای حل بسیاری از مسائل در ارتباط با مکانیک مداری و تعیین مدارهای بعضی از اجسام سماوی نیازمند حل معادلات دیفرانسیل و انتگرال بود و پیچیدگی بعصی مدارها کار را برای ستاره شناسان و ریاضیدانان مشکل می کرد . اویلر با روشی که به نام او روش اویلر شناخته می شود توانست بسیاری از این معادلات را حل کند . وی شخصا با استفاده از روشی که در حساب دیفرانسیل و انتگرال تعیین کرده بود توانست مدارهای دنباله دارها و سیارات و بسیاری از اجرام نجومی را تعیین کرده و به توسعه جداول نجومی کمک شایانی بکند .

شکل شماره ۲ – لئونهارد اُویلر
۶) قانون “بُد”
قانون “بُد” یا قانون تیفوس “بُد” یکی از مهمترین قانون ها در مکانیک مداری می باشد که امروزه اهمیت خود را از دست داده است این قانون توسط دو منجم به نام های“یوهان تیتیوس “و“یوهان بوده “وضع شدو در این قانون فرمولی ارائه شده که بر اساس آن فرمول فاصله سیاره های منظومه تا خورشید را می توانیم حساب کنیم.
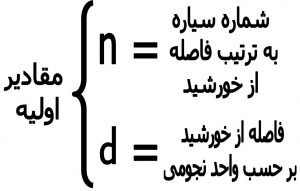
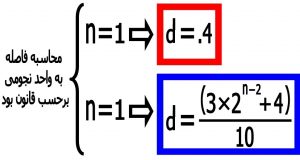
همانطور که دیده می شود طبق قانون بُد باید بین مدار مریخ و مشتری باید سیاره ای وجود داشته باشد از همین رو کوشش ها برای کشف سیاره جدید آغاز شدکه در قسمت بعدی در مورد آن توضیح می دهیم . همچنین در مقاله “ سیارات“ در مورد سیارات منظومه شمسی و چگونگی کشف آنها مفصل توضیح می دهیم .
جدول شماره ۱ – قانون بُد و فاصله سیارات از خورشید

۷) قانون “بُد” و کشف سیارات جدید
قانون بُد فاصله تعدادی از سیارات را از خورشید بدرستی نشان می داد (البته در مورد سیارات درونی مقدار دقیقی بود ولی هرچه جلوتر می رفت دقت آن کمتر می شد) ولی تعدادی از این سیاره ها در جدول وجود نداشتند ( بین مشتری و مریخ و همچنین بعد از زحل ) بنابراین تلاش برای کشف این سیارات آغاز شد . در سال ۱۷۸۱ ویلیام هرشل توانست اورانوس را در محل تعیین شده کشف کند .
بعد از کشف اورانوس ، در اول ژانویه ۱۸۰۱ منجمی سیسیلی به نام “جوزپه پیاتسی” موفق به کشف سیاره کوتوله سِرِس شد.(در مورد سیاره های کوتوله در مقاله “ پلوتون و سیاره های کوتوله “ توضیح کامل خواهیم داد) بعد از آن اجرام دیگری هم در همان نواحی کشف شدند که بعدها آن ناحیه به نام کمربند سیارکی نامیده شدند .
۸) کارل فریدریش گاوس Carl Friedrich Gauss
کارل فریدریش گاوس در تاریخ ۳۰آوریل ۱۷۷۷ از پدر و مادری فقیر در خانهای حقیر در شهر براونشوایگ در آلمان متولد شد . هوش و نبوغ او در همان کودکی آشکار شد و باعث حمایت دوک فردیناند برونسویک (یکی از اشراف آلمان)شد و با هزینه دوک در کالج کارولین و دانشگاه گوتینگن آلمان پذیرفته شد و بخاطر تحقیقات و کشفیات بزرگی که در ریاضیات داشت به او لقب «شاهزادهٔ ریاضیدانان» دادند بی شک گوس تاثیر گذارترین ریاضی دانان جهان می باشد .
کشفیات و کارهای گاوس را در زمینه مکانیک مداری در قسمت بعد شرح می دهیم . در مورد زندگینامه گاوس در مقاله“ریاضیدانان بزرگ“ در آینده توضیح کامل خواهیم داد .

شکل شماره ۳ – فریدریش گاوس
۹) گاوس و کشف مدار سرس
بعد از موقعی که “جوزپه پیاتسی” سیاره کوتوله سرس را کشف کرد سرس بیش از حد به خورشید نزدیک شده بود و امکان مشاهده دوباره آن امکان نداشت ولی تا یک سال دیگر قابل مشاهده بود ولی در پایان این مدت تعغیر مکان داده و امکان مشاهده دوباره آن بسیار مشکل بود و باید مکان دقیق آن روشن می شد . گاوس که در این زمان بیش از ۲۴ سال نداشت با استفاده از فرمول های ریاضی توانست روشی برای محاسبه مدار سرس پیدا کند و مسیر حرکت سرس را پیش بینی کند از این رو بعد از این که سرس به اندازه کافی از خورشید دور شد طبق پیش بینی های گاوس ستاره شناسان توانستند دوباره مکان سرس را در همان مکانی که گاوس پیش بینی کرده بود پیدا کنند .
۱۰) مکانیک مداری و شروع عصر فضا
با شروع سفرهای فضائی (عصر فضا ) اهمیت مکانیک مداری بیش از بیش آشکار شد از آن تاریخ به بعد مکانیک مداری به عنوان یک علم مستقل و زیر شاخه مکانیک شناخته شد.زیرا بعد از پرتاب فضاپیماها و کاوشگرها به فضا برای جلوگیری از مشکلات پرواز فضاپیماها ، مانورهای مداری ، تعغیر مسیر پرواز فضاپیماها و… نیازمند برنامه ریزی دقیق و پیش بینی مدار اجرام منظومه شمسی می باشد که خود بر اساس قوانین مکانیک مداری عمل می کند.درعصر فضا(نیمه دوم قرن بیستم)برای فرستادن فضاپیما ها به فضا روش ها و محاسبات بیشتری مورد نیاز بودو لازم بوده و هست تا ازفرمول های نسبیتی(در این مورد در مقاله “ گرانش و نسبیت عام “ توضیح دادیم) همچنین از روش های نوینی مانند کمک گرانشی ( در مقاله “ کمک گرانشی “ در این مورد توضیح دادیم ) هم استفاده کنند .
۳- مختصری از مقاطع مخروطی
یکی از مسائلی که “ قانون گرانش جهانی “ باید حل می کرد مسئله حرکت سیاره ها (گرد خورشید و یا ستاره مادر)و ستاره ها (ستاره های دوتائی و چند تائی و… همچنین حرکت هماهنگ ستاره ها حول مرکز کهکشان )و قمرها ( حول سیاره مادر ) و… اجرام نجومی بود .کپلر اولین بار اعلام کرد که مدار حرکت سیاره ها به دور خورشید بجای دایره بیضی می باشد . نیوتن نشان داد که مدار حرکت یک جسم به دور یک جسم دیگر نه تنها بیضی بلکه می تواند یکی از مقاطع مخروطی (دایره ، بیضی ، سهمی و هذولی ) باشد . بنابراین قبل از توضیح حرکات مداری (حرکت دو یا چند جسم حول مرکز جرم مشترک) توضیح کوتاهی در مورد مقاطع مخروطی می دهیم .
۱) هرم
اگر یک شکل دو بعدی بسته (مربع و مثلث و…تا اشکال غیر خاص مانند یک منحنی بسته)دریک صفحه داشته و همچنین نقطه ای درفضای سه بعدی خارج شکل درنظر بگیریم و از تمام نقاط شکل بسته به آن نقطه وصل کنیم یک شکل سه بعدی بدست می آید که هرم نامیده می شود.
برای مطالعه کامل در مورد هرم به مقاله “ هرم“ از همین سایت مراجعه کنید .

شکل شماره ۴ – هرم شش وجهی
۲) مخروط
مخروط در واقع نوعی هرم می باشد که قاعده آن به جای چند ضلعی دایره می باشد . همچنین می توان مخروط را از چرخش یک مثلث قائم الزاویه حول یکی از اضلاعش بدست آورد . مهمترین تفاوت هرم با مخروط در این است که قاعده هرم می تواند یک چند ضلعی(کوژ یا کاو) و یا یک منحنی بسته مانند دایره (بخاطر همین مخروط نوعی هرم است) یا بیضی یا هر منحنی دیگری باشد ولی قاعده مخروط فقط یک دایره کامل است .
برای مطالعه کامل در موردمخروط به مقاله “ مخروط “ از همین سایت مراجعه کنید .
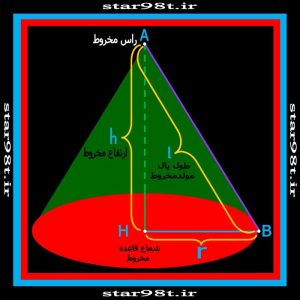
شکل شماره ۵ – قسمت های مختلف مخروط
۳) مخروط دوار
اگر دو خط متقاطع در یک صفحه داشته باشیم و یکی از خطوط دور خط دیگر شروع به دوران کند دو مخروط بی انتها بدست می آید که از طرف راس به هم چسبیده اند . خطی که دوران حول آن صورت گرفته خط محور مخروط و خطی که دوران کرده مولد مخروط نامیده می شود از آنجائی که این دو مخروط انتها ندارند حجم و قاعده و مساحت و مساحت جانبی نمی توان در مورد آن تعریف کرد . و این مهمترین تفاوت مخروط دوار با مخروط معمولی می باشد .
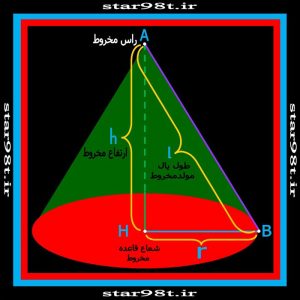
شکل شماره ۶ – مخروط دوار و قسمت های مختلف آن
۴) مقاطع مخروطی
در صورتی که یک مخروط دوار در فضا داشته باشیم و صفحه ای این مخروط را قطع کند بسته به این که چگونه و با چه زاویه ای مخروط را قطع کند شکل های مسطحی در صفحه پدید می آید که به آن مقاطع مخروطی می گویند. چهار شکل هندسی را به عنوان مقاطع مخروطی می شناسیم که عبارتند از : دایره ، بیضی ، سهمی و هذولی ( شکل های شماره ۷ و ۸ )
برای مطالعه در مورد مقاطع مخروطی به مقاله “ مقاطع مخروطی “ مراجعه کنید .

شکل شماره ۷ – کلیه مقاطع مخروطی
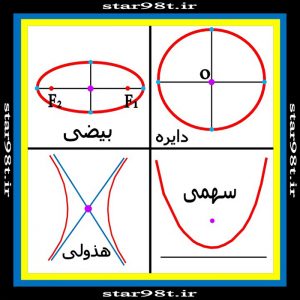
شکل شماره ۸ – مقاطع مخروطی دایره ، بیضی ، سهمی و هذولی
۵) معادله مقاطع مخروطی
مقاطع مخروطی اهمیت بسیار زیادی در تکنولوژی و علوم مختلف دارد برای همین به یکی از مهمترین مباحث هندسه تبدیل شده است .همچنان که در بخش های بعدی این مقاله توضیح می دهیم مسیر حرکت اجرام سماوی بر اثر گرانش و بسته به سرعت اولیه و نیروی گرانشی که وارد می شود یکی از مقاطع مخروطی می باشد . مقاطع مخروطی مانند هر شکل دیگری در صفحه مختصات ( دکارتی و یا قطبی و… ) دارای معادله ای هستند که این معادله را معادله مقاطع مخروطی می نامیم . معادله مقاطع مخروطی را به صورت معادله گسترده ، معادله کانونیک و یا معادله قطبی می نویسند .
برای مطالعه کامل در مورد انواع معادله مقاطع مخروطی و تبدیل آنها به یکدیگر به مقاله “ معادله مقاطع مخروطی “ از همین سایت مراجعه کنید .
۶) معادله قطبی مقاطع مخروطی
نیوتن برای اثبات قوانین کپلر از معادله قطبی مقاطع مخروطی استفاده کرد بنابراین در این مقاله قطبی مقاطع مخروطی را در نظر می گیریم . معادله قطبی مقاطع مخروطی از این قرار است .

شکل شماره ۹ – معادله قطبی انواع مقاطع مخروطی
۴- توپ نیوتن و مکانیک مداری
در بخش قبل در مورد مقاطع مخروطی توضیح دادیم (دایره ، بیضی ، هذولی و سهمی) زیرا مقاطع مخروطی در مکانیک مداری بسیار مهم می باشد به این دلیل که مسیر حرکت سیارات و قمرها و…سایر اجرام سماوی بر گرد یک جسم بسیار بزرگتر (پایه گرانش) یکی از مقاطع مخروطی است در این بخش فرض می کنیم توپی را به بالای کوه برده و به صورت افقی شلیک می کنیم می خواهیم بدانیم مسیرحرکت پرتابه به چه صورت است. لازم به ذکر است در تمام مسائلی که در این بخش در مورد مسیرحرکت پرتابه ها ذکر می کنیم از مقاومت هوا صرف نظر می کنیم .
۱) توپ نیوتن
نیوتن در کتاب اصول خود توپ بسیار بزرگ و پرقدرت را ذکر کرده که بالای یک کوه بلند برده و لوله آن را به صورت افقی(موازی با سطح زمین) گرفته و اقدام به شلیک می کنیم می خواهیم ببینیم مسیر گلوله
توپ با توجه به سرعتی که به گلوله می دهیم به چه صورت می باشد .
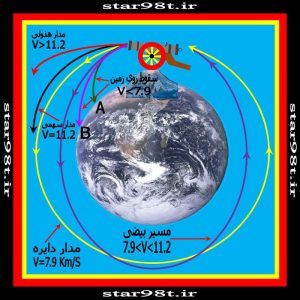
شکل شماره ۱۰ – توپ نیوتن در بالای کوه
۲) سقوط روی زمین
در صورتی که گلوله توپ سرعت کمی داشته باشد( کمتر از ۷/۹کیلومتر درثانیه) بعد از طی مسافتی به روی زمین سقوط می کند(در نقطه A )و اگر با سرعت بالاتری شلیک شود(بیشتر از سرعت قبلی ولی کمتر از ۷/۹کیلومتر در ثانیه ) مسافت بیشتری را روی زمین می پیماید ولی باز هم سقوط می کند(نقطه B)
۳) قرار گرفتن در مدار دایره ای
به همین ترتیب هر بار بار افزایش سرعت گلوله مسافت بیشتری را روی زمین می پیماید تا سرعت گلوله ۷/۹ کیلومتر در ثانیه برسد و در این صورت گلوله در مدار دایره ای در روی زمین قرار می گیرد . سرعت ۸ کیلومتر بر ثانیه حداقل سرعت مداری می باشد که گلوله را در مدار زمین نگه می دارد (در قسمت دهم همین بخش در مورد آن بیشتر توضیح می دهیم)به عبارت دیگر گلوله در روی زمین سقوط نمی کند ولی در مدار دایره ای بر گرد زمین میچرخد و برای همیشه در مدار زمین باقی می ماند. (شکل شماره ۱۰ مسیر دایره زرد )
۴) قرار گرفتن در مدار بیضی
اگر سرعت گلوله از۷/۹ کیلومتر در ثانیه بگذرد مدارگلوله به دور زمین به جای دایره بیضی می شود و هرچه سرعت از ۷/۹ کیلومتر در ثانیه بیشتر شود بیضی کشیده تر و هرچه به ۷/۹کیلومتر درثانیه نزدیکتر شود بیضی به دایره نزدیکتر می شود .(شکل شماره ۱۰مسیر بنفش)
۵) مدار سهمی و سرعت فرار
اگر سرعت گلوله به ۱۱/۲کیلومتر در ثانیه برسد گلوله توپ در یک مدار سهمی حرکت می کند . می دانیم که سهمی یک منحنی بسته نیست و اگر جسم ما در این مدار قرار بگیرد برای همیشه از حوزه جاذبه زمین فرار کرده و هیچگاه به زمین بر نمی گردد .(شکل ۱۰ مسیر سیاه رنگ )چنین سرعتی را “سرعت فرار” می نامیم
نکته : با مدارهای سهمی و هذولی پرتابه به زمین برنمی گردد ولی این مدار را سرعت فرار نمی نامند بلکه نام بهتر آن مدار فرار می باشد. (در مقاله “ سرعت فرار “ در مورد سرعت فرار توضیح کافی خواهیم داد )
۶) مدار هذولی
تا سرعت ۱۱/۲کیلومتر در ثانیه گلوله در مداری سهمی شکل از زمین دور می شود ولی اگر سرعت پرتاب گلوله ازسرعت فرار (۱۱/۲کیلومتر در ثانیه )هم بیشتر شود گلوله در مداری هذولی برای همیشه از زمین دور می شود و هیچگاه دیگر به زمین برنمی گردد .(شکل شماره ۱۰ مسیر قرمز )
۷) مدارهای باز و مدارهای بسته
مدارهای دایره و بیضی مدارهای بسته هستند بنابراین جسمی که در این مدارها میچرخددوباره به نقطه اول بر میگرددو برای همیشه (اگر هیچ نیروی خارجی تاثیر نکند)در مدارباقی می مانندولی مدارهای سهمی و هذولی مدارهای باز هستند و اگرجسمی در این مدارها قرار بگیرد دیگر هیچگاه به نقطه شروع حرکت برنمیگردد .
۷) خلاصه مطالب گفته شده
درجدول شماره یک خلاصه مطالب گفته شده در این بخش را می توانید ببینید .
جدول شماره ۲ – مسیر یک حرکت پرتابی در راستای افق با توجه به سرعت پرتاب گلوله (V)
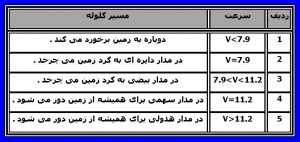
قبل از ادامه مطالب با توجه به جدول شماره یک لازم است به نکات زیر توجه کنید .
نکته یک : همانطور که در ابتدا گفته شد این مقادیر با این فرض می باشد که از مقاومت هوا صرف نظر کنیم اگر بجای بردن توپ در بالای کوه یک ماهواره را به ارتفاع مشخص ببریم و سرعت اولیه موازی سطح زمین به آن بدهیم همین نتیجه حاصل می شود . در ضمن در ارتفاعی که ماهواره ها در مدار قرار می گیردمقاومت هوا هم تقریبا وجود ندارد .
نکته ۲ : اعداد و مقادیر زیر برای زمین بوده اگر توپ نیوتن را بالای کوهی در یک کره دیگر ببریم با توجه به جرم سیاره و ارتفاعی که بالابرده می شود مقادیر متفاوتی حاصل می شود (در مورد سیارات مختلف این اعداد تفاوت می کند) که در بخش های بعدی به آن خواهیم پرداخت .
نکته ۳ : اثبات آنچه در جدول شماره یک آمده با توجه به فرمول دیفرانسیلی و برداری قانون گرانش جهانی انجام خواهد شد که در بخش ها و قسمت های بعدی به آن خواهیم پرداخت .
۸) مقاطع مخروطی و مدار پرتابه ها
مقاطع مخروطی شکل هائی هستند که از برخورد یک صفحه با مخروط دوار بدست می آیند ( بخش دوم « مختصری از مقاطع مخروطی» ) این شکل ها عبارتند از ( دایره ، بیضی ، هذولی و سهمی ) به علت این که مسیر حرکت سیارات و قمرها و… سایر اجرام سماوی بر گرد یک جسم بسیار بزرگتر ( پایه گرانش ) یکی از مقاطع مخروطی است مطالعه مقاطع مخروطی در نجوم بسیار مهم می باشد.(بخش دوم همین مقاله)
۹) سرعت مداری
سرعت مداری(Orbital speed) سرعتی است که یک جسم بسیار کوچک (در مقابل جسم بزرگ) باید داشته باشدتا بتواند بدون این که روی جسم بزرگ سقوط کندو یا ازحوزه گرانش جسم بزرگ فرار کندبه دور آن بچرخد. این جسم بزرگ می تواند خورشید باشد که سیاره ها دور آن می چرخند و یا سیارات (عطارد و ناهید و زمین و…) باشند که یک قمر طبیعی و یا مصنوعی (ماهواره ) به گرد آن بچرخد .
این سرعت مقدار ثابتی نیست و بستگی به مدار ماهواره (یا سیاره یا قمر طبیعی و..) دارد که دور جسم بزرگ دوران می کند که می تواند دایره یا بیضی باشدولی یک حداقل و یا حداکثری داردکه درمورد آن توضیح میدهیم.
۱۰) حداقل سرعت مداری
حداقل سرعت برای ماندن یک جسم کوچک در مدار جسم بزرگتر با توجه به فاصله جسم کوچکتر از مرکز جسم بزرگتر( یا ارتفاع از سطح جسم بزرگتر)، را «حداقل سرعت مداری » می نامند.با توجه به آنچه گفته شد این مدار باید دایره کامل باشد در غیر این صورت(سرعت بالاتر از حداقل) مدار به بیضی تغییر شکل خواهد دارد و هرچه سرعت بیشتر شود مدار بیضی کشیده تر می شود و اگر باز هم سرعت بیشتر شود مدار به سهمی و هذولی تغییر شکل خواهد داد و جسم کوچک از گرانش جسم بزرگ فرارخواهد کرد .
در حداقل سرعت مداری هرچه ارتفاع بیشتر باشد حداقل سرعت مداری کمتر خواهد شد(زیرا نیروی جاذبه سیاره کمتر میشود)بنابر این برای یک ماهواره که ارتفاع بیشتری دارد حداقل سرعت مداری کمتری هم دارد.
۱۱) سرعت مداری در سطح سیاره
فرض کنیم سطح زمین (یا هر سیاره مادر دیگر) عاری ازجو و هرگونه پستی و بلندی بود و ما یک ماهواره(یا قمر) را تقریبا درسطح زمین(ارتفاع صفر کیلومتر) قرار بدهیم. می خواهیم دوره تناوب و سرعت این ماهواره را بدست بیاوریم .در بخش چهارم مقاله “ مکانیک مداری و قوانین کپلر(۲) “(حرکت در سطح)در این باره بیشتر توضیح میدهیم و می بینیم که اگر دوره تناوب را بر حسب چگالی سیاره مادر بدست بیاوریم دوره تناوب به جرم و شعاع سیاره بستگی ندارد بلکه فقط به چگالی سیاره بستگی دارد این به آن معنی است که اگربه جای زمین هرسیاره دیگری باهمین چگالی زمین (۵/۵g/cm3) داشته باشیم همین سرعت بدست می آید . (شکل شماره ۱۱)
۱۲) سرعت لحظه ای و سرعت متوسط
گفتیم که هر چه ارتفاع قمر(یا ماهواره) بیشتر باشد سرعت مداری کمتر می شود بنابراین در مدارهای بیضی که قمر فاصله بیشتری از سیاره مادر پیدا می کند باید سرعت مداری کاهش یابد پس چرا سرعت دایره ای بیشترین سرعت در سرعت مداری می باشد ؟ این ظاهرا با آنچه گفتیم تناقض دارد .
در پاسخ باید گفت سرعتی که به آن اشاره کردیم سرعت لحظه ای می باشد برای قرار دادن یک جسم ( ماهواره) در مدار باید یک سرعت اولیه به ماهواره بدهیم اگر این سرعت اولیه حداقل باشد مدار دایره ای شکل می شود اگر بیشتر باشد مدار بیضی می شود . در مدارهای دایره ای شکل فاصله قمر از سیاره یکسان می باشد بنابر این سرعت ثابت بوده و سرعت متوسط و لحظه ای یکسان می باشد در مدارهای بیضی فاصله قمر از سیاره یکسان نبوده و در نقطه ای به حداقل(حضیض)و درنقطه ای به حداکثر(نقطه اوج) می رسد.بنابراین اگر چه با سرعت بیشتر ، مدار به جای دایره ای بیضی می شود ولی این سرعت ماکزیمم (سرعت درنقطه حضیض) میباشد و اگر سرعت متوسط را حساب کنیم می بینیم که سرعت متوسط در مدار بیضی کمتر از دایره می باشد و هر چه بیضی کشیده تر باشد سرعت متوسط هم کمتر می شود .
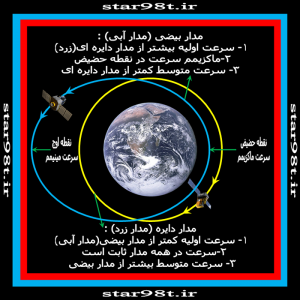
شکل شماره ۱۱ – تفاوت سرعت در مدار دایره ای و بیضی
۵- قوانین کپلر
یوهانس کپلر دانشمند بزرگ آلمانی قبل از کشف و فرمول بندی قانون گرانش عمومی بر مبنای یافته ها و رصدهای تیکوبراهه توانست برای حرکت سیارات بر گردخورشید سه قانون مهم وضع کند که به نام قوانین کپلر خوانده می شود . بعد از کشف قانون گرانش جهانی نیوتن بر اساس قانون گرانش جهانی توانست قوانین کپلر را ثابت کند در این بخش در مورد قوانین کپلر و نتایج آن توضیح می دهیم .
۱) کپلر و تیکوبراهه
یوهانس کپلر(Johannes Kepler)در۲۷دسامبر۱۵۷۱درشهر وایلدراشتات آلمان بدنیا آمد.او دانشمند، ریاضیدان و ستارهشناس مشهوری بود.کپلر در اصل می خواست کشیش شود ولی بخاطر هوش و نبوغش و با توصیه استادانش برای یادگیری ستاره شناسی عازم دانشگاه توبینگن آلمان شد و به تحصیل نجوم پرداخت .
از طرف دیگردرسال۱۵۴۶در کشور دانمارک منجم مشهوری پای به عرصه وجود نهاد که تیکوبراهه نام گرفت. تیکوبراهه (Tycho Brahe)دردانشگاه کپنهاگ و دانشگاههای آلمانی در رشته ستارهشناسی گذراند. و در سال ۱۵۷۶باحکم فردریک دوم (پادشاه دانمارک)مدیر رصدخانه سلطنتی دانمارک شد او تا سال۱۵۹۷(به مدت حدود ۲۰سال) که مدیر رصدخانه سلطنتی دانمارک بود دقیقترین رصدها و مشاهدات را ازحرکت سیارات ارائه داد و منبع ارزشمندی گردآوری کردکه تا آن زمان هنوز کسی ارائه نداده بود ( ازجمله آن که موقعیت و مختصات ۷۷۷ شی را بدقت ثبت کرد) در سال ۱۵۹۷بعلت درگذشت فردریک دوم و عدم حمایت جانشینش به آلمان آمدو منجم سلطنتی امپراتور آلمان (امپراتوری روم مقدس) شد .
تیکو براهه به محض این که در دربار امپراتوری روم مقدس به عنوان منجم سلطنتی انتخاب شد کپلر را به عنوان دستیار و معاون خود انتخاب کرد و از این به بعد بخت به کپلر روی آورد زیرا یک سال بعد تیکو براهه در گذشت(و یا به قولی توسط کپلر به قتل رسید) و کپلر با زیرکی جای او را گرفت و به گنجینه با ارزش
تیکوبراهه دست پیدا کرد و با توجه به آثار تیکوبراهه (که خود تیکو براهه نمی خواست منتشر شود )
توانست قوانین خود را نتیجه گیری کند .

شکل شماره ۱۲ – تیکو براهه و کپلر
۲) قوانین کپلر
کپلر با مطالعه و ادامه رصدهای تیکوبراهه توانست سه قانون خود را نتیجه گیری کند در اینجا ابتدا قوانین کپلر را آورده و در قسمت های بعد در مورد آنها توضیح بیشتری می دهیم .
۱-۲) قانون اول کپلر : مدارحرکت سیارات به گرد خورشید یک بیضی است که خورشید در یکی از دو کانون آن قرار دارد. (شکل شماره ۱۲)
۲-۲) قانون دوم کپلر : خط وصلکننده هر سیاره به خورشید در زمانهای مساوی مساحت های مساوی جاروب میکند.(شکل شماره ۱۲)
۳-۲) قانون سوم کپلر : نسبت مکعب فاصله متوسط هر سیاره تا خورشید به مربع زمان یک دور کامل گردش سیاره (دوره تناوب یا پریود ) تناسب مستقیم دارد.
نکته : در قانون سوم کپلر منظور از فاصله سیاره تا خورشید فاصله متوسط می باشد . که در مدارهای دایره ای شعاع دایره و در مدارهای بیضی نیم قطر بزرگ بیضی است .( مرکز خورشید کانون بیضی است )

شکل شماره ۱۳ – قانون اول و دوم کپلر
همچنین قانون دوم کپلر را در این تصویر متحرک می توانید مشاهده کنید :
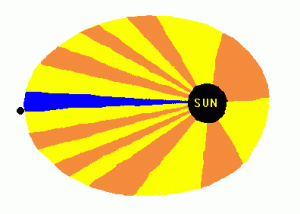
تصویر متحرک یک – قانون دوم کپلر
۳) مدل دایره ای مدار سیارات
بعد از آن که کپرنیک نظریه خورشید مرکزی را وضع کرد با توجه به اعتقادات آن روز مدار چرخش سیارات به دور خورشید را دایره کامل عنوان کرد . در آن زمان دایره شکل مقدسی بودکه از هر طرفی هماهنگی داشت و این موضوع از نظر آنها با نظم آفریننده همخوانی بیشتری از خود نشان میداد. از این رو بخاطر اعتقادات باطلی که تا آن زمان شکل گرفته بود منجمان که اعتقادات مذهبی هم داشتندغیر ازدایره کامل شکل دیگری نمی توانستند برای مدار سیارات تصور کنند .
۴) کپلر چگونه موفق به کشف قانون اول خود شد ؟
کپلر شروع به مطالعه و بررسی رصدهای تیکوبراهه و جداول نجومی او کرد . نجوم تیکوبراهه مخلوطی بود از مدل زمین مرکزی و خورشید مرکزی(نظریه تیکو براهه به این صورت بود که تمام سیارات دور خورشید می چرخند و خورشید دور زمین می چرخد) کپلر به مدل خورشید مرکزی کپرنیک اعتقاد کامل داشت و مدل تیکوبراهه را قبول نداشت ولی رصدهای او را بی نقص می دانست با این وجود متوجه شد رصدهای تیکو براهه به طور کامل در نظریه خورشید مرکزی صدق نمی کند بنابراین ۱۰سال از عمرخود را به تنهائی صرف بررسی حرکات سیارات کرد. ولی رصدها با واقعیت جور در نمی آمدبخصوص در مورد مریخ (تیکو براهه هم به این موضوع اشاره کرده بود) بنابراین کپلر مریخ را انتخاب کرد و روی آن به مطالعه و رصدپرداخت . او همه تلاش خود را کرد تا با توجه به مداردایره ای عدم تقارن ها را توجیه کند ولی نتوانست و موقعی که (بقول خودکپلر به او الهام شد) مدار را بجای دایره بیضی بگیرد همه چیز در جای خود قرار گرفت و عدم تقارن ها و ناهماهنگی ها از بین رفت از این رو کپلر طی قانون اول خود مدار سیاره ها را بجای دایره بیضی فرض کرد .
۵) ادامه تحقیقات کپلر و قانون دوم و سوم
کپلر در سال ۱۶۰۶ کتابی به نام “نجوم جدید” منتشر کرد که در آن قید شده بود همه سیارات در مداری بیضی شکل که خورشید در یکی ازکانون های آن قرار دارد به دور خورشید می چرخند و همچنین او تاکید کرد که هرچه سیاره به خورشید نزدیک تر باشد سرعت بیشتری هم دارد و بر این اساس قانون دوم خود را هم نتیجه گیری کرد که خط واصل بین خورشید و سیارات در زمان های مساوی مساحت های مساوی راجاروب می کند.
کپلر در سال ۱۶۱۸موفق به کشف قانون سوم خود هم شد .
قوانین کپلر دنیای نجوم را دگرگون کرد از این رو کپلر را پدر ستاره شناسی نوین می خوانند نکته قابل توجه این که قوانین کپلر قبل از کشف قانون جاذبه عمومی نیوتن وضع شده بود و همانطور که در قسمت بعد توضیح خواهیم داد از روی قانون جاذبه عمومی نیوتن قوانین کپلر را هم می توان اثبات کرد .
۶- اثبات قوانین کپلر
در بخش قبل در مورد قوانین کپلر و تاریخچه آن توضیح دادیم دیدیم که کپلر بر اساس رصدهای نجومی تیکو براهه توانست سه قانون در مورد حرکت سیارات وضع کند که به قوانین کپلر معروف شد ولی نتوانست آنها را اثبات کند . بعد از وضع قانون گرانش جهانی ، نیوتن درصدد برآمد قوانین کپلر را هم بر اساس قانون جاذبه عمومی اثبات کند در این بخش به اثبات قوانین سه گانه کپلر می پردازیم و در مقاله “ مکانیک مداری و قوانین کپلر (۲) ” به کاربرد قوانین کپلر و انواع مدارها می پردازیم .
۱) قوانین کپلر و منظومه های مداری
اگر چه کپلر قوانین سه گانه خود را فقط در مورد خورشید و سیارات وضع کرد ولی این قوانین اختصاص به سامانه خورشیدی ندارد و قابل تعمیم به هر سامانه مداری (منظومه های مداری) می باشد (مانند منظومه سیاره مشتری و قمرهایش و…) این قوانین از:حرکت سیاره ها به دور خورشید(و یا هر ستاره دیگری)،حرکت قمرها به دور سیاره ها،حرکت کره ماه و ماهواره ها به دور زمین …تا حرکت ستارگان به دور مرکز کهکشان و… همه جا قابل تعمیم است . در واقع قوانین کپلر یکی از نتایج بسیار مهم قانون جاذبه عمومی نیوتن می باشد .
از این رو در این بخش فرمول های مربوط به قوانین کپلر را ابتدا به صورت کلی(در مورد همه حرکت های مداری) آورده و بعدحرکت سیاره ها که حالت خاصی از قوانین کپلر می باشد را مورد بررسی قرار می دهیم . و البته قبل از آن در مورد نقطه اوج و حضیض توضیح می دهیم .
۲) نقطه حضیض و اوج و سرعت در نقطه اوج و حضیض
طبق قانون اول کپلر مدار سیاره ها به دور خورشید( و یا هر سامانه مداری دیگر ) بیضی می باشد بنابراین سیاره در نقاطی به خورشید دورتر و در نقاطی به خورشید نزدیکتر میشود. نزدیکترین فاصله سیاره تا خورشید را “نقطه حضیض” و دورترین فاصله تا خورشید را “نقطه اوج” مینامند. همچنین قانون دوم کپلر می گوید خط حاصل بین سیاره و خورشید در زمان های مساوی مساحت های مساوی جاروب میکند. لازمه این امر این است
که در نزدیکترین فاصله (نقطه حضیض) سرعت سیاره بیشتر و در نقطه اوج سرعت سیاره کمتر باشد .
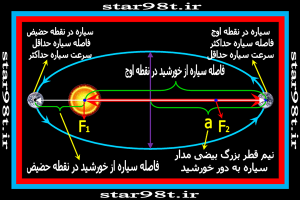
شکل شماره ۱۴ – تعریف اوج و حضیض
۳) اثبات قوانین کپلر
نیوتن بعد از کشف و فرمول بندی قوانین گرانش (که به صورت دیفرانسیلی و برداری نوشته شد ) اقدام به اثبات و حل بسیاری از مسائل مکانیک مربوط به گرانش از جمله قوانین کپلر کرد . به علت پیچیدگی و راه حل طولانی امکان نوشتن و توضیح جزئیات این اثبات ها در اینجا وجود ندارد . کسانی که آشنائی کامل با حساب دیفرانسیل و انتگرال و همچنین جبر برداری دارند می توانند اثبات قوانین کپلر در فایل زیر دانلود و مشاهده کنند .
فایل Pdf اثبات قوانین کپلر
[zarinpalpaiddownloads id=”22″]
۴) تعریف اصطلاحات به کار رفته
در این قسمت قانون سوم کپلر را در حالت کلی اثبات می کنیم(مربوط به همه منظومه های مداری ) و بعد در حالت خاص (حرکت سیارات به دور خورشید) تعمیم می دهیم . البته برای سادگی ابتدا مدارها را دایره کامل در نظر گرفته و بعد به بیضی تعمیم می دهیم .
بنابر این یک سامانه مداری در نظر گرفته و جرم مرکزی را «سیاره مادر» می نامیم باید توجه کرد که این سیاره مادر لزوما یک سیاره (به معنی نجومی آن)نیست بلکه جسم عظیمی است که اجسام کوچکتر دیگر( که فعلا ازگرانش اجسام کوچکتر نسبت به سیاره مادر صرف نظر می کنیم) درمدارهائی(دایره یا بیضی) به دور آن میگردند و منظور از قمر هم لزوما قمر به معنای نجومی آن(جسمی که دور یک سیاره می گردد )نیست. بنابر این سیاره مادر می تواند : خورشید و قمرها سیارات منظومه شمسی یا سیاره مادر کره زمین و قمرها ماهواره ها و یا سیاره مادر مرکز کهکشان و سیاره ها ستارگان و…باشند .
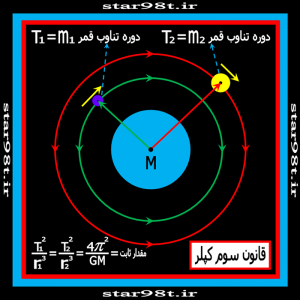
شکل شماره ۱۵ – قانون سوم کپلر
۵) اثبات قانون سوم کپلر
برای اثبات قانون سوم کپلر( شکل شماره ۱۵) بدین گونه عمل می کنیم
۱-۵) مقادیر اولیه : ابتدا مقادیر اولیه را می نویسیم .

۵-۲) نیروی گریز از مرکز و نیروی گرانش : نیروی جاذبه بین سیاره مادر و قمر را بر حسب قانون جاذبه عمومی نیوتن حساب کرده و مساوی نیروی گریز از مرکزی که قمر را در مدارش به دور سیاره مادر نگه می دارد قرار می دهیم :

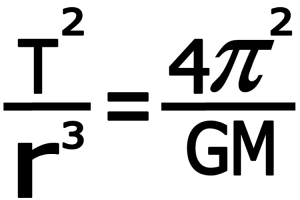
۳-۵) نتیجه نهائی : در نهایت می توانیم یکی از مهمترین معادلات مکانیک مداری را نتیجه گیری کنیم .
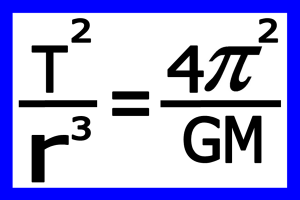
همچنان که دیده می شود این مقدار ثابت بوده و تنها به جرم سیاره مادر بستگی دارد .
توجه : به عنوان تمرین هم که شده با توجه به معادلات نوشته شده محاسبات مربوطه را انجام داده تا به نتیجه داده شده برسید . (ما در اینجا تنها نتیجه گرفته شده را نوشتیم )
نکته: اگر در مدارهای بیضی مقدار r را نیم قطر بزرگ بیضی بگیریم این فرمول درمدارهای بیضی هم درست است .
۶) اهمیت معادله قانون سوم کپلر
معادله فوق یکی از مهمترین و بنیادی ترین معادلات در مکانیک مداری می باشد به کمک این معادله تنها با داشتن دوره تناوب و فاصله یکی از قمرها می توان جرم سیاره مادر را حساب کرد . به کمک این معادله در منظومه شمسی با داشتن دوره تناوب زمین (که از هزاران سال قبل اندازه گیری شده بود) و فاصله زمین ازخورشید(در یک مقاله مجزا اندازه گیری فاصله زمین ازخورشید را توضیح می دهیم) و اندازه گیری دوره تناوب سیارات ( که بسیار آسانتر از اندازه گیری فاصله می باشد) می توان فاصله زمین از خورشید ، فاصله سیاره ها از خورشید و…بسیاری از مقادیر نجومی را محاسبه کرد ( در مقاله ” مکانیک مداری و قوانین کپلر (۲) ” در این باره بیشتر توضیح می دهیم .
۷) مدار سیارات منظومه شمسی
از نظر عملی مدار سیارات هر کدام از مقاطع مخروطی می تواند باشد ولی مدار هذولی و سهمی مدارهای باز هستند پس اگر در پیدایش منظومه شمسی (یا هر منظومه ستاره ای دیگر) اجسامی بودند که این مدارها را داشته اند دیگر جزء سامانه منظومه شمسی نیستند . پس می ماند مدارهای دایره و بیضی ، برای این که مدار دقیقا دایره ای باشد باید پارامترهای موجود (مانند سرعت اولیه و…) دقیقا مقدار مشخصی داشته باشد که امکان آن بسیار بعید است پس تنها بیضی می ماند حال این سوال پیش می آید که چرا مدارها بیضی نزدیک به دایره هستند (بخصوص سیارات درونی)در جواب باید گفت که در ابتدای پیدایش منظومه شمسی سیارات انرژی از دست می دادند و با از دست دادن انرژی سرعت آنها کاهش پیدا می کرد و مدارها به دایره ای نزدیکتر می شدند از این رو مدارها اگر چه بیضی هستند ولی به دایره بسیار نزدیک هستند. در این مورد در مقاله “ سیاره چیست؟ “ از فصل “ سیارات “ که در آینده منتشر می شود توضیح خواهیم داد .
۷- خلاصه مطلب
مکانیک مداری یا اخترپویاشناسی ( astrodynamics) شاخهای از علم مکانیک است که به حرکت اجرام آسمانی (کهکشان ها تا ستارگان و سیارات و قمرها و…) و مدارهائی که بر اثر گرانش متقابل یکدیگر تشکیل می دهند می پردازد . حرکت اجرام سماوی بر اساس قانون جاذبه عمومی نیوتن و همچنین قوانین کپلر(که بر گرفته از همان قانون گرانش جهانی است ) می باشد . مکانیک مداری علاوه بر توجیه مدارهای اجرام سماوی کاربرد گسترده ای هم در علم فضانوردی دارد.برای فرستادن فضاپیماها (با سرنشین و بدون سرنشین)به اعماق فضا همچنین در مدار قرار دادن ماهواره ها نیازمند این علم هستیم .
۱) تاریخچه مکانیک مداری
کپلر و نیوتن و همینطور ادموند هالی پیشگامان مکانیک مداری بودند و توانستند راه را برای شناسائی مدارهای اجرام آسمانی باز کنند . بعد از این سه بزرگوار افراد دیگری نیز در این زمینه پیشگام شدند و توانستند دانش ما را درزمینه مکانیک سماوی گسترش دهند با شروع سفرهای فضائی (عصر فضا ) اهمیت مکانیک مداری بیش از بیش آشکار شد از آن تاریخ به بعد مکانیک مداری به عنوان یک علم مستقل و زیر شاخه مکانیک شناخته شد.در این بخش در مورد مکانیک سماوی و سیرتحول آن توضیح مختصری می دهیم توضیح بیشتر در این زمینه در بخش های دیگر این مقاله و مقاله های آینده داده می شود .
۲) مختصری از مقاطع مخروطی
یکی از مسائلی که “ قانون گرانش جهانی “ باید حل می کرد مسئله حرکت سیاره ها ( گرد خورشید و یا ستاره مادر )و ستاره ها (ستاره های دوتائی و چند تائی و… همچنین حرکت هماهنگ ستاره ها حول مرکز کهکشان ) و قمرها (حول سیاره مادر ) و… اجرام نجومی بود .کپلر اولین بار اعلام کرد که مدار حرکت سیاره ها به دور خورشید بجای دایره بیضی می باشد . نیوتن نشان داد که مدار حرکت یک جسم به دور یک جسم دیگر نه تنها بیضی بلکه می تواند یکی از مقاطع مخروطی ()باشد . بنابراین نظر به اهمیت مقاطع مخروطی در مطالعه مکانیک مداری ، قبل از توضیح حرکات مداری (حرکت دو یا چند جسم حول مرکز جرم مشترک) توضیح کوتاهی در مورد مقاطع مخروطی می دهیم .
مقاطع محروطی اشکالی هستند که از برخورد یک صفحه با محروط دوار بوجود می آیندچهار شکل : دایره ، بیضی ، سهمی و هذولی مقاطع مخروطی نامیده می شوند در مقاله “ مقاطع مخروطی “ در مورد ان توضیخ می دهیم همچنین در مقاله “ معادله مقاطع مخروطی “ معادله این شکل ها را در دستگاه دکارتی و قطبی مورد بررسی قرار می دهیم . برای مطالعه به این دو مقاله رجوع کنید .
۳) توپ نیوتن و مکانیک مداری
در این بخش به مسیر و معادله پرتابه ای می پردازیم که از سطح زمین رو به بالا و یا از بالای یک کوه بلند به صورت افقی شلیک می شود می خواهیم بدانیم مسیرحرکت پرتابه به چه صورت است. لازم به ذکر است در تمام مسائلی که در این بخش در مورد مسیرحرکت پرتابه ها ذکر می کنیم از مقاومت هوا صرف نظر می کنیم .
در این بخش نشان می دهیم که جرکت گلوله توپ یکی از مقاطع مخروطی می باشد همچنین در این بخش در مورد سرعت مداری هم توضیح کوتاهی می دهم .
۴) قوانین کپلر و تاریخچه آن
یوهانس کپلر دانشمند بزرگ آلمانی قبل از کشف و فرمول بندی قانون گرانش عمومی بر مبنای یافته ها و رصدهای تیکوبراهه توانست برای حرکت سیارات بر گرد خورشید سه قانون مهم وضع کند که به نام قوانین کپلر خوانده می شود . بعد از کشف قانون گرانش جهانی، نیوتن بر اساس قانون گرانش جهانی توانست قوانین کپلر را ثابت کند در این بخش در مورد قوانین کپلر و تاریخچه آن توضیح می دهیم این که کپلر چگونه به این قوانین دست یافت و این که قوانین کپلر چقدر اهمیت دارد و… در بخش بعد آن را اثبات می کنیم .
۵) اثبات قوانین کپلر
در بخش قبل در مورد قوانین کپلر و تاریخچه آن توضیح دادیم دیدیم که کپلر بر اساس رصدهای نجومی تیکو براهه توانست سه قانون در مورد حرکت سیارات وضع کند که به قوانین کپلر معروف شد ولی نتوانست آنها را اثبات کند . بعد از وضع قانون گرانش جهانی ، نیوتن درصدد برآمد قوانین کپلر را هم بر اساس قانون جاذبه عمومی اثبات کند در این بخش به اثبات قوانین سه گانه کپلر می پردازیم و در مقاله “ مکانیک مداری و قوانین کپلر (۲)” به کاربرد قوانین کپلر و انواع مدارها می پردازیم .
نظر به این که اثبات قوانین اول و دوم کپلر پیچیده بوده یک فایل ضمیمه برای اثبات آن قرار می دهیم .
![]()
برای مطالعه سایر مقاله های نجومی روی شکل زیر کلیک کنید.
![]()
برای مطالعه مقاله های روانشناسی اینجا را کلیک کنید .
![]()
عکس های طبیعت, طبیعت خوانسار , شکوفه های بهاری , گلستان کوه ,دانلود آلبوم های کامل بهترین و زیباترین عکس ها ,آلبوم هائی با صدها عکس کیفیت بالا , در هیچ کجای اینترنت این عکسها را پیدا نمیکنید , عکس هابدون استفاده از تکنیک های فتوشاپ تهیه شده , کاملا طبیعی
![]()
برای آموزش کامل و حرفه ای گوگل مپ روی شکل زیر کلیک کنید
![]()
۱) هر گونه اظهار نظر را در فرم اظهار نظر کاربران وارد کنید .
۲) نظرات بعد از تایید مدیریت نشان داده می شود .
۳) با انتقادات و پیشنهادات سازنده خود ما را هرچه بیشتر همراهی کنید . مدیریت از انتقادات و پیشنهادات سازنده شما استقبال میکند .
۴) نوشته های قرمز پر رنگ ارجاع به لینک هستند که هنوز لینک آنها قرار داده نشده است ( هنوز صفحه آنها منتشر نشده است )
۵) نوشته های آبی پر رنگ ارجاع به لینک هستند که لینک آنها قرار داده شده است ( صفحه آنها منتشر شده است )
۶) هرگونه بهره برداری : کپی تمام و یا قسمتی از مطالب این سایت بدون ارجاع منبع آن ممنوع می باشد .
۷) تکثیر فایل های Pdf با ذکر منبع آزاد ولی فروش آن تحت هر عنوان و با ذکر منبع هم ممنوع می باشد.
![]()