مقاطع مخروطی اهمیت بسیار زیادی در تکنولوژی و علوم مختلف دارد برای همین به یکی از مهمترین مباحث هندسه تبدیل شده است . در مقاله “مقاطع مخروطی “ تعریف مقاطع مخروطی و ویژگی های آنها را توضیح دادیم . همچنین مقاله های “مخروط ” و “ هرم“و مقاله “دستگاه های مختصات در ریاضی” را هم حتما مطالعه کنید . (فایل Pdf همراه این مقاله موجود می باشد که آن را هم دانلود کرده و مطالعه کنید)
در این مقاله مقاطع مخروطی را از دیدگاه تحلیلی مورد بررسی قرار می دهیم . معادله جبری آنها را بدست آورده و در صفحه مختصات آنها را رسم می کنیم .
۱- خلاصه ای از مباحث مطرح شده در این مقاله
در این بخش خلاصه ای از آنچه در بخش ها و قسمت های مختلف این مقاله شرح داده می شود توضیح داده شده است . توضیحات ایتدا از عبارات جبری و بعد سیستم مختصات دکارتی شروع می شود فقط به قصد یادآوری ( چون برای مراحل بعد مهم است ) و بعد معادلات ضمنی و کانونیک در بخش های بعد تشریح میشود.
۱) اهمیت معادلات مقاطع مخروطی
همانطور که گفته شد معادلات مقاطع مخروطی در بسیاری از علوم (نجوم و…) کاربرد دارد.برای مثال برای محاسبه مسیرحرکت اجرام آسمانی به مقاطع مخروطی نیاز داریم . نیروهای مختلفی به اجرام آسمانی وارد می شود که ناشی از تاثیر گرانش است بر حسب سرعت و جهت ، این نیروها مسیرهای مختلفی به اجرام آسمانی می دهند دانشمندان در صفحه ای که این اجرام حرکت می کنند معادله مسیر حرکت را نوشته و ثابت می کنند این معادله یکی از مقاطع مخروطی می باشد . بنابراین درک مکانیک سماوی (حرکت اجرام آسمانی) بدون شناخت معادلات مقاطع مخروطی امکان پذیر نمی باشد بنابراین در این بخش در مورد معادلات مقاطع مخروطی بحث کرده و آنها را توضیح می دهیم . ولی بخاطر جلوگیری از طولانی شدن مطلب از آوردن مثال های عددی خودداری کرده و معادلات را فقط برحسب پارامترها حل کرده تا به نتیجه برسیم .
۲) عبارات جبری
چون مطالب این مقاله در رابطه با محاسبات جبری می باشد توضیح بسیار کوتاهی راجع به عبارات جبری و چند جمله ای ها و محاسبات جبری می دهیم . مطالب توضیح داده شده کافی نیست و خواننده برای درک و فهم مطالب این بخش باید تا حدودی اطلاعات کافی در مورد محاسبات جبری حداقل در سطح تحصیلات متوسطه (رشته های ریاضی و تجربی) داشته باشد. با این وجود چون برای درک و فهم مطالب مربوط به محاسبه معادلات مقاطع مخروطی نیاز به محاسبات جبری می باشد این بخش گنجانده شده است.
۳) سیستم مختصات دکارتی و پاره ای از مسائل مربوط به آن
هدف از این فصل بررسی و بدست آوردن معادله مقاطع مخروط می باشد و چون فهم این معادلات بدون دانستن مختصات دکارتی و تعریف مختصات نقطه و خط و رسم منحنی ها در سیستم مختصات دکارتی امکان پذیر نیست در این بخش توضیحات کوتاهی راجع به محورهای مختصات و معادله خط و فاصله دو نقطه و فاصله نقطه از خط و… همچنین انتقال محورهای مختصات داده و فرمول های آن را بیان می کنیم مطالب این بخش در کلیه مطالب گفته شده در بخش های بعدی که مربوط به بدست آوردن معادله مقاطع مخروطی می باشد کاربرد داشته و هدف از اضافه کردن این بخش به مقاله هم همین بوده است .
۴) معادلات گسترده یا ضمنی مقاطع مخروطی
مقاطع مخروطی (دایره ،بیضی ، سهمی و هذولی) همانند هر شکل دیگری در سیستم های مختلف مختصات، معادله جبری مربوط به خودشان را دارند به گونه ای که با رسم این معادلات در سیستم های مختلف می توان آن شکل را بدست آورد . در اینجا معادلات گسترده یا ضمنی مقاطع مخروطی را توضیح می دهیم .
در ابتدا شکل کلی معادلات درجه دوم نسبت به x وy را نوشته و بدون این که اثبات کنیم فرمول حالت هائی که معادلات درجه دوم به یکی از مقاطع مخروطی تبدیل می شود را می نویسیم و در نهایت در جدولی همه آنها را جمع بندی می کنیم .
نکته بسیار مهم این است که معادلات ذکر شده در مورد مقاطع مخروطی قائم (در راستای محور y ها ) و یا افقی ( در راستای محور xها ) ذکر شده است و نه مقاطع مخروطی مایل , مقاطع مخروطی مایل مقاطعی هستند که محور یا قطر آنها نه با محور x ها و نه با محور y ها موازی باشد که بعلت پیچیدگی های آن خارج از بحث این مقاله می باشد ولی می توان ثابت کرد که اگر مقاطع مخروطی مایل را هم در نظر بگیریم هر معادله درجه دوم بر حسب x وy ( یعنی حالت کلی Ax2+Bxy+Cy2+Dx+Ey+F=0 ) حتما یکی از مقاطع مخروطی می باشد .
۵)معادلات کانونیک مقاطع مخروطی
در سیستم مختصات دکارتی هر مقطع مخروطی معادله مربوط به خودش را دارد که در بخش چهارم شرح داده و خلاصه آن را در جدول شماره دو آوردیم . ولی جدول فوق مشخصات و جزئیات مقاطع مخروطی ( مرکز و کانون و خط هادی و…راس ) را مشخص نمی کنداز این رو به معادلاتی نیاز داریم تا مشخصات وجزئیات مقاطع مخروطی را مشخص کند . این معادلات را معادله کانونیک مقاطع مخروطی می نامیم .
در این بخش هم معادلات کانونیک مقاطع مخروطی را بدون اثبات آورده و بعد درجدولی جمع بندی می کنیم.
۶)معادلات کانونیک دایره و بیضی و سهمی و هذولی
در بخش های ۶ تا ۹ از روی تعریف مقاطع مخروطی (دایره ، بیضی ، سهمی و هذولی) معادله کانونیک آنها را ابتدا برای حالتی که مرکز و یا راس آنها در مبدا مختصات باشد بدست آورده و بعد با استفاده از فرمول انتقال مبدا مختصات معادله آنها را برای حالت کلی بدست می آوریم . ( مطالب گفته شده در بخش پنجم را ثابت می کنیم ) و بعد با محاسبات ثابت می کنیم که این معادلات قابل تبدیل شدن به معادله گسترده نیز می باشد همچنین روش هائی را نشان می دهیم که بتوان از روی معادله گسترده به معادله کانونیک مقاطع مخروطی رسید .
بنابراین در هر بخش و در مورد هر مقطع مخروطی به ترتیب این عملیات را انجام می دهیم .
۱- بدست آوردن معادله کانونیک از روی تعریف مقاطع مخروطی
۲- تبدیل معادله کانونیک به گسترده و برعکس
۷) معادلات قطبی مقاطع مخروطی
تا اینجای کار هرچه گفته شد (معادلات کانونیک و گسترده )در صفحه مختصات دکارتی بود ولی در بسیاری از مسائل فیزیکدان ها ترجیح می دهند که بجای مختصات دکارتی از مختصات قطبی استفاده کنند . مسیر اجرام سماوی را هم به صورت معادلات در مختصات قطبی می نویسند بنابراین لازم است توضیح کوتاهی نیز راجع به معادله قطبی مقاطع مخروطی داده شود که در بخش دهم(که آخرین بخش این مقاله می باشد)به طورخیلی خلاصه با معادلات قطبی مقاطع مخروطی ( البته بدون اثبات ) آشنا می شویم .
۲- عبارات جبری
بسیاری از مفاهیم اولیه فیزیک به صورت فرمول های ریاضی بیان می شود این فرمول ها را به معادلات جبری تبدیل کرده و با بررسی و حل آنها بسیاری از مفاهیم فیزیکی را توضیح می دهند . در این مورد در مقاله ای جداگانه کلیه این مبحث را شرح می دهیم در اینجا فقط توضیح کوتاهی در مورد عبارت های جبری می دهیم.
۱) عبارت جبری
به صورت خیلی ساده و مختصر یک عبارت جبری مجموعه ای از اعداد و حروف می باشد ( که حروف نماینده اعداد می باشند ) و با چهار عمل اصلی و توان و رادیکال و … به هم مرتبط شده اند در صورتی که هیچگونه علامت تساوی “=” وجود نداشته باشد صرفا عبارت جبری نامیده می شود و در صورت وجود یک علامت تساوی یک معادله جبری نامیده می شود . به عبارت دیگر یک معادله جبری مجموع دو عبارت جبری می باشد که بین آنها علامت تساوی وجود دارد .
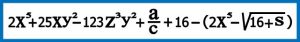
یک عبارت جبری
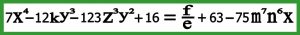
یک معادله جبری
۲) جمله در عبارات جبری
هر جمله در عبارات جبری مجموعه ای از حروف و اعداد می باشد که بین آنها فقط ضرب و تقسیم وجود داشته باشد و جمع و تفریق نباید وجود داشته باشد .
۲-۱) یک جمله ای : عبارت جبری می باشد که فقط از یک جمله تشکیل شده باشد .
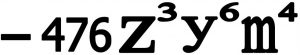
یک جمله ای
۲-۲) چند جمله ای : عبارت جبری می باشد که از چند جمله تشکیل شده باشد .
![]()
سه جمله ای
۳) درجه در عبارات جبری
حروف در عبارات جبری توان های مختلفی دارند توان هر حرف در یک عبارت جبری درجه آن عبارت نسبت به آن حرف می باشد که در اینجا این موضوع را بیشتر بررسی می کنیم .
۳-۱)درجه یک جمله ای نسبت به یک حرف : توان آن حرف در یک جمله ای را درجه یک جمله ای نسبت به آن حرف می گویند مثلا در یک جمله ای” “ ۳x3y5z4 درجه نسبت به “y” پنج و نسبت به “z” چهار می باشد .
۳-۲)درجه یک جمله ای نسبت به تمام حروف :درجه یک جمله ای نسبت به تمام حروف مجموع توان های تک تک حروف می باشد مثلا در یک جمله ای “ ۳x3y5z4 ” درجه نسبت به تمام حروف ۱۲=۴+۵+۳ میباشد.
۳-۳)درجه چندجمله ای نسبت به یک حرف : درجه چندجمله ای نسبت به یک حرف درجه جمله ای است که بزرگترین درجه را داشته باشد . مثلا درجه چند جمله ای “ ۴x5y3z2+7x2y7-4x4y5z ” نسبت به x پنج است .
۳-۴)درجه چندجمله ای نسبت به تمام حرف : درجه جمله ای است که بزرگترین درجه را نسبت به تمام حروف داشته باشد . مثلا درجه چند جمله ای“ ۴x5y3z4+7x2y7-4x4y5z ” نسبت به تمام حروف دوازده است .
۴) جملات متشابه در چند جمله ای ها و ساده کردن چند جمله ای
در یک چند جمله ای جملاتی وجود دارند که قسمت حرفی (قسمتی که فقط از حروف تشکیل شده است ) آنها مانند هم است این جملات را جملات متشابه می نامند و قابل جمع و تفریق هستند . برای انجام عملیات روی عبارات و معادلات جبری باید از روش های مختلفی (مانند اتحادها و… که در مقاله های آینده شرح می دهیم) آنها را به گونه ای ساده کنیم که هیچ جمله متشابهی وجود نداشته باشد .
۳- سیستم مختصات دکارتی و پاره ای از مسائل مربوط به آن
سیستم های مختصات در ریاضی و فیزیک و … نجوم و…علوم مختلف کاربرد های گسترده ای دارد فرمول های فیزیکی را به صورت معادلات جبری در آورده و با حل آنها بسیاری از پدیده ها را توضیح می دهند و … همچنین آنها را به صورت نمودار در آورده و روی نمودارها و شکل های حاصل از نمودارها بسیاری از پدیده ها را توجیه می کنند بنابراین رسم نمودار ها و هندسه دکارتی اهمیت بسیاری در ریاضی و فیزیک و… علوم مختلف دارد .
در مورد هندسه دکارتی در یک مقاله مجزا به نام “ هندسه دکارتی “ توضیح کامل می دهیم . آنچه در اینجا ذکر می شود خلاصه ای از هندسه دکارتی در ارتباط با مقاطع مخروطی و رسم منحنی آنان است .
۱) سیستم های مختصات دکارتی
درفضای بیکران و یا روی یک صفحه مسطح ویا یک کره و یا حتی یک خط راست برای این که بتوان موقعیت یک مکان ( نقطه , شی و… )را تعیین کرد باید از سیستم مختصات استفاده کرد در همه سیستم های مختصات از یک نقطه به نام مبدا استفاده می شود و نقاط دیگر ( روی خط یا صفحه یا فضا) به وسیله روابطی (که درهر سیستم مختصات با دیگری متفاوت است) به نقطه مبدا مرتبط می باشند .
یکی از این سیستم ها سیستم مختصات دکارتی می باشد. برای آشنائی با سیستم مختصات دکارتی به مقاله “ مختصات در ریاضیات “ مراجعه و یا اصل مقاله را از “ اینجا “ دانلود کنید .
۲) معادله یک شکل در فضای دو بعدی و سه بعدی
هر شکلی (خط راست ، دایره ، بیضی و…) از تعداد نامتناهی نقطه تشکیل شده است . در دستگاه مختصات دکارتی (دو بعدی) هر نقطه با دو مختصات(x,y) تعریف می شود . در بسیاری از شکل ها یک یا چند رابطه جبری (معادله جبری ) بین x,y برقرار می باشد . به گونه ای که مختصات تمام نقاط واقع بر آن شکل درآن معادله یا معادلات صدق می کند. این معادلات جبری را معادله آن شکل دردستگاه محتصات دکارتی می نامند.
شکل های منظم هندسی برای خودشان معادله دارند مثلا معادله خط راست عبارت است از y=ax+b که در آن aوb مقادیر معلوم و y,x مختصات نقاط روی خط هستند . حال اگر بجای خط راست نیم خط باشد کافی است شرطی گذاشته شود و مقدار xوy را محدود کنیم و اگر منظور یک چهار ضلعی مانند مستطیل یا لوزی و… باشد بجای معادله یک پاره خط ، چهار معادله و برای چهار پاره خط می نویسیم و… و این چهار رابطه چهار نیم خط را می سازد که در نهایت یک چهار ضلعی را تشکیل می دهد و…
در فضای سه بعدی معادله جبری که تشکیل می دهیم بجای دو مختصات (yوx) با سه مختصات (zوyوx) آنها را بهم مربوط می کنیم و در دستگاه مختصات سه بعدی آنها را رسم می کنیم .
در سیستم مختصات دیگر ( مانند مختصات قطبی و استوانه ای و… ) برای مختصات نقاط به جای (yوx) و یا (zوyوx) از حروف دیگری استفاده می شود که مختصات نقاط در آن سیستم ها می باشند ( مثلا در مختصات قطبی از” θ و r “ استفاده می شود )
۳) پارامتر چیست ؟
در معادله ای مانند y=ax+b اگر چه درنگاه اول چهار مجهول داریم( a و b و x و y ) ولی چون x و ٰy مختصات نقاط مختلف می باشند از این رو ” b و a ” را به جای مجهول “پارامتر “ می نامند و در واقع معادله ای مانند y=ax+b تنها معادله یک خط مشخص نیست بلکه معادله تعداد نامحدودی خط است که با تعغیر پارامترهای ” b و a “ خطوط مختلفی بدست می آید .
۴) فاصله دو نقطه در سیستم مختصات دکارتی
اگر در سیستم مختصات دکارتی نقطه A(xa,ya) و b(xb,yb) را داشته باشیم فاصله دو نقطه A و B را بدین ترتیب بدست می آوریم .
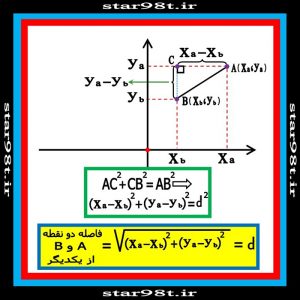
شکل شماره ۱ – بدست آوردن فاصله بین دو نقطه در صفحه مختصات دو بعدی
بنابراین با توجه به شکل فاصله بین دو نقطه عبارت می شود از :

همچنین با عمومیت دادن به مختصات سه بعدی فضائی فاصله دو نقطه درفضای سه بعدی به این ترتیب است:

۵) معادله خط راست
معادلاتی که بر حسب x و y از درجه اول باشند معادله خط راست نامیده می شوند بنابر این صورت کلی معادله خط راست عبارت است : Ax+by+c=0 می باشد که برای تعیین خصوصیات خط طرفین معادله را به A تقسیم کرده و به این صورت هم می نویسند : y=ax+b که در این صورت پارامتر “a” را ضریب زاویه و پارامتر “b” را به عنوان عرض از مبدا می نامند . ( شکل شماره ۲)
توضیح کامل این مطلب در مقاله “ هندسه دکارتی “ بزودی منتشر می شود .
۶) خطوط موازی محورها
خطوطی که موازی محورها می باشند معادله آنها به این صورت نوشته می شوند .
۱-۶) خطوط موازی محور x ها ( محور طول ها ) : معادله این خطوط به صورت y=b نوشته می شود .
۲-۶) خطوط موازی محور y ها ( محور عرض ها ) : معادله این خطوط به صورت x=a نوشته می شود .
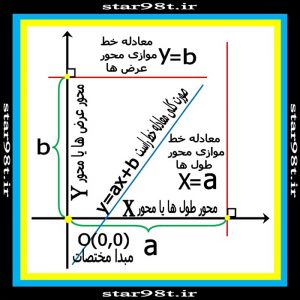
شکل شماره ۲ – انواع معادله خط راست
۷) فاصله نقطه از خط
فاصله نقطه از خط در واقع کوتاه ترین مسیری است که نقطه را به خط وصل می کند. برای پیدا کردن فاصله یک نقطه تا یک خط معادله خط را نوشته و بعد با استفاده از شکل و همچنین روش های مختلف در “ هندسه دکارتی “ فاصله نقطه از خط را بدست می آوریم در این قسمت فقط فرمول ها را آورده و اثبات فرمول ها در مقاله “ هندسه دکارتی “ می آوریم .



۸) انتقال محورهای مختصات
گاهی اوقات لازم است محورهای مختصات را به نقطه دیگر انتقال بدهیم این حالت وقتی بروز می کند که مثلا برای بدست آوردن معادله یک شکل مجبوریم ابتدا آن را در مبدا مختصات در نظر بگیریم و بعد برای بدست آوردن معادله حالت های کلی آن شکل ( جائی غیر از مبدا مختصات) مبدا مختصات را عوض می کنیم . و با استفاده از فرمول های تبدیل مبدا جدید به قدیم معادله کلی آن را می نویسیم .
در بخش های بعد خواهیم دید که چگونه برای بدست آوردن معادله مقاطع مخروطی ابتدا حالت خاص آنها را در نظر گرفته که مرکز و یا راس(دایره و بیضی و هذولی مرکز و سهمی راس سهمی ) آنها در مبدا مختصات باشد و بعد یک مبدا جدید رسم کرده به گونه ای که راس و مرکز مقاطع مخروطی به جای مبدا دستگاه قدیم روی مبدا دستگاه جدید قرار بگیرد و معادله را برای دستگاه جدید نوشته و از طریق تبدیل مختصات دستگاه جدید به مختصات دستگاه قدیم معادله برای نقطه ای غیر از مبدا مختصات نوشته می شود .
رابطه بین مختصات دستگاه قدیم و جدید به این صورت است (با توجه به شکل شماره ۳ براحتی می توانید به این روابط پی ببرید )
درشکل “شماره ۳”دستگاه مختصات قدیم با مبدا O(0,0)کشیده شده است.نقطه O’(x1,y1) موجود می باشد. این نقطه را به عنوان مبدا مختصات جدید در نظر گرفته و مبدا مختصات جدید را رسم می کنیم . حال نقطه ای مانند M(x,y) در دستگاه اصلی(قدیم) در نظر گرفته و مختصات آن را در دستگاه جدید به صورت M(x’,y’) می نویسیم با توجه به شکل شماره ۳ رابطه بین مختصات نقطه M در دستگاه قدیم و جدید به این صورت است :
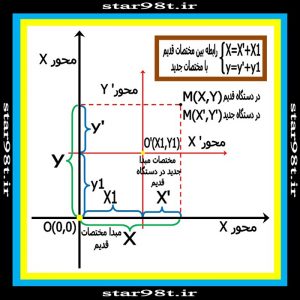
شکل شماره ۳ – انتقال محورهای مختصات

رابطه بین مختصات جدید و قدیم
۴- معادلات گسترده یا ضمنی مقاطع مخروطی
مقاطع مخروطی (دایره ،بیضی ، سهمی و هذولی) همانند هر شکل دیگری در سیستم های مختلف مختصات، معادله جبری مربوط به خودشان را دارند به گونه ای که با رسم این معادلات در سیستم های مختلف می توان آن شکل را بدست آورد . در اینجا معادلات گسترده یا ضمنی مقاطع مخروطی را توضیح می دهیم .
۱) معادلات درجه دوم در سیستم دکارتی
همانطور که گفته شد یک معادله درجه دوم برحسب (yوx) یک معادله جبری است که در آن (yوx) محهول و بقیه حروف در واقع پارامتر یا اعداد مشخص می باشند (در صورتی که اعداد را با پارامتر نشان دهیم تعداد نامحدودی معادله و شکل بدست می آید و در صورتی که بجای پارامتر فقط اعداد مشخص باشند تنها یک شکل بدست می آید ) صورت کلی معادلات درجه دوم بر حسب (x,y) به این صورت است .
![]()
۲) معادلات گسترده یا ضمنی مقاطع مخروطی
معادلات درجه دوم (برحسب x وy)در سیستم مختصات دکارتی به یکی از مقاطع مخروطی تبدیل می شوند یعنی با رسم شکل یک مقطع مخروطی (دایره ، بیضی ، سهمی و هذولی) بدست می آید( اگر در معادله B‡۰ باشدیک مقطع مخروطی مایل بدست می آید که چون مورد نظر ما نیست در همه جا B=0 می باشد ) بنابراین در این قسمت شرایطی را که یک معادله درجه دوم را به معادله ضمنی (گسترده ) یکی از مقاطع مخروطی تبدیل می کند شرح می دهیم . البته شرایطی که برای تبدیل معادله درجه دوم به معادله مقاطع مخروطی در اینجا ذکر می شود شرط لازم می باشد و نه شرط کافی
۳)معادله گسترده دایره
اگر در معادله Ax2+Bxy+Cy2+Dx+Ey+F=0 مقدار A را مساوی C گرفته و B=0 در نظر بگیریم شکل حاصل از آن می تواند یک دایره باشد (شرط لازم برای دایره بودن و البته نه شرط کافی)
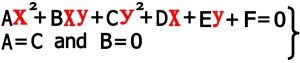
![]()
![]()
نکته ۱ : در زبان ریاضی “and” (یعنی “و” ) به معنی این است که باید هر دو ( یا چند ) شرط با هم برقرار باشد و “or” ( یعنی“یا “ ) به معنی این است که فقط یکی از شرط ها برقرار باشد کافی است .
نکته۲ : بعد از قرار دادن تساوی A=C و B=0 در معادله کلی درجه دوم و جابجا کردن و عوض کردن پارامترها معادله x2+y2+ax+by+c=0 را به عنوان معادله پارامتری و اصلی دایره معرفی می کنیم ولی شکل این معادله به ازاء تمام پارامترهای (a,b,c ) همیشه دایره نیست یعنی می تواند یک نقطه بوده و یا اصولا جواب نداشته باشد ( تهی باشد ) یعنی هیچ شکلی تشکیل نشود در بخش بعدی ( معادله کانونیک مقاطع مخروطی ) این شرط ها را ذکر می کنیم .
۴) معادله گسترده بیضی
اگر درمعادله Ax2+Bxy+Cy2+Dx+Ey+F=0 مقدارB=0درنظر بگیریم و پارامترهای A وCغیر مساوی ولی هم علامت باشند شکل حاصل از آن می تواند یک بیضی باشد(شرط لازم برای بیضی بودن و البته نه شرط کافی)
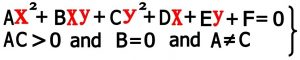
![]()
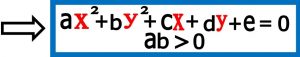
نکته ۱ : این معادله در نهایت بعد از جابجا کردن پارامترها به شکل ax2+ by2+cx+dy+e=0 در می آید که بستگی به مقادیر پارامترها می تواند یک بیضی باشد و یا یک نقطه و یا تهی باشد . ( جواب نداشته باشد)
نکته ۲ : در حقیقت سه نوع بیضی داریم .
۱- بیضی قائم (که قطر بزرگ آن موازی محور Y ها می باشد )
۲-بیضی افقی (که قطر بزرگ آن موازی محور X ها می باشد)
۳- بیضی مایل که قطرهای آن موازی هیچکدام از محورها نیستند .در مورد شرط تبدیل شدن معادله به شکل بیضی قائم یا افقی در بخش بعدی توضیح داده می شود.
تذکر : با قرار دادن B=0 نمی توانیم هیچکدام از مقاطع مخروطی مایل را بسازیم مقاطع مخروطی مایل بعلت پیچیدگی های خودش در این مقاله در مورد آن بحث نمی کنیم. پس همیشه در این مقالهB=0قرار میدهیم .
۵) معادله گسترده سهمی
اگر در معادله Ax2+Bxy+Cy2+Dx+Ey+F=0 مقدار B=0 درنظر بگیریم و از پارامترهای A و C یکی از آنها صفر باشد و دیگری غیر صفر باشد شکل حاصل از آن می تواند یک سهمی باشد (شرط لازم برای سهمی بودن و البته نه شرط کافی) حال با توجه به این که A=0 باشد یا C=0 باشد دو نوع سهمی افقی و قائم بدست می آید و همینطور که بعدا شرح خواهیم داد با توجه به دهانه سهمی به سمت راست و چپ یا بالا و پائین تقسیم می شود. و درکل چهار نوع سهمی بدست می آید که در بخش های بعدی دقیق تر توضیح می دهیم .
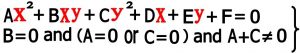
۵-۱) سهمی قائم : سهمی قائم سهمی می باشد که محور آن موازی محور Y ها بوده و خط هادی آن موازی محور X ها باشد . اگر C=0 باشد سهمی قائم بدست می آید .
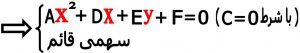

۵-۲) سهمی افقی : سهمی افقی سهمی می باشد که محور آن موازی محور X ها بوده و خط هادی آن موازی محورYها باشد . اگر A=0 باشد سهمی افقی بدست می آید .


۶) معادله گسترده هذولی
اگر در معادله Ax2+Bxy+Cy2+Dx+Ey+F=0 مقدار B=0 در نظر بگیریم و پارامترهای A و C غیر مساوی و هم علامت نباشند شکل حاصل از آن می تواند یک هذولی باشد (شرط لازم برای هذولی و البته نه شرط کافی)
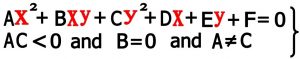
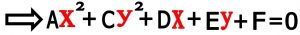
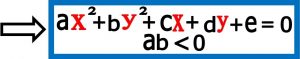
نکته ۱ : این معادله در نهایت بعد از جابجا کردن پارامترها به شکل ax2+ by2+cx+dy+e=0 در می آید که بستگی به مقادیر پارامترها می تواند یک هذولی باشد و یا یک نقطه و یا تهی باشد .
نکته ۲ : هذولی نیز مانند بیضی به دو نوع مایل و افقی تبدیل می شود که در بخش های بعد در مورد آن توضیح می دهیم .
نکته ۳ : همچنین می تواند بجای تشکیل هذولی دو خط متقاطع بوجود بیاید . که در این مورد در بخش های بعدی توضیح خواهیم داد .
۷) خلاصه معادله گسترده مقاطع مخروطی
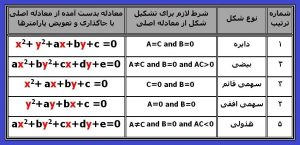
همچنان که دیدیم در معادله Ax2+Bxy+Cy2+Dx+Ey+F=0 با بعضی شرایط می توان معادلات گسترده مقاطع مخروطی(قائم یا افقی)رابدست آورد همه این موارد را درجدول شماره یک خلاصه کردیم .
جدول شماره ۱ – تبدیل معادله Ax2+Bxy+Cy2+Dx+Ey+F=0 به مقاطع مخروطی
۵- معادلات کانونیک مقاطع مخروطی
در سیستم مختصات دکارتی هر مقطع مخروطی معادله مربوط به خودش را دارد که در بخش چهارم شرح داده و خلاصه آن را در جدول شماره یک آوردیم . ولی جدول فوق مشخصات و جزئیات مقاطع مخروطی (مرکز و کانون و خط هادی و…راس) را مشخص نمی کنداز این رو به معادلاتی نیاز داریم تا مشخصات وجزئیات مقاطع مخروطی را مشخص کند . این معادلات را معادله کانونیک مقاطع مخروطی می نامیم .
در این بخش معادلات کانونیک مقاطع مخروطی را فهرست وار و بدون اثبات می آوریم و درجدولی خلاصه می کنیم ولی دربخش های بعد این معادلات را از روی تعریف مقاطع مخروطی به صورت مستقل بدست می آوریم .
۱) معادله کانونیک دایره
معادله کانونیک دایره به این صورت می باشد که در آن C(x1,y1) مختصات مرکز دایره و R شعاع دایره می باشد .
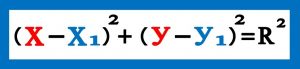
۲) معادله کانونیک بیضی
دو نوع معادله کانونیک بیضی داریم بیضی که قطر بزرگش موازی محور x ها که آن را “بیضی افقی” می نامند و بیضی که قطربزرگش موازی محور yها بوده که آن را بیضی قائم می نامند . در معادلات فوق C(x1,y1) مرکز بیضی می باشد .


۳) معادله کانونیک سهمی
برحسب این که دهانه سهمی کدام طرف باشدچهارنوع سهمی داریم که به ترتیب “سهمی رو به بالا “ ،“سهمی رو به پائین “،“سهمی رو به راست “و “سهمی رو به چپ“ می باشند . علاوه بر این سهمی یک کانون و خط هادی نیز دارد . فاصله بین کانون و راس سهمی را با “P” نشان می دهند ( که عددی مثبت می باشد ) و می توان ثابت کرد که فاصله خط هادی و راس سهمی هم برابر P می باشد یعنی راس سهمی دقیقا در وسط بین خط هادی و کانون قرار دارد . دراین مورد در قسمت بعد که معادله کانونیک سهمی را با توجه به تعریف سهمی بدست می آوریم توضیح می دهیم .

۴) معادله کانونی هذولی
از نظر تعریف هذولی هم شبیه بیضی می باشد طبق تعریف “بیضی مکان هندسی نقاطی است که مجموع فواصلشان از دو نقطه ثابت به نام کانون به یک فاصله باشد” و “هذولی مکان هندسی نقاطی است که اختلاف فاصله اشان تا دو نقطه ثابت به یک فاصله باشد” بنابراین در معادلات کانونیک که برای بیضی می نویسیم کافی است بجای جمع علامت جمع علامت تفریق را وارد کنیم . با این حساب دو نوع هذولی هم داریم . هذولی که دو دهانه آن رو به بالا و پائین می باشد که “هذولی قائم ” ( شبیه بیضی قائم ) و هذولی که دهانه های آن به سمت چپ و راست می باشد که “هذولی افقی “ ( مانند بیضی افقی ) نامیده می شود .


۵) خلاصه مطلب
خلاصه معادلات کانونیک مقاطع مخروطی را می توانیم در جدول شماره ۲ خلاصه کنیم . ولی روش بدست آوردن معادلات کانونیک و همینطور تبدیل معادلات کانونیک به گسترده و برعکس به همراه توضیحات در بخش های ۶ تا ۹ می دهیم .
جدول شماره ۲ – معادله کانونیک کلیه مقاطع مخروطی

نکته : در شکل های این جدول و سایر شکل های بخش ها قسمت های بعد دیده می شود که شکل ها در ربع اول صفحه مختصات (ربع بالا سمت راست ) کشیده می شود . این فقط برای سادگی کار می باشد وگرنه این جدول و شکل ها مربوط به آن می تواند در هر کدام از ربع های صفحه مختصات باشد .
۶- روش بدست آوردن معادله کانونیک دایره و تبدیل آن به معادله گسترده و برعکس
در سیستم مختصات دکارتی هر مقطع مخروطی معادله مربوط به خودش را دارد که در بخش چهارم شرح داده و خلاصه آن را درجدول شماره یک آوردیم . همچنین در بخش پنجم هم معادلات کانونیک مقاطع مخروطی را هم بدون اثبات آورده و خلاصه آن را در جدول شماره ۲ منتشر کردیم . در فصل پنجم تاکید کرده به دلیل طولانی بودن مطلب معادلات کانونیک هر کدام از مقاطع مخروطی را در یک بخش جداگانه با توجه به تعریف آن بدست آورده و همچنین معادلات کانونیک را به گسترده و معادلات گسترده را به کانونیک تبدیل می کنیم و ابتدا از دایره شروع می کنیم .
در این بخش ابتدا معادله کانونیک دایره را به صورت مستقل بدست آورده و همچنین در قسمت بعد معادله گسترده دایره را می نویسیم و با استفاده از اعمال جبری به معادله کانونیک می رسیم . همچنین معادله کانونیک را نوشته و به معادله گسترده می رسیم . بنابراین معادلات کانونیک و گسترده را بهم تبدیل می کنیم .

شکل شماره ۴ – بدست آوردن معادله کانونیک دایره با استفاده از تعریف دایره
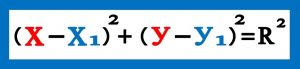
۱) بدست آوردن معادله کانونیک دایره به صورت مستقل و با استفاده از تعریف دایره
برای بدست آوردن معادله کانونیک دایره از روی تعریف یک دایره رسم کرده و مرکز آن را O(x1,y1) می نامیم که یک نقطه کاملا معلوم و مشخصی می باشد . حال به مرکز O یک دایره به شعاع R رسم می کنیم . بنابراین تا اینجا مقادیر R و x1 و y1 کاملا معلوم و ثابت هستند .
طبق تعریف “دایره مکان هندسی نقاطی است که فاصله آنها تا یک نقطه به نام مرکز به یک فاصله باشد .” بنابراین کافی است در روی یک دایره نقطه ای دلخواه به نام P(x,y) انتخاب کنیم ( که مختصات آن مجهول است چون شامل نقاط بیشماری است که محیط دایره را شکل می دهند ) شکل شماره ۴
حال فاصله نقطه P(x,y) را از نقطه O طبق فرمول فاصله بین دو نقطه ( بخش ۳ – قسمت ۴) بدست می آوریم.
۲) بدست آوردن معادله کانونیک دایره از روی معادله گسترده دایره
معادله گسترده دایره به این صورت است : x2+y2+ax+by+c=0 با جابجا کردن جمله های معادله و دسته بندی آن و با استفاده از عملیات جبری ( مانند اتحاد دو جمله ای)سرانجام به معادله :
R2= (x-x1)2+(y-y1)2 می رسیم که معادله کانونیک دایره نام دارد .در این معادله(x1، y1) O مرکز دایره و R شعاع دایره می باشد . بدیهی است معادله در صورتی که R2<0 باشد ( یعنی منفی باشد ) مسئله فاقد جواب و در صورتی که R2=0 باشد تنها یک نقطه می باشد .
۳)مراحل بدست آوردن معادله کانونیک دایره از روی معادله گسترده دایره
در بسیاری از موارد معادله گسترده دایره را داریم و برای بدست آوردن مرکز و شعاع دایره نیازمندیم که معادله گسترده را به معادله کانونیک تبدیل کنیم . مراحل کار به این صورت می باشد .
۳-۱) معادله گسترده دایره : ابتدا معادله گسترده دایره را می نویسیم .

۳-۲) دسته بندی جمله ها : جمله های دارای x و y را از همدیگر جدا می کنیم .
![]()
۳-۳) تبدیل به اتحاد دو جمله ای : نصف ضریب x را به توان دو رسانده و به پرانتزی که حامل جمله های دارای x است اضافه می کنیم و همچنین نصف ضریب y را به توان دو رسانده و به پرانتزی که حامل جمله های دارای y است اضافه می کنیم بنابراین به طرف دوم معادله هم همین مقدار را باید اضافه کنیم همچنین عدد ثابت ( پارامتر c ) را هم به طرف دیگر معادله برده و علامت آن را عوض می کنیم بنابراین داریم .
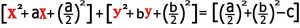
۳-۴) تبدیل به معادله کانونیک دایره : با استفاده از اتحاد دو جمله ای و عوض کردن نام پارامترها نهایتا به این معادله تبدیل شده که معادله کانونیک دایره نامیده می شود .
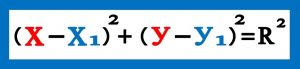
۴) بدست آوردن معادله گسترده دایره از روی معادله کانونیک دایره
همچنین می توانیم به صورت برعکس عمل کرده یعنی معادله کانونیک دایره ”R2= (x-x1)2+(y-y1)2 “ را نوشته و ثابت می کنیم به معادله گسترده تبدیل می شود .
۴-۱) معادله کانونیک دایره : معادله کانونیک دایره ای به مرکز (x1,y1) و به شعاع R را می نویسیم :
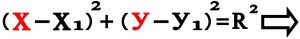
۴-۲) به توان رساندن و دسته بندی کردن : دو جمله را به توان رسانده و دسته بندی می کنیم . ( جملات متشابه را یکجا نوشته و فاکتور گیری می کنیم )
![]()
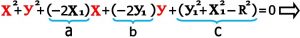
۴-۳) نتیجه گیری نهائی : در آخر همانطور که نشان داده شده مقادیر معلوم را پارامترهای a و b و c نام گزاری می کنیم و به معادله گسترده دایره می رسیم .
![]()
۷- بدست آوردن معادله کانونیک بیضی و تبدیل آن به معادله گسترده و برعکس
در این قسمت ابتدا معادله کانونیک بیضی را فقط با توجه به تعریف بیضی بدست آورده و بعد از روی معادله کانونیک معادله گسترده و از روی معادله گسترده معادله کانونیک را بدست می آوریم . لازم به ذکر است که برای سادگی کار ابتدا مرکز بیضی را مرکز مختصات در نظر می گیریم و بعد با استفاده از روش انتقال مبدا مختصات معادله کانونیک بیضی را در حالت کلی بدست آورده و در مرحله بعد معادله کانونیک را به گسترده و معادله گسترده را هم به کانونیک تبدیل می کنیم .
۱) تعریف بیضی و رابطه بین فاصله کانونی و قطر بزرگ و کوچک بیضی
برای بدست آوردن مستقیم معادله کانونیک بیضی از تعریف بیضی استفاده می کنیم . طبق تعریف
“بیضی مکان هندسی نقاطی از صفحه است که مجموع فاصله های آنها از دونقطه ثابت به نام کانون به یک فاصله باشد . ”
ثابت می شود که این مقدار برابر است با “۲a” که قطر بزرگ بیضی است . بنابراین مجموع فواصل هر نقطه بر روی بیضی از دو کانون برابر است با قطربزرگ بیضی یعنی “۲a” ، همچنین بیضی قطر کوچک هم دارد که با “۲b” نمایش می دهند و فاصله دو کانون را فاصله کانونی نامیده و نصف فاصله کانونی را “۲C” می نامیم و رابطه : “ a2= b2+c2 “ بین قطر بزرگ و کوچک و فاصله کانونی بیضی برقرار است . همچنین محل تقاطع قطر بزرگ و کوچک بیضی را مرکز بیضی می نامیم .
در این قسمت ابتدا معادله بیضی را که مبدا آن مبدا مختصات می باشد بدست آورده و با توجه به فرمول های انتقال مبدا مختصات معادله بیضی که مرکز آن نقطه ای غیر از مبدا مختصات باشد را می نویسیم .
۲) بدست آوردن معادله کانونیک بیضی افقی که مرکز آن مبدا مختصات می باشد
در صفحه مختصات بیضی حالت های مختلفی می تواند داشته باشد . در صورتی که قطر بزرگ بیضی موازی محور X ها (محور طول ها) باشد بیضی را بیضی افقی می نامند . در این قسمت فقط با توجه به تعریف بیضی معادله کانونیک بیضی افقی را بدست می آوریم . برای سادگی کار بیضی را در نظر می گیریم که مرکز آن مبدا مختصات باشد . بنابراین قطر بزرگ بیضی قسمتی از محور Xها (محور طول ها) و قطر کوچک آن قسمتی از محور Yها ( محور عرض ها) می شود و محل تقاطع قطر بزرگ و کوچک هم مبدا مختصات می باشد (شکل شماره ۵) بنابراین با توجه به شکل داریم .
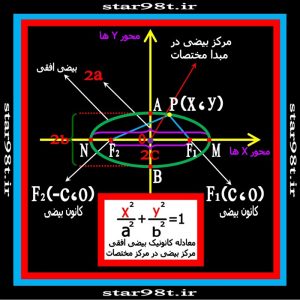
شکل شماره ۵ -بدست آوردن معادله کانونیک بیضی که مرکز آن درمبدا مختصات می باشد .
۱-۲) بدست آوردن فاصله تا کانون ها :
با توجه به شکل شماره ۵ فاصله نقطه دلخواه P(x,y) را از دو کانون “F1” و “F2” بدست آورده و با هم جمع می کنیم .
با توجه به این که مرکز بیضی مبدا مختصات بوده و مقادیر (a,b,c) معلوم و مشخص است و با توجه به تعریف فاصله دو نقطه (بخش ۳ قسمت۴) می توانیم بنویسیم .
![]()
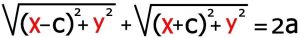
۲-۲) به توان رساندن : بر ای این که رادیکال ها را حذف کنیم باید یکی از رادیکال ها را سمت راست تساوی و دیگری را سمت چپ نوشته و به توان دو برسانیم . بعد از ساده کردن
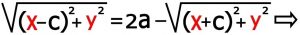
![]()
۲-۳) حاصل عبارت را ساده می کنیم : با استفاده از اتحاد دو جمله ای ضرب ها را انجام داده و معادله را ساده می کنیم ( برای جلوگیری از طولانی شدن مطلب عملیات ساده شدن را توضیح نمی دهیم لطفا برای تمرین هم که شده عملیات جبری را انجام داده تا از معادله بالا به معادله زیر برسید )
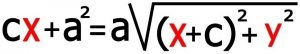
۲-۴) دوباره به توان رساندن : دو طرف معادله را به توان دو رسانده و بعد از ساده کردن (عملیات جبری مربوط را انجام دهید) و با توجه به این که “ b2=a2-c2 ” می باشد سرانجام به این نتیجه می رسیم .

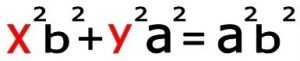
۲-۵) تقسیم دو طرف بر “ a2 b2 ” : دو طرف رابطه را بر “ a2 b2 ” تقسیم می کنیم بنابر این داریم .


۳) بدست آوردن معادله کانونیک بیضی قائم که مرکز آن مبدا مختصات می باشد
بیضی قائم بیضی است که قطر بزرگ آن موازی محور y ها (محور عرض ها ) باشد . در صورتی که مرکز بیضی در مبدا مختصات بوده و قطر بزرگ آن نیز موازی محور طول ها باشد به همان روش که در مورد بیضی افقی شرح داده شد در این مورد هم معادله کانونیک از روی تعریف بیضی براحتی بدست می آید که در اینجا دیگر شرح کامل آن را نمی دهیم .

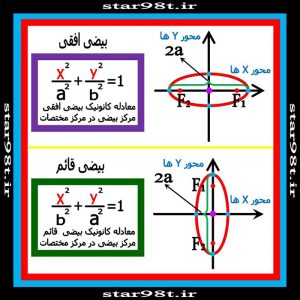
شکل شماره ۶ – بیضی افقی و بیضی قائم در مبدا مختصات
۴) بدست آوردن معادله کانونیک بیضی قائم و افقی که مرکز آن مبدا مختصات نباشد
در مرحله اول معادله بیضی را به صورتی نوشتیم که مرکز بیضی مبدا مختصات می باشد حال همان بیضی را به گونه ای می نویسیم که مرکز آن نقطه دلخواهی به مختصات M(X1,Y1) باشد . برای این منظور ابتدا دستگاه مختصات جدیدی به مرکز M(X1,Y1) با دو محور ‘X و’Y رسم می کنیم . بنابر این معادله بیضی (بیضی قائم و افقی )در این مختصات جدید برابر می شود با :

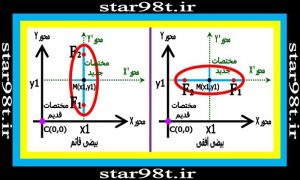
شکل شماره ۷ – انتقال مبدا مختصات و معادله بیضی افقی و قائم
حال معادله بیضی را که در دستگاه مختصات قدیم نوشته بر حسب دستگاه مختصات جدید می نویسیم طبق آن چه از رابطه تبدیل دستگاه مختصات قدیم به جدید داریم (بخش ۴ – قسمت ۸) می توانیم بنویسیم :

و در نهایت نتیجه بگیریم :


۵) تبدیل معادله گسترده بیضی به معادله کانونیک
در این مرحله معادله گسترده بیضی را نوشته و معادله کانونیک آن را بدست می آوریم .
معادله گسترده بیضی به این صورت است.

برای رسیدن به معادله کانونیک به این صورت عمل می کنیم .
۵-۱) عوض کردن پارامترها : در اینجا برای جلوگیری از اشتباه نام پارامترها را عوض کرده و معادله گسترده بیضی را به این صورت می نویسیم .

۵-۲) استفاده از دسته بندی و اتحاد دو جمله ای : با استفاده از دسته بندی و اتحاد دوجمله ای و به همان روشی که در مورد دایره شرح داده شد و همچنین عوض کردن نام پارامترها به این معادله می رسیم .
![]()
۵-۳) تقسیم دو طرف معادله بر P : دو طرف معادله را بر p تقییم کرده همچنین با بردن m و n به مخرج کسر معادله را به این صورت بازنویسی می کنیم .
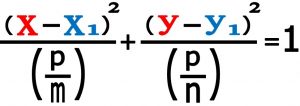
۵-۴) شرط جواب داشتن معادله : اولین شرط جواب داشتن معادله این است که p صفر نباشد در غیر این صورت بجای معادله بیضی تنها یک نقطه بدست می آید .
دومین شرط این است که m و n و p هم علامت باشند. چنانچه m و n هم علامت بوده ولی با p هم علامت نباشند معادله جواب ندارد و اگر m و n هم علامت نباشند معادله جواب خواهد داشت ولی شکل حاصل بیضی نخواهد بود ( هذولی می شود )
۵-۵) معادله کانونیک بیضی افقی : همانطور که خواهیم دید پارامترهای بدست آمده را عوض کرده به گونه ای که معادله کانونیک بیضی مرکز بیضی و قطر بزرگ و کوچک و…پارامترهای بیضی را مشخص کند دو نوع بیضی داریم بیضی افقی که قطر بزرگ آن موازی محور x ها می باشد و بیضی قائم که قطر بزرگ آن موازی محور y ها می باشد در اینجا شرایطی که از معادله گسترده بیضی به بیضی افقی می رسیم توضیح می دهیم .
۵-۶) قطر بزرگ و کوچک و سایر پارامترهای بیضی : در معادله کانونیک بیضی a نیم قطر بزرگ و b نیم قطر کوچک و C(x1 , y1) مختصات مرکز بیضی می باشد با استفاده از فرمول های بیضی فاصله کانونی و خروج از مرکز بیضی را هم می توان براحتی بدست آورد .

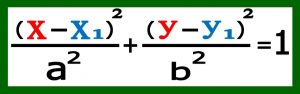
۶) تبدیل معادله کانونیک بیضی به معادله گسترده
در اینجا به روش عکس عمل می کنیم یعنی معادله کانونیک بیضی را نوشته و معادله گسترده بیضی را نتیجه می گیریم . روش کار به این صورت است که در هر دو معادله بیضی ابتدا دو طرف را در a2b2 ضرب کرده و بعد پرانتزها را به توان رسانده و بعد از فاکتورگیری و خلاصه کردن فرمول ها به این نتیجه می رسیم :
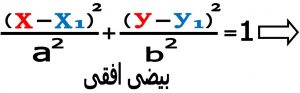
![]()
بعد از بسط دادن و دسته بندی به این نتیجه می رسیم :
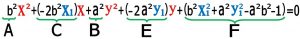
بعد از جاگذاری پارامترها داریم :
![]()
و در نهایت با جابجا کردن پارامترهابه معادله گسترده بیضی می رسیم (ما از بیضی افقی شروع کردیم اگر بجای بیضی افقی بیضی قائم هم بکار ببریم نتیجه فرقی نمی کند کافی است جای a را با b عوض کنیم )

۸-بدست آوردن معادله کانونیک سهمی وتبدیل آن به معادله گسترده و برعکس
در این قسمت ابتدا معادله کانونیک سهمی را فقط با توجه به تعریف سهمی بدست آورده و بعد از روی معادله کانونیک معادله گسترده و از روی معادله گسترده معادله کانونیک را بدست می آوریم . لازم به ذکر است که برای سادگی کار ابتدا راس سهمی را مرکز مختصات در نظر گرفته و بعد با استفاده از روش انتقال مبدا مختصات معادله کانونیک سهمی را در حالت کلی بدست آورده و در مرحله بعد معادله کانونیک را به گسترده و معادله گسترده را هم به کانونیک تبدیل می کنیم .
۱) تعریف بیضی و رابطه بین فاصله کانونی و قطر بزرگ و کوچک بیضی
برای بدست آوردن مستقیم معادله کانونیک سهمی از تعریف سهمی استفاده می کنیم . طبق تعریف
“سهمی مکان هندسی نقاطی از صفحه است که فاصله هر نقطه از آنها از یک نقطه ثابت به نام کانون Fو یک خط ثابت به نام خط هادی سهمی به یک فاصله باشد . ”
این جمله به این معنی می باشد که اگر نقطه ای به نام M(x,y) در روی سهمی در نظر بگیریم فاصله نقطه M از خط هادی و همینطور از کانون مساوی هم باشد و اگر نقطه ای دیگر به نام M’(x’,y’)در نظر بگیریم فاصله نقطه M’هم از خط هادی و کانون مساوی است ولی این فاصله لزوما با فاصله نقطه M ازخط هادی و کانون یکسان نیست .
در این قسمت ابتدا معادله سهمی را که راس آن مبدا مختصات می باشد بدست آورده و با توجه به فرمول های انتقال مبدا مختصات معادله سهمی که مرکز آن نقطه ای غیر از مبدا مختصات باشد را می نویسیم .
۲) انواع سهمی
قبل از شروع بحث معادله کانونیک سهمی ابتدا انواع سهمی را با توجه به دهانه سهمی شرح می دهیم . دهانه سهمی (قسمتی که کانون سهمی در آن قرار دارد و در واقع بخش داخلی سهمی می باشد)برحسب جهت گیری درصفحه می توان به چهارنوع تقسیم کرد(شکل های ۸ تا ۱۱ )
۲-۱) سهمی با دهانه رو به بالا : این یکی از معمول ترین سهمی ها می باشد . راس و خط هادی سهمی را اگر نسبت به محورهای مختصات مقایسه کنیم در پائین و قسمت درونی سهمی رو به بالا قرار دارد .
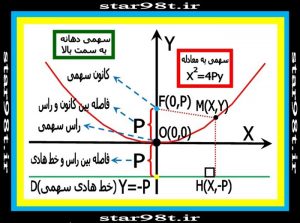
شکل شماره ۸ – سهمی با دهانه رو به بالا
۲-۲)سهمی بادهانه رو به پائین:راس وخط هادی سهمی بالا و قسمت درونی سهمی روبه پائین قرار دارد.
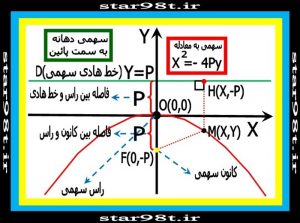
شکل شماره ۹ – سهمی با دهانه رو به بالا
۲-۳)سهمی بادهانه رو به راست:راس وخط هادی سمت چپ و قسمت درونی سمت راست قرار دارد.
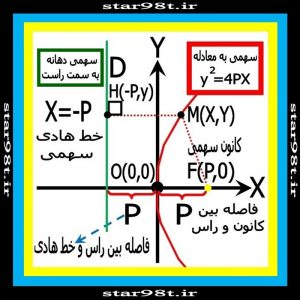
شکل شماره ۱۰ – سهمی با دهانه رو به راست
۲-۴)سهمی بادهانه رو به چپ :راس وخط هادی سمت راست و قسمت درونی سمت چپ قرار دارد.
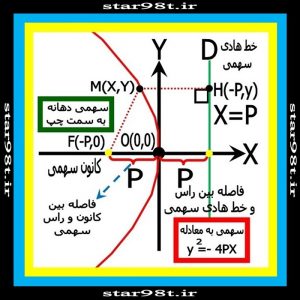
شکل شماره ۱۱ – سهمی با دهانه رو به چپ
۳) بدست آوردن معادله کانونیک سهمی روبه بالا که مرکز آن مبدا مختصات می باشد
همانطور که گفته شدبرای سادگی کار راس سهمی را مبدا مختصات درنظر گرفته و ابتدا معادله کانونیک سهمی را برای سهمی عمودی (با دهانه رو به بالا ) بدست می آوریم .بنابر این با توجه به تعریف سهمی و شکل شماره ۸ داریم .
۳-۱)پاره خط MH : نقطه Mیک نقطه دلخواه با مختصات M(x,y)بر روی سهمی می باشد . از نقطه M بر خط هادی سهمی(خط D)خطی عمود کرده تا خط هادی را درنقطه H قطع کند بنابراین فاصله نقطه Mازخط هادی سهمی ،طول پاره خط MH می باشد نظر به این که خط هادی سهمی موازی محورXها می باشد پاره خط MH با محور Yها موازی بوده و دو نقطه M و H چون هر دو روی خطی موازی محورYها قرار دارد ( مقدار X در هر دو ثابت است) بنابر این طول پاره خط MH برابر است با :
![]()
۳-۲) پاره خط MF : نقطه F کانون سهمی می باشد و چون راس سهمی روی مبدا مختصات قرار دارد کانون سهمی روی محور Yها و با فاصله p از مبدا قرار داشته و مختصات آن عبارت است از F(0,P) بنابر این با توجه به فرمول فاصله بین دو خط ( بخش ۳ قسمت ۴) داریم :
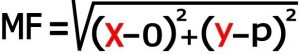
۳-۳) استفاده ازتعریف سهمی :طبق تعریف سهمی فاصله نقطه دلخواه M ازخط هادی و کانون با هم برابر است بنابر این داریم : MF=MH
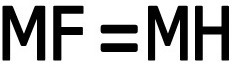
۳-۴) نتیجه نهائی:بعد ازخلاصه و ساده کردن معادله (این کار را انجام دهید) درنهایت داریم .


درمورد انواع دیگر سهمی به همین ترتیب می توانیم معادله کانونیک آن ها را هم بنویسیم(لطفا انجام دهید )

معادله چهار نوع سهمی در مبدا مختصات
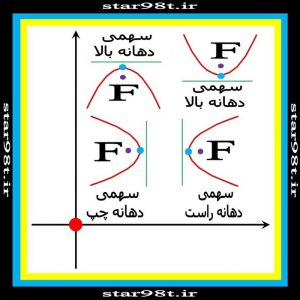
شکل شماره ۱۲ – نگاهی سریع به انواع مختلف سهمی
جدول شماره ۳ – مشخصات انواع سهمی ( راس سهمی در مبدا مختصات )
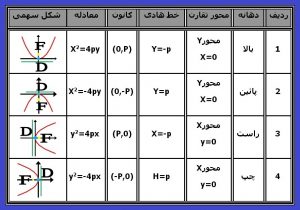
۴) بدست آوردن معادله کانونیک انواع مختلف سهمی با راس دلخواه
به همان طریقی که در مورد بیضی شرح داده شد کافی است . یک دستگاه مختصات با دو محور X وY رسم کرده (دستگاه قدیم) و در داخل این دستگاه دستگاه دیگری با دو محور X’ و Y’(دستگاه جدید) رسم می کنیم و سهمی را به گونه ای در نظر می گیریم که راس آن روی دستگاه جدید (با دو محور X’ و Y’) باشد و با استفاده از فرمول های تبدیل دستگاه جدید به قدیم معادله سهمی را در حالت کلی بدست بیاوریم . در این حالت کانون و معادله خط هادی سهمی نیز عوض می شود . ما این معادله را فقط در مورد سهمی با دهانه رو به بالا انجام داده در مورد انواع دیگر سهمی خودتان انجام دهید .
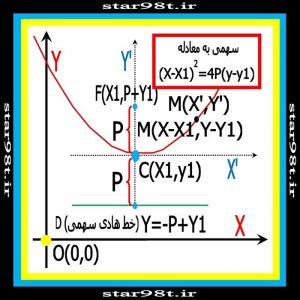
شکل شماره ۱۳ – سهمی با راس غیر از مبدا مختصات

مشخصات سهمی رو به بالا با راس دلخواه
خلاصه مشخصات انواع سهمی که راس آن دلخواه باشد به این قرار است .
جدول شماره ۴ – مشخصات انواع سهمی با راس دلخواه(x1,y1)
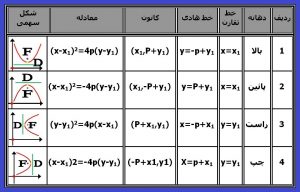
۵) تبدیل معادله گسترده سهمی به معادله کانونیک
در این مرحله معادله گسترده سهمی را نوشته و معادله کانونیک آن را بدست می آوریم .
بنابر این ابتدا این مراحل را طی می کنیم .
۵-۱) استفاده از دسته بندی و اتحاد دو جمله ای : با استفاده از دسته بندی و اتحاد دوجمله ای و به همان روشی که در مورد دایره و بیضی شرح داده شدبه این معادله می رسیم .
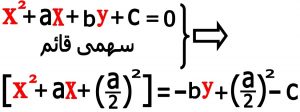
۵-۲)دسته بندی جمله ها:با استفاده از اتحاد دو جمله ای و دسته بندی جمله ها و فاکتور گرفتن از عامل (-۴/b) به معادله زیر می رسیم.
نکته : برای جلوگیری از طولانی شدن مطلب مراحل میانی محاسبات را در اینجا نمی نویسیم می توانید با دنبال کردن محاسبات درستی مراحل فوق را چک کنید و در نهایت به این معادله می رسیم .
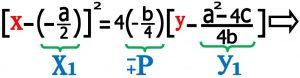
۵-۳) معادله کانونیک سهمی قائم ( دهانه به سمت بالا یا پائین ) : از آنجائی که در معادله کانونیک سهمی پارامتر “P” بسیار مهم و باید مثبت باشد دو حالت در نظر می گیریم .
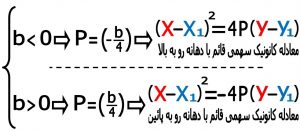
۵-۴)معادله کانونیک سهمی افقی ( دهانه به سمت چپ یا راست ) : همین محاسبات راهم در مورد سهمی افقی انجام داده تا به نتیجه زیر برسیم . لازم به تذکر است برای جلوگیری از طولانی شدن بحث از نوشتن جزئیات معادلات خودداری می کنیم . کافی است در مراحل بالا همه جا جای X را با ٰy عوض کنیم .

نکته : برای جلوگیری از طولانی شدن بحث مثال عددی در اینجا نمی آوریم می توانید مثال عددی هم زده و به همین روش حل کنید .
۶) تبدیل معادله کانونیک سهمی به معادله گسترده
در اینجا به روش عکس عمل می کنیم یعنی معادله کانونیک سهمی را نوشته و معادله گسترده سهمی را نتیجه می گیریم . روش کار شبیه همان روشی می باشد که در مورد بیضی به کار گرفته عوامل مختلف را در هم ضرب کرده و نتیجه را به گونه ای می نویسیم که معادله گسترده از آن ناشی شود( به همین سادگی ) که در اینجا بخاطر طولانی شدن مطلب توضیح نمی دهیم می توانید خودتان بدست بیاورید .
۹- بدست آوردن معادله کانونیک هذولی و تبدیل آن به معادله گسترده و برعکس
در این قسمت ابتدا معادله کانونیک هذولی را فقط با توجه به تعریف آن بدست آورده و بعد از روی معادله کانونیک معادله گسترده و از روی معادله گسترده معادله کانونیک را بدست می آوریم . همانطور که برای سایر مقاطع مخروطی ذکر شد در اینجا هم ابتدا معادله را در مرکز بدست آورده و بعد با توجه به فرمول انتقال مبدا مختصات برای نقاط دیگر هم تعریف می کنیم .
۱) تعریف هذولی و رابطه بین فاصله کانونی و قطر بزرگ و کوچک هذولی
طبق تعریف“هذولی مکان هندسی نقاطی از صفحه است که مجموع فاصله های آنها از دونقطه ثابت به نام کانون به یک فاصله باشد . ” که این مقدار ثابت برابر مقدار برابر است با “۲a” که قطر بزرگ بیضی است .
با توجه به تعریف هذولی مشخص می شود . که هذولی شباهت بسیار زیادی به بیضی دارد با این تفاوت که در بیضی مجموع فواصل مقدار ثابتی می باشد و در هذولی اختلاف فواصل کافی است در معادلاتی که برای بیضی می گذاریم به جای علامت مثبت و یا جمع علامت منفی یا تفریق می گذاریم .
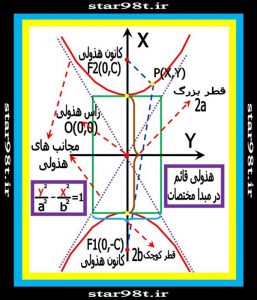
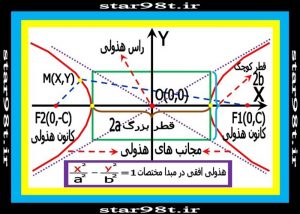
شکل های شماره ۱۴ و ۱۵ – بدست آوردن معادله کانونیک هذلولی که مرکز آن در مبدا مختصات می باشد .
۲) بدست آوردن معادله کانونیک هذولی که مرکز آن مبدا مختصات می باشد
همانند بیضی در صفحه مختصات دو نوع هذولی داریم . در صورتی که قطر بزرگ هذولی موازی محور X ها ( محور طول ها ) باشد هذولی را هذولی افقی می نامند . و اگر موازی محور y ها (محور عرض ها)باشد هذولی را هذولی عمودی می نامند .
در اینجا روش های فوق را توضیح نمی دهیم(زیرا شبیه بیضی می باشد) و فقط به طور اجمالی فرمول ها و محاسبات را ذکر می کنیم .
مطابق شکل شماره ۱۵ نقطه دلخواه M نقطه ای روی هذولی می باشد بنابراین اختلاف فاصله آن از دوکانون مقداری ثابت و برابر قطر بزرگ هذولی “۲a”می باشد بنابراین داریم .
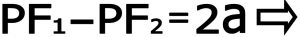
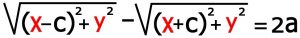
با به توان رساندن رادیکال ها و ساده کردن عبارت های جبری و عملیاتی که شبیه همان بیضی می باشد در نهایت برای هذولی که مرکز آن مرکز مختصات می باشد این معادله ها را بدست می آوریم .


۳) بدست آوردن معادله کانونیک هذولی قائم و افقی که مرکز آن مبدا مختصات نباشد
همانند بیضی و سهمی در مرحله اول معادله را به صورتی نوشتیم که مرکز بیضی مبدا مختصات باشد حال همان معادله را به گونه ای می نویسیم که مرکز آن نقطه دلخواهی به مختصات M(X1,Y1) باشد . برای این منظور ابتدا دستگاه مختصات جدیدی به مرکز M(X1,Y1) با دو محور X’ و Y’ رسم می کنیم . بنابر این معادله هذولی (هذولی قائم و افقی )در این مختصات جدید برابر می شود با :


۵) تبدیل معادله گسترده هذولی به معادله کانونیک
در این مرحله معادله گسترده هذولی را نوشته و معادله کانونیک آن را بدست می آوریم .
معادله گسترده شبیه بیضی می باشد و ما تنها ابتدا و انتهای محاسبات را می نویسیم .
معادله گسترده بیضی به این صورت می باشد .
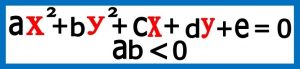
برای رسیدن به معادله کانونیک همانند بیضی با عوض کردن نام پارامترها و استفاده از دسته بندی و اتحادها و… به همان روشی که در مورد بیضی شرح دادیم در نهایت به معادله زیر می رسیم ( دقیقا مانند بیضی )
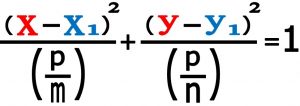
حال شرطی که برای رسیدن به هذولی داریم شبیه بیضی می باشد ، ولی با یک تفاوت کوچک در بیضی m و n و p باید هم علامت باشند ولی در مورد هذولی کافی است p/m با p/n هم علامت نباشند . در این حالت با عوض کردن پارامترها معادله به همان فرم معادله کانونیک هذولی افقی و قائم تبدیل می شود . مثلا تا اینجا ما فرض می کنیم . p و m عددی مثبت و n عددی منفی می باشد همچنین قدر مطلق n از m هم بزرگتر باشد هذولی افقی بدست می آید .
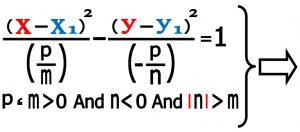

در صورتی که p و n عددی مثبت و m عددی منفی می باشد همچنین قدر مطلق m از n بزرگتر باشد هذولی قائم بدست می آید .
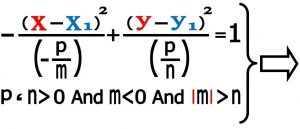

۵) تبدیل معادله کانونیک هذولی به معادله گسترده
در این مرحله معادله کانونیک هذولی را نوشته و بعد از بسط دادن دوجمله ای ها و فاکتورگیری و ساده کردن معادله در نهایت به همان شکل آشنای معادله گسترده هذولی در می آید . نظر به این که روش های به کار رفته بسیار شبیه روش های بکار رفته در تبدیل معادلات کانونیک بیضی به معادلات گسترده می باشد در اینجا از ذکر جزئیات صرف نظر می کنیم شما می توانید به عنوان تمرین مراحل تبدیل را هم انجام بدهید .
۱۰- معادلات قطبی مقاطع مخروطی
در بسیاری از موارد بهتر است بجای معادله منحنی ها در مختصات دکارتی معادله در سیستم قطبی نوشته شود . سیستم مختصات قطبی نخستین بار توسط نیوتن برای اثبات قوانین کپلر به کار گرفته شد . هر چند شواهدی در دست است که نشان می دهد این دستگاه نخستین بار توسط ابوریحان به کار گرفته شده است . در این بخش در مورد سیستم مختصات قطبی و معادله های مقاطع مخروطی در سیستم مختصات قطبی توضیح می دهیم . قبل از آن توضیح کوتاهی راجع به سیستم مختصات قطبی می دهیم .
۱) سیستم مختصات قطبی
در سیستم مختصات دکارتی نقطه ای را به عنوان مبدا مختصات با دو محور در نظر گرفته و مختصات هر نقطه را بر اساس آن دو محور بیان می کنند . در سیستم مختصات قطبی یک نقطه به نام مبدا داشته و بجای دو محور تنها یک محور داریم و مختصات هرنقطه را با فاصله از مبدا و زاویه ای که “پاره خط بین آن نقطه و مبدا مختصات” با محور در جهت خلاف عقربه های ساعت می سازد . اندازه می گیرند بنابراین هر نقطه با یک زوج مرتب تعریف می شود M(r, θ) که در آن r فاصله نقطه از مبدا مختصات و θ زاویه ای است که پاره خط OM (O مبدا مختصات است ) با محور مختصات در جهت خلاف عقربه های ساعت (جهت مثلثاتی ) می سازد .
(در مورد سیستم مختصات قطبی و همینطور کروی در مقاله مفصلی به نام “ سیستم مختصات قطبی “
که بزودی منتشر می شود توضیحات کاملتر را می دهیم .
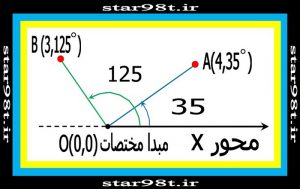
شکل شماره ۱۶ – مختصات قطبی
۲) تبدیل مختصات قطبی به دکارتی و برعکس
با استفاده از فرمول هائی که در این قسمت بیان می شود می توان مختصات قطبی را به دکارتی و برعکس تبدیل کرد.(برای اطلاعات بیشتر راجع به مختصات قطبی و همچنین سایر مختصات و… همچنین تبدیل مختصات قطبی به دکارتی و .. سایر مختصات به مقاله “دستگاه های مختصات در ریاضی “ مراجعه کنید . )
فرمول های تبدیل مختصات قطبی به کارتی به این صورت است .
۱-۲) قطبی به دکارتی : فرمول های تبدیل مختصات قطبی به دکارتی به این صورت است .

۲-۲) دکارتی به قطبی : فرمول های تبدیل مختصات دکارتی به قطبی به این صورت است .

۳) مختصات قطبی مقاطع مخروطی
در سیستم مختصات دکارتی هر شکل هندسی معادله مخصوص خودش را دارد و در سیستم مختصات قطبی هم همینطور مثلا مقاطع مخروطی (دایره ،بیضی،هذولی و سهمی) هم معادله مخصوص به خودشان را دارند که در اینجا بدون اثبات تنها معادلات ذکر شده را آن هم فقط در حالت خاص یعنی حالتی که مرکز (دایره) و یا کانون (سهمی) و یا یکی از کانون ها (بیضی و هذولی) در مبدا مختصات باشند می آوریم . همچنین قطر و یا خط هادی مقاطع مخروطی بایدیا با محور مختصات (تنها محور سیستم قطبی) موازی و یا عمود باشند . حالت های دیگر به دلیل پیچیدگی مربوطه از حوصله این بحث خارج می باشد .
۳-۱) معادله دایره : معادله دایره ای که مرکز آن بر مبدا مختصات منطبق باشد به صورت خیلی ساده برابر است با r=R که در آن “R” شعاع دایره می باشد که بر مرکز مختصات منطبق می باشد .
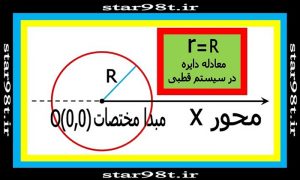
شکل شماره ۱۷ – معادله دایره در سیستم قطبی
۳-۲) معادله بیضی : در سیستم مختصات قطبی معادله بیضی عبارت است از
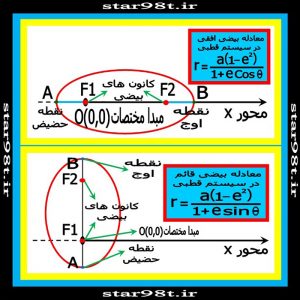
شکل شماره ۱۸ – معادله بیضی درسیستم قطبی
۳-۳) معادله سهمی : معادله سهمی برابر است با
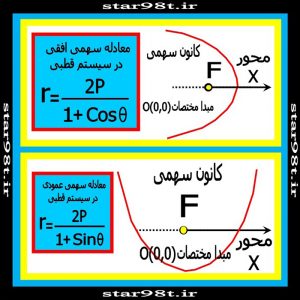
شکل شماره ۱۹ – معادله هذولی در سیستم قطبی
۳-۴) معادله هذولی : معادله هذولی هم به این صورت می باشد .
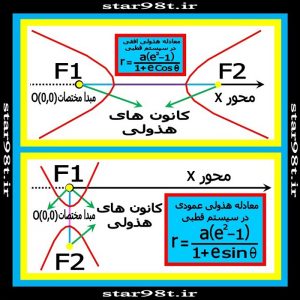
شکل شماره ۲۰ – معادله سهمی در سیستم قطبی
۴) معادله مقاطع مخروطی در سیستم های دیگر مختصات
مقاطع مخروطی و سایر منحنی ها در سیستم های مختصات دیگر (کروی و استوانه ای و جغرافیائی و…)هم دارای معادله مخصوص به خودش می باشد که بعلت پیچیدگی های مربوطه در اینجا دیگر در مورد آن توضیح نمی دهیم .
![]()
برای مطالعه سایر مقاله های نجومی روی شکل زیر کلیک کنید.
![]()
برای مطالعه مقاله های روانشناسی اینجا را کلیک کنید .
![]()
عکس های طبیعت, طبیعت خوانسار , شکوفه های بهاری , گلستان کوه ,دانلود آلبوم های کامل بهترین و زیباترین عکس ها ,آلبوم هائی با صدها عکس کیفیت بالا , در هیچ کجای اینترنت این عکسها را پیدا نمیکنید , عکس هابدون استفاده از تکنیک های فتوشاپ تهیه شده , کاملا طبیعی
![]()
برای آموزش کامل و حرفه ای گوگل مپ روی شکل زیر کلیک کنید
![]()
۱) هر گونه اظهار نظر را در فرم اظهار نظر کاربران وارد کنید .
۲) نظرات بعد از تایید مدیریت نشان داده می شود .
۳) با انتقادات و پیشنهادات سازنده خود ما را هرچه بیشتر همراهی کنید . مدیریت از انتقادات و پیشنهادات سازنده شما استقبال میکند .
۴) نوشته های قرمز پر رنگ ارجاع به لینک هستند که هنوز لینک آنها قرار داده نشده است ( هنوز صفحه آنها منتشر نشده است )
۵) نوشته های آبی پر رنگ ارجاع به لینک هستند که لینک آنها قرار داده شده است ( صفحه آنها منتشر شده است )
۶) هرگونه بهره برداری : کپی تمام و یا قسمتی از مطالب این سایت بدون ارجاع منبع آن ممنوع می باشد .
۷) تکثیر فایل های Pdf با ذکر منبع آزاد ولی فروش آن تحت هر عنوان و با ذکر منبع هم ممنوع می باشد.
![]()