اندازه گیری شعاع زمین یکی از مهمترین اندازه گیری ها می باشد که در نجوم و جغرافیا اهمیت بسزائی دارد و روش های مختلفی درطول تاریخ برای اندازه گیری شعاع زمین به کار رفته که دراینجا به چند روش آن می پردازیم .
۱- روش های اراتستن
نخستين اندازه گيري علمي در حدود سالهاي ۱۹۶ و ۲۷۶ قبل از ميلاد انجام شد. اراتوستن رييس كتابخانه اسكندريه با مشاهده تفاوت زاويه تابش نورخورشيد در۳۱ خرداد در دو شهر مختلف محيط زمين را اندازه گيري نمود.

شکل شماره ۱ – اراتسن
۱)شرح روش اصلی اراتستن
در روز ۳۱ خرداد هر سال(انقلاب تابستاني) در شهر سوئنه در سمت راست رود نيل مصر و نزديك سد اسوان كنوني، خورشيد عمود بر زمين مي تابد و اشياء قائم سايه ندارند. اگر در آن روز كسي در اين شهر در ته چاهي بنشيند خورشيد را هنگام ظهر در بالاي سر خود مي بيند. به عبارتي اجسام در آن زمان سايه ندارند چرا كه اين شهر در نزديكي مدار راس السرطان قرار دارد (طول E34 و عرض N24)
درتاريخ مذكور در كنار دلتاي رودنيل در ساحل جنوب شرقي مديترانه (اسكندريه كنوني) پرتو هاي خورشيد از سمت الراس حدود۷٫۲= ۷,۱۲′ زاويه دارند. يعني در اسكندريه(طول ۳۱E و عرض۳۰٫۴۵N ) يك ميله قائم با پرتوهاي خورشيددر آن تاريخ زاويه مي سازد. از طرفي فاصله اين دو شهر (سوئنه و اسكندريه) ۸۰۳٫۸۴ كيلومتر مي باشد.
اراتوستن با اين اطلاعات توانست شعاع كره زمين را۶۴۰۰km محاسبه نمايدكه با مقدار واقعي آن۳km اختلاف دارد. اگر فاصله دو نقطه را d , اندازه زاویه ای دو نقطه را θ و شعاع زمین را Re در نظر بگیریم داریم :
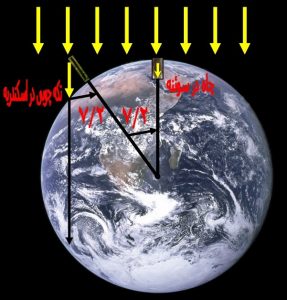

شکل شماره ۲ – وقتی آفتاب در ته چاهی در شهر سوئنه می تابد در شهر اسکندریه زاویه ۷/۲ درجه می سازد
۲) اجرای روش اراتسن برای دو نقطه در یک نصف النهار
برای اجرای این روش لازم نیست حتما در روز ۳۱خرداد(انقلاب تابستانی) باشیم و لازم نیست نقطه ای را پیدا کنیم که هنگام ظهر خورشید در سمت الراس(بالای سر) قرا گیرد. بلکه کافی است دو نقطه را روی زمین درنظر گرفته که دریک نصف النهار باشند و طول جغرافیائی آنها یکی باشد (بنابر این دقیقا درراستای شمال به جنوب جغرافیائی هم قرار دارند) وفاصله آنها را از هم,همچنین ارتفاع خورشید هنگام ظهر را در هر دو نقطه حساب کنیم .
می توانیم یک نقطه را به عنوان نقطه اول انتخاب کرده و مثلادقیقا به سمت شمال جغرافیائی (یا جنوب)حرکت کرده و درحین حرکت فاصله را هم اندازه بگیریم تا به نقطه دوم برسیم ( اگردو نقطه روی جاده ای باشد که شمالی جنوبی باشد می توانیم از کیلومتر شمار ماشین خود هم استفاده کنیم)و در روز بعد ارتفاع خورشید را در هنگام ظهر درهر دو نقطه (به کمک خود و همکارمان ) اندازه بگیریم . هرچه فاصله دو نقطه بیشتر باشد دقت کار بیشتر است . (نگاه کنید به مسیرحرکت خورشید در آسمان)
ارتفاع خورشید در موقع ظهر در هر نقطه به این صورت محاسبه می شود ![]()
که درآن : ارتفاع خورشید= a, عرض جغرافیائی =φ و مایل خورشید = δ
( اثبات کامل این فرمول در روش های اندازه گیری طول و عرض جغرافیائی )
فرمول را می توانیم به این صورت هم بنویسیم :
![]()
بنابر این برای دو نقطه ۱ , ۲می توانیم بنویسیم :
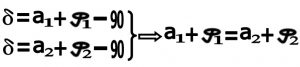
![]()
یعنی برای هر دو نقطه دلخواه روی زمین اختلاف عرض جغرافیائی برابر است با اختلاف ارتفاع خورشید (در موقع ظهر ) در یک روز دلخواه ( برای هر دو نقطه باید یک روز مثلا ۲۰ فروردین باشد ) علامت منفی به این دلیل است که هر چه عرض جغرافیائی بزرگتر ( بالاتر باشد) ارتفاع خورشید موقع ظهر کمتر است.
علت این که دو نقطه را می خواهیم در یک طول جغرافیائی باشند این است که در آن صورت فاصله زاویه ای” θ “ ( در شکل شماره ۳ ) برابر است با اختلاف عرض جعرافیائی φ∇یعنی اختلاف ارتفاع خورشید موقع ظهر a∇- بنابر این داریم .
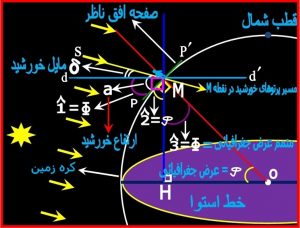
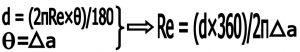
a=90-φ+δ شکل شماره ۳ – اثبات فرمول
با توجه به شکل اثبات بسیار ساده است . اثبات کامل در روش های اندازه گیری طول و عرض جغرافیائی
۳) اندازهگیری محیط زمین در زمان مامون عباسی
با استفاده از روشی که شرح آن داده شد ( اندازه گیری بر اساس اختلاف ارتفاع خورشید برای دو نقطه در یک نصف النهار ) اولین بار در زمان مامون عباسی توسط تعدادی از دانشمندان مسلمان انجام شد . شرح واقعه در کتاب «الزّیخ الکبیر الحاکمی» تألیف ابن یونس مصری متوفی در ۳۹۹/۱۰۰۹ به این صورت شرح داده شده است : «سخن در پیمایش فاصله میان مکانها. در جایی از سند بن علی خواندم که مأمون به او و خالد بن عبدالملک المَروَرّوذی فرمان دادکه اندازه یک درجه ازبزرگترین دوایر سطح کره زمین را اندازه بگیرند(منظور دایره عظیمه است) او گفته است برای این منظور با هم راه افتادیم و علی بن عیسی الاسطرلابی و علی بن الُبخُتری نیز چنین فرمانی دریافتند و به طرفی دیگر به راه افتادند.
سند بن علی میگوید: من و خالد بن عبدالملک به طرف ناحیه میان وامته و وتدمُر رفتیم و در آنجا اندازه یک درجه از بزرگترین دایره مار بر سطح کره ( دایره عظیمه ) را پیدا کردیم که پنجاه و هفت میل شد( هر مایل عربی ۱۹۷۳ متر) ؛ و علی بن عیسی و علی بن البحتری نیز چنین کردند و دو نامه گزارش نتیجه کار از دو ناحیه با هم (به بغداد) رسید و اندازهها با هم موافق بود. (با این روش هر درجه ۱۸۶/۱۱۲ کیلومتر – محیط زمین ۴۰۶۳۰ کیلومتر )
و احمد بن عبدالله معروف به حبش در کتابی از رصدهای مُمتَحَن در دمشق یاد کرده، گفته است که مأمون فرمان داد تا یک درجه از بزرگترین دوایر سطح کره زمین را اندازه بگیرند. برای این منظور در دشت سِنجار چندان پیش رفتند تا اختلاف ارتفاع روز میان دو اندازهگیری در یک روز به یک درجه رسید (اختلاف ارتفاع خورشید دردو نقطه در یک روز )و آنگاه فاصله میان دو مکان را پیمودند که پنجاه و شش میل و ربع شد.
هر میلی چهارهزار ذراع سیاه ( هر زراع سیاه ۴۹٫۳ سانتیمتر ) که مأمون آن را رسمی کرده بود و من به توفیق خدا میگویم که این اندازهگیری مطلق نیست بلکه محتاج آن است که علاوه بر اختلاف دو ارتفاع نیمروزی به اندازه یک درجه، اندازهگیرندگان همگی در سطح یک دایره نصفالنهار بوده باشند( دو نقطه باید روی یک نصف النهار باشند ) و راه کار این است که پس از انتخاب مکانی هموار که همه جای آن را بتوان دید، در نقطهای که اندازهگیری از آن آغاز میشود، خط نصفالنهار را استخراج کنند( مسیری دقیقا در امتداد شمال و جنوب جغرافیائی ) و سپس دو ریسمان باریک و خوب که در ازای هر یک از آنها نزدیک پنچاه ذراع باشد، بگیرند و یکی از آن دو را به موازات خط نصفالنهاری که استخراج شده چندان بکشند تا تمام شود.
و سپس سر ریسمان دوم را بر وسط را بر وسط ریسمان اول قرار دهند( ریسمان دوم را در وسط ریسمان اول قرار دهند ) و بر روی آن صاف بکشند تا تمام شود؛ آنگاه ریسمان اول را بردارند و سر آن را بر ریسمان دوم بگذارند و بر روی آن بکشند تا تمام شود و این کار برای آن است که امتداد (خط نصفالنٌهار) محفوظ بماند و ارتفاع نیمروزی میان مکان اول که خط نصفالنهار در آن استخراج شده و مکان دوم که کار در آن پایان مییابد و تفاوت میان دو ارتفاع نیمروزی در یک روز یک درجه میشود، پیوسته تغییر میکند.
و چون این یک درجه با آلتهای صحیحی که دقایق را نشان میدهد، اندازهگیری شود. اندازه ذراعهایی که میان دو نقطه است طول یک درجه از بزرگترین دوایری است که بر سطح زمین میگذرد و نیز ممکن است که امتداد نصفالنهار را به جای دو ریسمان با سه شاخص نگاه دارند که ابتدا هر سه را بر امتداد نصفالنهار قرار میدهند و سپس آن را که به چشم نزدیکتر است در پشت دو تای دیگر در یک امتداد قرار میدهند و این عمل را به خواست خدا پیوسته تکرار میکنند.
نکته : توضیحات تکمیلی داخل پرانتز و با رنگ آبی قید شده است .
۲- روش پوزی دونیوس
یکی از روش های اندازه گیری شعاع زمین روش فیلسوف و دانشمند یونان باستان پوزی دونیوس بود که بر خلاف دیگران از روی اختلاف ارتفاع ستارگان توانست شعاع زمین را اندازه بگیرد .
۱) پوزی دونیوس که بود
پوسیدونیوس یا پوزی دونیوس ( متولد ۱۳۳ ق . م . در قصبه افامیه از سوریه- ۴۹ ق.م.) از فیلسوفان مشهور یونان است. وی مدت مدیدی در ایتالیا و اسپانیا و ایلیریا و دیگر نقاط سیاحت کرد. آنگاه در ردس اقامت گزید و به تدریس پرداخت و در آنجا چنان مشهور شد که از نقاط مختلف جهان به کلاسهایش میآمدند.
در ریاضی و نجوم و زمین شناسی هم سرآمد عصر خود بود . و مطالعه و کشفیات زیادی داشته مانند :
۱) او نخستین کسی بود که پی برد جزر و مد بر اثر ماه و خورشید رخ می دهد ( توجه کنید زمانی این را اعلام کرد که هنوز قانون جاذبه عمومی شناخته نشده بود )
۲) او همچنین در زلزله و آتشفشان شناسی هم تحقیق و بررسی می کرد و یک جزیره آتشفشانی را در میان جزایر لیبری کشف کرد .
۳) مهمترین دستاورد ش که مدنظر ما می باشد روش اندازه گیری اندازه گیری شعاع زمین از روی ستارگان بود .
۲) روش پوزی دونیوس برای اندازه گیری شعاع زمین
در زمان او فاصله شهر رودس تا اسکندریه را ۶۰۰ کیلومتر(بر حسب واحد های آن زمان که با تبدیل حدود ۶۰۰ کیلومتر می باشد – چون دو نقطه در دریا می باشد با استفاده از طناب های گره دار فاصله را تعیین کرده بودند )
تعیین کرده بودند. (درآن زمان اسکندریه از مهمترین شهرهای روزگار خود بود و خیلی ها به آنجا سفر می کردند)
پوسی دونیوس دریافت که وقتی ستاره ای مانند ( سهیل یا یکی از ستارگان معروف ) در اسکندریه غروب می کند در شهر رودس در ۵/۲۵درجه بالای افق قراردارد . بنابر این اندازه کمانی از دایره عظیمه زمین که بین این دو نقطه وجود دارد ۵/۲۵ درجه می باشند .با توجه به آن که فاصله طولی این دو نقطه ۶۰۰کیلومتر می باشد.بنابر این فاصله یک درجه در روی زمین عبارت است از : ۱۱۴/۲۸۶=۵/۲۵ ÷۶۰۰ یعنی اندازه یک درجه بر روی زمین ۱۱۴/۲۸۶کیلومتر می باشد . پس محیط زمین عبارت است از : ۴۱۱۳= ۳۶۰× ۱۱۴/۲۸۶
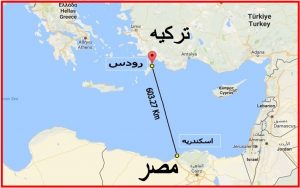
شکل شماره ۴ – موقعیت و فاصله رودس تا اسکندریه
۳) اثبات روش پوزی دونیوس
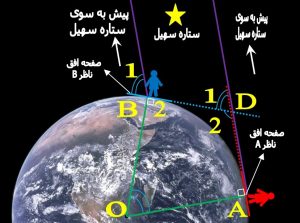
شکل شماره ۵ – اثبات روش پوسی دونیوس
برای اثبات روش پوسی دونیوس کافی است ثابت کنیم در صورتی که یک ستاره (مانند سهیل) در یکی از نقاط ( مانند A) در لبه افق باشد (با ارتفاع صفر ) ارتفاع ستاره در نقطه دیگر ( مانند A ) برابر است با اندازه کمانی که در روی دایره عظیمه زمین آن دو نقطه را بهم وصل می کند یعنی زاویه B1 برابر است با زاویه O
در شکل شماره ۵ داریم :
چهار ضلعی OADB را در نظر گرفته چون مجموع زوایای هر چهار ضلعی ۳۶۰ درجه است داریم :
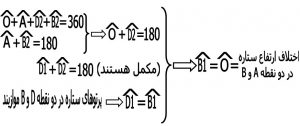
نکته۱ : در همین جا ثابت شدکه زاویه O ( اندازه کمانی از دایره عظیمه زمین که از هر دو نقطه دلخواه می گذرد ) برابر است با مکمل زاویه ای که بین صفحه های افق در دو نقطه فوق وجود دارد .
نکته ۲ : می توان ثابت کرد که اگر ارتفاع ستاره در نقطه A حتی صفر نباشد باز هم زاویه O برابراست با اختلاف ارتفاع ستاره در دو نقطه
نکته ۳ : اختلاف ارتفاع ستاره در دو نقطه خاص برابر است با اندازه کمانی از دایره عظیمه که از دو نقطه می گذرد
۳- روش ابوریحان
این روش توسط ابوریحان بیرونی( تولد ۱۴ شهریور ۳۵۲ وفات۲۲ آذر ۴۲۷ خورشیدی ) منجم و دانشمندمشهور ایرانی وضع شد . ابوریحان با روش جدیدی محیط و شعاع کره زمین را اندازه گرفت . که در کتاب “ قانون مسعودی شرح آن نوشته شده “

شکل شماره ۶- ابوریحان بیرونی
ابوریحان نیز می خواست این کار را در صحرای گرگان(ترکمن صحرا) انجام بدهد اما به دلیل این که دستیار لایق و قابل اعتمادی نداشت از این کار دست کشید تااین که در مسافرتی که به هندوستان داشت در قلعه ای به نام” نندنه” ساکن شد و با روش جدیدی شروع به محاسبه ی شعاع زمین کرد. این دانشمند، در کتاب خود” قانون مسعودی” روش خویش را برای محاسبه ی شعاع کره ی زمین و سپس اندازه گیری محیط آن توضیح داده است.او با روشی علمی و مهندسی چگونگی محاسبه ی شعاع زمین، باکمک تعیین ارتفاع یک کوه را بیان می کند.
۱) روش کار ابوریحان :
روش کار به این صورت است که یک دشت صاف پیدا کرده ( هرچه دشت صاف تر باشد بهتر است یعنی بین نقطه اول و آخر آن اختلاف ارتفاع نباشد) که در انتهای آن یک کوه عظیم (هرچه کوه بلند تر باشد بهتر است , منظور از بلندی ارتفاع کوه ازسطح دشت می باشد نه ارتفاع از سطح دریا ) قرار داشته باشد .
ابتدا ارتفاع کوه را از سطح دشت اندازه می گیریم چون معمولا نمی توانیم ارتفاع کوه را مستقیم اندازه بگیریم ( امروزه به کمک وسائل نوین همچون ارتفاع سنج یا Gps و ابزارهای نوین می توانیم وقتی در دشت هستیم ارتفاع را اندازه گرفته و روی کوه هم همین کار را انجام داده و بعد از هم کم کنیم ولی منظور ما در اینجا روشی است که ابوریحان در آن زمان انجام داد ) از روش مثلث بندی استفاده می کنیم که مفصل شرح می دهیم . ( شکل ۵ )
در مرحله دوم از کوه صعود کرده و زاویه انحطاط افق ( زاویه ای که خط دید ما تا انتهای افق با صفحه افق می سازد ) را بدست آورده ( چون این زاویه با صفحه افقی در واقع منفی است زاویه انحطاط افق نامیده می شود ) و بعد با توجه به آن زاویه شعاع زمین را محاسبه می کنیم . ( شکل شماره ۶ )
۲) روش مثلث بندی برای محاسبه ارتفاع :
در شکل شماره ۷ کوهی در یک دشت قرار دارد می خواهیم بلندی کوه را اندازه بگیریم :
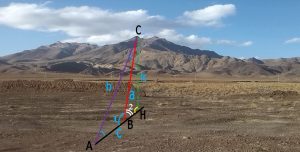
شکل شماره ۷ -روش مثلث بندی برای حاسبه فواصل غیر قابل دسترس
در مسیر حرکت به طرف کوه در نقطه A توقف کرده و زاویه ای که قله کوه (نقطه C ) تحت آن دیده می شود(زاویه A) را اندازه می گیریم . بعد از پیمودن مسیری به نقطه B رسیده و به همان ترتیب زاویه ای که قله کوه تحت آن دیده می شود ( زاویه B2 ) را اندازه می گیریم . (زاویهB1 مکملB2 می باشد, B1=180-B2) در ضمن مسیر نقطه A تا B ( پاره خط AB ) را هم اندازه می گیریم . حال در مثلث ABC با داشتن دو زاویه و ضلع بین نه تنها دو ضلع دیگر بلکه ارتفاع های نظیر اضلاع ( در اینجا ارتفاع CH که همان بلندی کوه می باشد ) را هم حساب می کنیم :
در مثلث ABC داریم .
۲-۱) با داشتن دو زاویه A و B1 زاویه C را هم بدست می آوریم . C=180-(A+B1)
۲-۲) با داشتن سه زاویه و یک ضلع ضلع های مثلث را هم از قضیه سینوس ها بدست می آوریم :
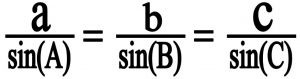
۲-۳) ارتفاع های مثلث را توسط فرمول ارتفاع مثلث بدست می آوریم :
محاسبه مقدار P ( نصف محیط ) :
![]()
محاسبه ارتفاع نظیر ضلع AB:
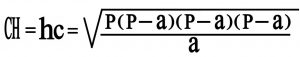
۳) محاسبه زاویه ای انحطاط افق :
آنچه به صورت صفحه افق دیده می شود در واقع یک خطای دید ناشی از کروی بودن زمین است و آن این که انحنای زمین نمی گذارد ما تمام سطح زمین را ببینیم(بدون درنظرگرفتن پستی بلندی ها و کوه ها و…. در اینجا فکر می کنیم وسط دریا و یا دشت کاملا صاف و مسطح ایستادیم ) برای این که این نکته را بهتر متوجه شوید فرض کنید ناظری در روی زمین ایستاده و به جلو نگاه می کند و بخاطر کروی بودن زمین نمی تواند همه جای زمین را ببیند(درست همانطور که در پشت تپه ای کروی ایستاده و نمی تواند همه جای تپه را ببیند) در واقع او (بسته به ارتفاع چشمانش از سطح دشت و یا دریا) می تواند مسافت بسیارمحدودی را ببیند .
اگر ناظر روی درخت یا تپه و…. هر بلندی باشد طبیعتا ارتفاع تپه یا هر بلندی دیگر به ارتفاع دشت افزوده می شود همچنین وقتی این ارتفاعات در فاصه دور باشد باز هم با ارتفاعی که ناظر روی آن ایستاده جمع بسته میشود .
حال فرض می کنیم روی یک کوه بلند ایستاده باشیم و جلو ما دشت صاف قرار دارد که ارتفاع سرتاسرش تقریبا یک اندازه است . چون روی کوه قرار داریم افق ما گسترده تر می شود ( شکل شماره ۶ )
بنابر این در این مرحله از کوه بالا می رویم و روی کوه با ابزارهای اندازه گیری زاویه , زاویه جهت با افق ( C1 ) را اندازه می گیریم . بنابر این در شکل شماره ۶ داریم :
hc ارتفاع کوه که حساب کردیم , Re شعاع زمین , C1 زاویه انحطاط افق که با ابزارهای اندازه گیری زاویه اندازه می گیریم و زاویه C2 متمم زاویه C1 است بنابر این داریم :
با معلوم بودن مقادیر hcوsin(c2) مقدار Re یعنی شعاع زمین هم بدست می آید .
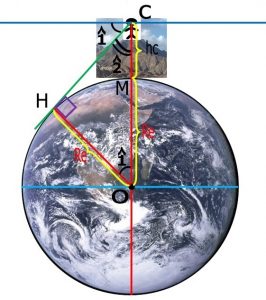
شکل شماره ۸ – محاسبه شعاع زمین به روش ابوریحان
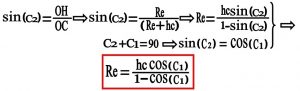
۴) محاسبه محدوده دید
بگذارید قبل از آنکه وارد محاسبات ابوریحان شویم یک اصطلاح جدید را تعریف کرده و مقدار آن را بدست آوریم :
حد دید فاصله چشمان ناظر تا انتهای افق است به علارت دیگر حد دید مشخص می کند ناظری که چشمانش از سطح زمین به اندازه h ارتفاع دارد . تا چه اندازه را می تواند روی زمین ببیند .
حال اگر ناظر کنار دریا یا دشت صاف ایستاده باشد تنها فاصله چشمانش از سطح زمین ملاک قرار می گیرد و در صورتی که روی تپه , درخت ,ساختمان…. یا هر بلندی دیگر ایستاده باشد فاصله چشمانش تا سطح افق معیار قرار می گیرد . و در صورتی که در دور دست ها ارتفاع دشت از قسمتی که ایستاده به اندازه h2 باشد یا بلندی ( کوه , تپه , درخت یا…. ) باشد باز هم این ارقام به ارتفاع دشت اضافه می شود . برای بدست آوردن حد دید می توانیم طول کمانی که بین ناظر تا افق روی سطح زمین است بدست آوریم یا فاصله مستقیم هوائی بین چشم تا آخرین حدی که دیده می شود را حساب کنیم .
با توجه به بزرگی زمین در مقابل اشیاء روی آن تفاوت بسیار اندی بین آنها موجود می باشد(بخصوص وقتی که ارتفاع پائین باشد) برای راحتی کار همان فاصله مستقیم هوائی را ملاک قرار می دهیم .
بنابر این در شکل شماره ۸ داریم :
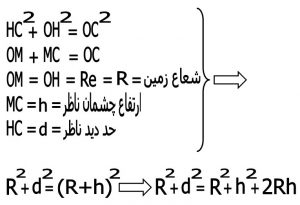
بنابر این داریم

بنابر این محدوده دید برابر است با d=√۲rh اگر شعاع زمین را ۶۳۷۵ کیلومتر بگیریم و h رابخواهیم به صورت متر در نظر بگیریم به طور خیلی ساده فرمول به این صورت تبدیل می شود : d=√۱۲٫۷۵h
که در آن d محدوده دید و h اختلاف ارتفاع بین چشم ناظر و جسم مورد مشاهده می باشد . در صورتی که فاصله این جسم از این حد بیشتر باشد . هیچ قسمتی از جسم رویت نمی شود و در صورتی که کمتر باشد تمام یا قسمتی از جسم دیده می شود .
به عنوان مثال شخصی که فاصله چشمانش از سطح زمین یک ۱/۵ باشد در کنار دریا تا فاصله ۴۳۷۳ متری را می بیند و اگر فاصله چشمانش ۱/۸ متر باشد ۴۷۹۰ متر را می تواند ببیند .
۵) محاسبه ابوریحان :
این دانشمند بزرگوار در آخر کتاب «اسطرلاب» خود فصلی در شناختن اندازه محیط زمین آورده و پس از بیان طریق متعارفی دقیق این اندازهگیری چنین نوشته است:
«و برای دانستن آن روشی ذهنی هست که با برهان صحت آن اثبات میشود ولی عمل کردن آن به علت خردی اسطرلاب و کوچکی مقدار چیزی که بر آن بنا میشود، دشوار است و راه کار آن است که بر قله کوهی مشرف بر دریا بر دشت همواری بالا روی و غروب خورشید را رصد کنی و از این راه مقدار انحطاطی را که گفتیم بدست آوری؛ و ارتفاع کوه را در جیب مستوی(cos) زاویه متمم زاویه انحطاط ضرب کنی وسپس حاصل را برجیب منکوس(۱-cos) خود زاویه انحطاط تقسیم کنی و خارج قسمت را در بیست و دو ضرب و حاصل را بر هفت تقسیم کنی( یعنی عدد پی ) تا از این راه مقدار محیط زمین را بنابر واحدی که با آن ارتفاع کوه را اندازه گرفتهای بدست آوری.
در کتاب «القانون المسعودی» چنین نوشته است:
«در سرزمین هند کوهی را مشرف بر صحرای همواری یافتم که همواری آن همسان همواری سطح دریا بود؛ بر قله آن محل برخورد ظاهری آسمان با زمین یعنی دایره افق را اندازه گرفتم که از خط مشرق و مغرب به اندازه اندکی کمتر از ثلث و ربع درجه انحطاط داشت، و من آن را ۳۴ دقیقه محسوب داشتم سپس ارتفاع کوه را از طریق رصد کردن قله آن از دو نقطه که با مسقط الحجر این قله بر یک امتداد بودند، اندازه گرفتم که مساوی ششصد و پنجاه و دو قله ذراع درآمد… و چون حساب کردم نتیجه تقریباً ۵۸ میل درآمد و از اینجا به صحت اندازهگیری منجمان مأمون اطمینان حاصل کردم.
طبق گفته ابوریحان اندازه قله ۶۵۲ زراع شد و هر زراع هم ۴۹٫۳ سانتیمتر ( یا .۴۹۳ متر ) می باشد زاویه انحطاط افق هم ۳۴دقیقه می باشد بنابر این اندازه شعاع زمین :
hc=652*0.493=321.436m C1=34/60=0.5667 —- درجه — cos(c1)= cos(.5667) =0.99995
بنابر این داریم :
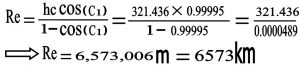
حال طول یک درجه را از روی محاسبات ابوریحان حساب می کنیم

حال اگر در نظر بگیریم که یک مایل ۱٫۹۷۳km یا ۱۹۷۳ متر می شود :
![]()
یا همان ۵۸ مایل می شود .
البته گفته می شود که بعد ابوریحان شعاع زمین را معادل ۶۳۴۰ کیلومتر بدست آورد که با مقدار واقعی آن یعنی (۶۳۷۰ کیلومر ) فقط ۳۰ کیلومتر اختلاف دارد . ولی آنچه در اینجا محاسبه شد حدود ۲۰۰ کیلومتر خطا دارد .
شاید چون کوه بلندی انتخاب نکرده ( ۳۲۱ متر در واقع یک تپه کوچک است ) نتوانسته با دقت بیشتر محاسبه کند .
۴– روش های دیگر اندازه گیری شعاع زمین
بجز روش هائی که شرح آن گذشت روش های دیگری نیز وجود دارد که در اینجا به شرح نمونه هائی از آن می پردازیم .
۱) روش فرنل ( Fernel )
فرنل یکی از پزشکان فرانسوی بود. او در سال ۱۵۲۵در مسیر پاریس(paris) به آمین(Amiens) با بستن دستگاهی به چرخ درشکه خود که شماره دور زدن چرخ را مشخص می کرد توانست فاصله این دو شهر را پیدا کند از طرفی او قبلا طول وعرض جغرافیائی این دو شهر را پیدا کرده بود و پی برد که هر دو شهر در یک طول جغرافیائی قرار داشته و یک درجه اختلاف عرض جغرافیائی دارند . او این فاصله را ۱۱۱ کیلومتر اندازه گیری و بر اساس آن محیط زمین را حدود ۴۰۰۰۰ کیلومتر تعیین کرد که برابر همین مقدار امروزی می باشد . ( شکل شماره ۹)
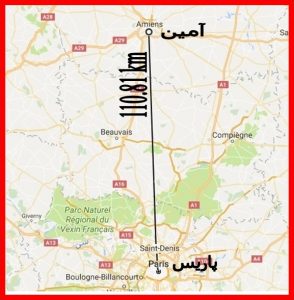
شکل شماره ۹- روش فرنل اندازه گیری فاصله پاریس به آمین
۲) روش ژرژ گاموف (George gamow) و آزمایش بد فوردلول
آزمایش بدفوردلول : اگر در یک تنگه که سطح اب کاملا آرام است سه میله در یک امتداد و به فاصله تقریبی ۱۶۰۹ متر از یکدیگر نصب شود و بعد با دوربین نقشه برداری به آن نگاه شود، نشاهده می شود که راس میله ها در یک امتداد نبوده و میله دوم به اندازه ۱۵ /۲۰ سانتیمتر بالاتر از راس دو میاه دیگر است. این اختلاف ارتفاع به علت آن است که سطح مورد آزمایش کروی است. مسلما با توجه به این اختلاف ارتفاع می توانیم شعاع و ابعاد زمین را محاسبه کنیم.
ژرژگاموف با استفاده از نتایج همین آزمایش و با استفاده از Re=h cosθ/(۱-cosθ)فرمول ( قسمت قبل ) و با اندازه گیری دقیق به کمک نئودولیت توانست محیط زمین را بدقت اندازه گیری کند .
۳) روش آی سینک (i-hsing)
آی سینک ریاضیدان , منجم و راهب بودائی در در قرن هشتم در چین بود او توانست با انجام آزمایشات مختلف بر روی نصف النهار ۱۱۴شرقی به طول ۵۰۰۰کیلومتر(۱۱۴۰۰لی– واحد چینی)محیط زمین را با دقت زیادی تعیین کند.
اساس کار او بر این بود که طول یک شاخص ۹۶/۱ متری ( ۸ فوتی ) در حدود ۰۲/ الی ۰۳/ متر به ازای هر ۱۰۰۰ لی که بر روی مسیر (نصف النهار ) جا بجا می شویم تعغیر می کند با این روش ها او مقدار ۵۶۷۰۰ کیلومتر را برای محیط زمین ارائه داد که با مقدار واقعی آن تفاوت زیادی دارد .
۵- بدست آوردن شعاع زمین به کمک ماهواره
امروزه به کمک ماهواره ها شعاع زمین را در حد سانتیمتر مشخص می کنند روش کار به دو صورت است
۱) محاسبه شعاع زمین از راه تعغیر در سرعت چرخش ماهواره :
سرعت حرکت ماهواره در مدار زمین (مدار کاملا دایره ای ) از فرمول بدست می آید : ( اثبات این فرمول و فرمول های کاملتر در بخش گرانش )
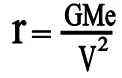
که در آن :
![]()
![]()
![]()
h ارتفاع ماهواره از سطح زمین است ( مبنای سطح زمین نیز ارتفاع از سطح دریا می باشد ) و Re هم شعاع زمین است . بنابر این با اندازه گیری سرعت ماهواره در هر لحظه و ارتفاع ماهواره از سطح زمین می توان شعاع و قطر زمین را در جهات مختلف با دقتی بسیار زیاد بدست آورد ( شکل شماره ۱۰ )
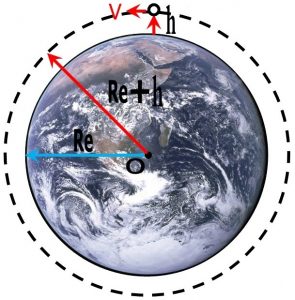
شکل شماره ۱۰ -گردش ماهواره با سرعت لحظه ای V و ارتفاع h از سطح دریا
۲) محاسبه شعاع زمین به روش اراتسن از طریق ماهواره :
در این روش هم مانند روش اراتسن عمل می شود . در واقع در روش اراتسن از راه اختلاف منظر نسبت به خورشید از نقاط مختلف زمین اقدام به اندازه گیری شعاع زمین می کنند . در این حالت ماهواره ها از فضا این عمل را انجام می دهند که در این حالت دو مزیت نسبت به روی زمین دارند
۲-۱) بعلت گردش سریع ماهواره در مدار زمین ماهواره ها می توانند از فاصله بسیار زیادتر از روی زمین این اختلاف منظر را اندازه گیری و بر مبنای ان شعاع زمین را تعیین کنند .
۲-۲) در این روش دیگر نیازی نیست به سمت خورشید نشانه بروند و می توانند به سمت ستارگان دوردست نشانه رفته و اختلاف منظر را از آن طریق حساب کنند . و دقت کار را بالا ببرند .
۳) قطر واقعی زمین :
با استفاده از ماهواره و فناوری های جدید دانشمندان قطر زمین را از جهات مختلف اندازه اندازه گرفتند و متوجه شدند زمین یک کره کامل نیست بلکه قطر استوائی ان از قطر قطبی آن کمی بیشتر است یعنی قطر استوائی ۱۲۷۵۳ کیلومتر و قطر قطبی ۱۲۷۰۹ کیلوتر است که ۴۴ کیلومتر اختلاف دارد ( ۱۲۷۵۳-۱۲۷۰۹=۴۴ ) این مقدار بسیار ناچیز است به طوری که در مقابل اشیائی که فکر می کنیم کاملا گردند مانند توپ فوتبال و… گردتر است .
این را پارامتری به نام تسطیح قطبی معلوم می کند که به این صورت بدست می آید ( Dp قطر استوائی و De قطر قطبی می باشد .
![]()
۶- جمع بندی کلیه روش های محاسبه شعاع زمین
در این قسمت روش های مختلفی برای محاسبه شعاع زمین توسط افراد مختلف از ملیت های مختلف ارائه شد ولی می توان همه آنها را در دو قسمت خلاصه کرد .
۱)روش هائی که بر اساس اندازه گرفتن کمانی از زمین که طول آن معلوم باشد
اگر کمانی از یک دایره داشته باشیم می توانیم محاسبه کنیم که این کمان چه کسری از دایره ای است که کمان جزء آن است از آنجائی که محیط دایره را ۳۶۰ درجه در نظر می گیریم اندازه کمان هم بر حسب درجه تعیین می شود . در حالی که طول کمان همان مسافت طی شده روی کمان است که با واحدهای طول اندازه گیری می شود . برای اندازه گیری محیط دایره اندازه کمان را گرفته معلوم می کنیم که این کمان چه کسری از دایره می باشد و اگر طول کمان را هم داشته باشیم و با یک تناسب ساده محیط دایره بدست می اید :
محیط دایره ( محیط زمین ) / ۳۶۰ = طول کمان( مسافت بین دو نقطه ) / اندازه کمان ( بر حسب درجه )
بر این اساس دو نقطه را که فاصله آنها معلوم بود و یا اندازه گیری می کردند به عنوان طول کمانی از دایره عظیمه زمین در نظر گرفته و اندازه کمان ( این که کمان چه جزئی از این دایره است ) را هم به روش های مختلف اندازه گرفته و بر این اساس محیط زمین را تعیین می کردند .
برای اندازه گیری این زاویه از روش های مختلف همچون : تعغیر طول سایه ها , تعغیر ارتفاع ستاره ها و… استفاده می کردند و یا با تعیین عرض جغرافیا ئی دو نقطه که در یک طول جغرافیائی قرار دارند . مستقیما زاویه را محاسبه می کردند .
۱) اراتستن : بر اساس اختلاف ارتفاع خورشید در دو نقطه این زاویه را اندازه گرفت .
۲) دانشمندان مامون : همانند اراتسن با اندازه گیری ارتفاع خورشید , دو نقطه را که اختلاف عرض جغرافیائی آنها یک درجه بود پیدا کردند .
۳) پوزی دونیوس : اندازه کمان را به کمک اختلاف ارتفاع ستاره ها تعیین کرد .
۴) فرنل : فاصله دو نقطه که طول جغرافیائی یکسانی داشته و اختلاف عرض جغرافیائی آنها یک درجه بود مستقیما با وسیله ای که به کالسکه خود بسته بود اندازه گیری کرد .
۵) آی سینک : با اندازه گیری سایه ها اندازه کمان را پیدا کرد .
۲) مبنای کلی اندازه گیری ها بر اساس تعیین محدوده دید
روش دیگر محاسبه محیط و شعاع کره زمین بر اساس روشی بود که ابوریحان ارائه داد . اساس این روش بر این اصل استوار است که اگر در کنار دریا یا دشت باز ایستاده و به افق مقابل نگاه کنیم بعلت کروی بودن زمین تا یک اندازه محدوده دید داریم اگر زاویه ای که انتهای افق با سطح افقی زمین می سازد اندازه بگیریم براحتی می توانیم با استفاده از فرمول (Re=h cosθ/(۱-cosθ می توانیم شعاع زمین را بدست بیاوریم . در این روش هرچه دشت جلوی ما صاف تر باشد و هرچه ارتفاع ما از سطح دشت بیشتر باشد دقت کار بالاتر می رود . بنابر این بهترین روش نظاره دشت یا دریا در یک کوه بلند و اندازه گرفتن ارتفاع کوه از دشت یا دریا و زاویه θ است .
۱) ابوریحان : اولین بار از این روش محیط زمین را اندازه گیری کرد
۲) ژرژ گاموف : با استفاده از آزمایش بدفوردلول و همان فرمول ابوریحان توانست محیط زمین را اندازه گیری کند .
۳) مبنای کلی اندازه گیری ها بر اساس قوانین جاذبه و روش های مدرن
اساس این روش را در قسمت پنجم این بخش توضیح دادیم .
![]()
برای مطالعه سایر مقاله های نجومی روی شکل زیر کلیک کنید
![]()
برای مطالعه مقاله های روانشناسی اینجا را کلیک کنید .
![]()
عکس های طبیعت, طبیعت خوانسار , شکوفه های بهاری , گلستان کوه ,دانلود آلبوم های کامل بهترین و زیباترین عکس ها ,آلبوم هائی با صدها عکس کیفیت بالا , در هیچ کجای اینترنت این عکسها را پیدا نمیکنید , عکس هابدون استفاده از تکنیک های فتوشاپ تهیه شده , کاملا طبیعی
![]()
برای آموزش کامل و حرفه ای گوگل مپ روی شکل زیر کلیک کنید
![]()
۱) هر گونه اظهار نظر را در فرم اظهار نظر کاربران وارد کنید .
۲) نظرات بعد از تایید مدیریت نشان داده می شود .
۳) با انتقادات و پیشنهادات سازنده خود ما را هرچه بیشتر همراهی کنید . مدیریت از انتقادات و پیشنهادات سازنده شما استقبال میکند .
۴) هرگونه بهره برداری : کپی تمام و یا قسمتی از مطالب این سایت بدون ارجاع منبع آن ممنوع می باشد .
۵) تکثیر فایل های Pdf با ذکر منبع آزاد ولی فروش آن تحت هر عنوان و با ذکر منبع هم ممنوع می باشد .
![]()