روش های اندازه گیری های غیر مستقیم فاصله

بسیاری از اوقات  طول هائی که می خواهیم در روی زمین اندازه بگیریم و به آنها دسترسی نداریم مثلا یا دور دست هستند یا مانعی بین آنها و ما وجود دارد (مانند رودخانه ) و به هر دلیل ترجیح می دهیم به طور غیر مستقیم آنها را اندازه گیری کنیم .

۱– مثلث بندی و حل مثلث

در این گونه مواقع از روش مثلث بندی استفاده می کنیم . در یک مثلث با داشتن بعضی از اجراء آن (اجزاء اصلی و فرعی مانند ضلع ها و زاویه ها و ارتفاع ها و…) به کمک فرمول های مثلثاتی می توانیم اجزاء دیگر را بدست آوریم .
نظر به این که اندازه گیری زاویه همیشه راحت تر از اندازه گیری ضلع است ( بخش روش های اندازه گیری زاویه را مطالعه کنید ) بنابر این سعی می کنیم مثلا در مثلث حداقل یک ضلع ( که اندازه گیری آن راحت تر است) را اندازه گرفته و بعدزاویه های مورد نیاز را و به کمک فرمول های مثلثاتی بقیه اجزاء را بدست بیاوریم .
برای بدست آوردن فرمول ها به مقاله 🙁 بدست آوردن اجزاء مجهول مثلث به کمک اجزاء معلوم مراجعه کنید )

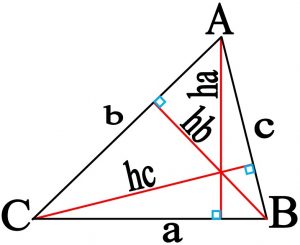
شکل شماره ۱  -مثلث ABC  و ارتفاع هایش

۲- پیدا کردن فاصله با یک جسم با رصد جسم از دو نقطه مختلف

فرض کنیم می خواهیم فاصله خود را تا یک جسم دور دست  اندازه بگیریم و بعلت موانع (مثلا یک رودخانه) یا به هر دلیل دیگر ( مثلا دوری فاصله ) نمی توانیم مستقیم به سمت آن جسم حرکت کنیم . پس باید به صورت غیر مستقیم اندازه گیری را انجام دهیم . کافی است مسیری مستقبم و قابل اندازه گیری که حتی الامکان به سمت جسم نباشد انتخاب کرده و ازدو نقطه درمسیر جسم را رصدکنیم.( مرجعه به مقاله روش های اندازه گیری زاویه )
در شکل شماره ۲ این کار توسط دو نفر ( آقا و خانم ) در دو نقطه A و B  انجام می شود هر کدام از دو تیر چوبی استفاده می کنند(دو تیر چوبی برای دقت بیشتر ) که نوک تیرها و جسم باید در راستای هم قرار داشته باشند . و به صورتی که در شکل دیده می شود مسیر AB و  زاویه هایA و  Bرا اندازه گرفته  , در این حالت مثلث ABC با دو زاویه و ضلع بین قابل اندازه گیری می باشد و اضلاع AC و BC هم بدست می آید . ( فرمول سینوس ها )

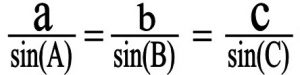
شکل شماره ۲ – بدست آوردن فاصله به روش غیر مستقیم

۳- پیدا کردن بلندی کوه با رصد از دو نقطه مختلف  

فرض کنیم در یک دشت در حال حرکت به طرف یک کوه هستیم و می خواهیم قبل از رسیدن به کوه بلندی کوه را از سطح دشت اندازه بگیریم . ( شکل شماره ۳)
در مرحله اول در یک نقطه توقف کرده (نقطه A) زاویه ای که نوک قله با سطح افق می سازد اندازه می گیریم( به روش تیرهای چوبی نیز می توانیم زاویه را اندازه بگیریم که دیگر آنها را رسم نکرده ایم ) حال در نقطه ای دیگر (نقطه B) همین کار را می کنیم و فاصله AB را هم اندازه می گیریم .
۱) در مثلث  ABC طول ضلع های مثلث یعنی a,b,c را  با توجه به فرمول سینوس ها بدست می آوریم  (دقت کنید زاویه نظیر ضلع B در مثلث در واقع زاویه B2 می باشد کافی است زاویه اندازه گرفته شده “B1” را از ۱۸۰ کسر کنیم  ( دقت کنید مثلث تشکیل شده همیشه منفرجه الزاویه بوده و ارتفاع خارج مثلث قرار دارد )

حال کافی است در مثلث ABC ارتفاع نظیر راس C را حساب کنیم با توجه به فرمول ارتفاع :

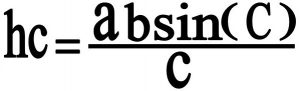
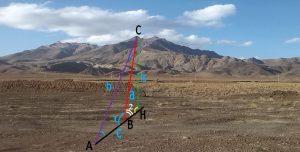
شکل شماره ۳ – بدست آوردن بلندی کوه به روش غیر مستقیم

۴-  اندازه گیری عرض یک جسم

در شکل شماره ۱۷ می خواهیم عرض رشته کوه را اندازه بگیریم . به ترتیب این کارها را انجام می دهیم .
۱) فاصله AC و BC را مطابق روشی که در شکل شماره ۱۵ شرح داده شد بدست می آوریم .
۲)  حال زاویه C را بدست می آوریم (می توانیم به روش تیرهای چوبی و یا با استفاده از وسائل مخصوص اندازه گیری زاویه  – مقاله روش های اندازه گیری زاویه )
در این صورت خیلی راحت با استفاده از فرمول کسینوس ها ( مراجه شود به بدست آوردن اجزاء مجهول مثلث به کمک اجزاء معلوم ) می توانیم فاصله محهول را بدست آوریم (در اینجا cضلع روبرو به راویه Cیعنی AB است ).

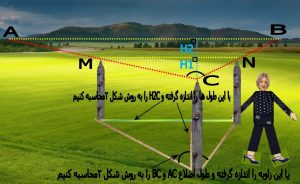
شکل شماره ۴ – به دست آوردن عرض رشته کوه با داشتن فاصله از رشته کوه

ولی یک کار ساده تر می توانیم بکنیم . دو تکه چوب که در نقطه M و N وجود دارد به گونه ای تنظیم می کنیم که راستای آنها موازی راستای جسم شوند یعنی در شکل شماره ۴ داریم : MN موازی AB شود
در این صورت بجای محاسبه طول اضلاع BC وAC کافی است فاصله عمودی تاAB ( پاره خط CH2) را به روش شکل شماره ۲ محاسبه کرده در این صورت  بعد تنها باید CH1 ( طول خطی که از نقطه C بر امتداد MN عمود می شود ) و MN ( فاصله دو تیرک چوبی)را اندازه گیری کنیم .( اندازه گیری طول های MN و CH که بصورت مستقیم متر می کنیم بسیار ساده تر از اندازه گیری فاصله هائی نظیر AC و BC است که دور از دسترسند )

روش کار به این صورت است :
در شکل شماره ۴ دو مثلث MNC و ABC متشابهند زیرا ( MN موازی AB می باشد ) همچنین پاره خط CH2 بر هر دو خط عمود است بنابر این داریم :

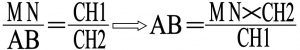
۵- اندازه گیری عرض یک جسم با داشتن فاصله و زاویه دید

این موضوع که ما فاصله از یک جسم را داشته باشیم و بتوانیم با اندازه گیری زاویه ای که جسم تحت آن دیده می شود بتوانیم جسم را اندازه بگیریم بسیار مهم است .
در نقشه برداری و نجوم و مهندسی موارد زیادی پیش می آید که فاصله و زاویه ای که یک جسم دور دست تحت آن دیده می شود را به روش های مختلف (دوربین های فاصله یاب و زاویه یاب)اندازه بگیریم همچنین به روش های مختلف فاصله ماه تا زمین و خورسید تا زمین و فاصله اجسامی که دارای قطر هستند(و یا فاصله زاویه ای دو جسم مجزا ) را تعیین کرده و حال با اندازه گیری زاویه ای که تحت آن دیده می شود می خواهیم اندازه جسم ( فاصله دو جسم مجزا ) را اندازه گیری کنیم . ( شکل شماره ۵ )

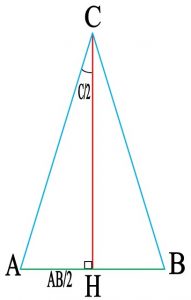
شکل شماره ۵ – به دست آوردن قطر جسمی که فاصله آن معلوم است .

با توجه به شکل شماره ۵ فاصله AH بدین گونه بدست می آید ( فاصله از جسم را h و قطر جسم  را D نام گذاری می کنیم ) با توجه به شکل شماره ۱۶ داریم : ( CH=h   و   AB=D  )

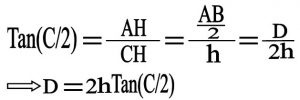
 در مورد اشیاء بسیار دور همچون ستارگان و… زاویه دید بسیار کوچک می شود و بنابر این مقدار tan(و همچنین sin)زاویه با خود زاویه بر حسب رادیان برابر می شود . همچنین تفاوتی بین BC و AC (در شکل ۵) و ارتفاع وارد بر ضلع AB یعنی CH وجود ندارد  .

۶-   اندازه گیری های غیر مستقیم بدون اندازه گیری زاویه

در تمام این اندازه گیری هائی که تا اینجا ذکر آن رفت حداقل یک زاویه را باید اندازه گیری می کردیم بدون وسائل کافی اندازه گیری زاویه سخت از اندازه گیری مسافت های در دسترس است . در اینجا روشی ارائه می شود که بتوان فاصله تا جسمی دور و غیر قابل دسترس را تنها با اندازه گیری فاصله اندازه گرفت . ( شکل شماره ۶ )

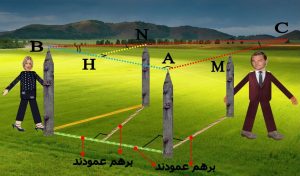
شکل شماره ۶ – محاسبه فاصله تا جسم دور دست بدون اندازه گیری زاویه

روش کار به این صورت است :
۱) ابتدا از نقطه A ( تیرک A ) جسم دور دستی  که در نقطه C قرار دارد به گونه ای رصد می کنیم که نوک تیرک A وM و C بر یک امتداد باشند (تیرک M فقط برای بالابردن دقت است و کاربرد دیگری ندارد )
۲) تیرک واقع در نقطه B را به گونه ای انتخاب می کنیم که AB در امتداد عمود بر AC با شد. یعنی مثلث ABC قائم الزاویه باشد .
۳) تیرک واقع در نقطه N را به گونه ای انتخاب می کنیم که B و N و C  در یک راستا باشد .
۴) از نقطه N خطی بر AB عمود کرده پای عمود را H گذاشته و فاصله آن را اندازه می گیریم . (مثلثBHN  هم قائم الزاویه است)
دو مثلث قائم الزاویه BHN و BAC با هم متشابهند زیرا در راس B مشترکند . بنابر این داریم :

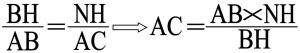
برای مطالعه سایر مقاله های نجومی روی شکل زیر کلیک کنید

برای مطالعه مقاله های روانشناسی اینجا  را کلیک کنید .

عکس های طبیعت, طبیعت خوانسار , شکوفه های بهاری  , گلستان کوه ,دانلود آلبوم های کامل بهترین و زیباترین عکس ها ,آلبوم هائی با صدها عکس کیفیت بالا ,  در هیچ کجای اینترنت این عکسها را پیدا نمیکنید , عکس هابدون استفاده از تکنیک های فتوشاپ تهیه شده , کاملا طبیعی 

برای آموزش کامل و حرفه ای گوگل مپ روی شکل زیر کلیک کنید

همه جیز در مورد گوگل مپ

۱) هر گونه اظهار نظر را در فرم اظهار نظر کاربران وارد کنید .
۲) نظرات بعد از تایید مدیریت نشان داده می شود .
۳) با انتقادات و پیشنهادات سازنده خود ما را هرچه بیشتر  همراهی کنید . مدیریت از انتقادات و پیشنهادات سازنده شما استقبال میکند .
۴) هرگونه بهره برداری : کپی تمام و یا قسمتی از مطالب این سایت بدون ارجاع منبع آن ممنوع می باشد .
۵) تکثیر فایل های Pdf با ذکر منبع آزاد ولی فروش آن تحت هر عنوان و با ذکر منبع هم ممنوع می باشد .