قانون جاذبه عمومی نیوتن

گرانش یکی از نیروهای بنیادی جهان است که تاکنون ماهیت کامل آن مشخص نشده است . گرانش در کنار سه نیروی دیگر (نیروی هسته‌ای ضعیف، نیروی هسته‌ای قوی، نیروی الکترومغناطیسی ) ساختار جهان ما را شکل داده است . در این مقاله در مورد نیروی گرانش و ماهیت آن توضیح می دهیم . قبل از آن مروی می کنیم به آنچه در این فصل ( فصل گرانش )  تاکنون در مورد نیروی گرانش گفته ایم .

۱- تاریخچه گرانش

در این بخش به طور خیلی خلاصه در مورد تاریخچه گرانش و این که چگونه بشر به نیروی گرانش پی برد و آن را بر اساس فرمول های ریاضی نوشت می پردازیم .
برای مطالعه کامل به مقاله های “ تاریخچه گرانش “ مراجعه کنید .

۱) تاریخچه گرانش قبل از کپرنیک

مردمان باستان هیچگونه درکی از گرانش نداشتند چون از نیرو نیز درکی نداشتند . ارسطو فکر می کرد برای ادامه حرکت یک جسم باید همواره نیروئی به جسم وارد شود برای همین طلوع و غروب و حرکت هماهنگ ستارگان از شرق به غرب برای آنها اسرار آمیزبود(همچنین حرکت سیارات در بین ستارگان) ازاین رو اینگونه پدیده ها را با روش های خرافی و …توجیه می کردند.فیلسوفان یونان فکر کردند که اجرام آسمانی بخشی از قلمرو خدایان هستند و دنبال “حرکت طبیعی” برای آنها می گشتند. آنها متوجه نشدند که در واقع درگیر نیروی گرانش هستند . اسرار آمیز بودن فضا و اجرام سماوی موجب شد که فکر کنند ستارگان و سیارات بر روی زندگی بشر تاثیر گذاشته و از این رو طالع بینی را بوجود آوردند و از طریق طالع بینی (که آن زمان علم نامیده می شد) به پیش بینی آینده و…بپردازند.خرافه ای که متاسفانه تا امروز نزد بسیاری از مردم جاهل ادامه دارد .
سرانجام بطلمیوس بر اساس گردش ستارگان به دور زمین (که می دانیم ناشی از حرکت وضعی زمین می باشد) و حرکت سیارات در لابلای ستارگان نظریه زمین مرکزی را وضع کرد که ۱۵۰۰سال برعلم ستاره شناسی سلطه داشت و چون کلیسا به عنوان یک اصل پذیرفته بود جنبه مذهبی هم پیدا کرد .

۲) کپرنیک و نظریه زمین مرکزی

انقلاب علمی با انقلاب در نجوم و با نظریه نیکلاکپرنیک آغاز شد. کپرنیک در سال۱۴۷۴در لهستان بدنیا آمدبعد از تحصیلات مقدماتی کپرنیک برای ادامه تحصیل علوم دینی به ایتالیا رفت سرانجام درسال ۱۴۹۷به مقام اسقفی رسید او به دانشگاهی در لهستان که علوم مذهبی و ریاضیات تدریس می کردند رفت . در همان دانشگاه بود که معلم کپرنیک او را با نجوم و ستاره شناسی آشنا کرد و کپرنیک عاشق ستاره شناسی شد . او در سال های ۱۵۱۹تا ۱۵۲۴فرماندهی شهر مرزی “ آلنشتاین “را عهده گرفت و در این ایام بود که به خواندن و مطالعه دروس نجومی پرداخت . او رصدخانه ساده ای ساخته و در آن رصدخانه به مطالعه در باره حرکات اجرام آسمانی پرداخت و آن را با جدول‌های نجومی قدیمی مقایسه می‌کرد . در همانجا بود که کپرنیک با مقایسه جداول نجومی و رصدهائی که خودش انجام داده بود به این نتیجه رسیدکه نظام بطلمیوسی ایرادهای بسیاری دارد و برای برطرف کردن این ایرادها تنها راه این است که بجای زمین خورشید را مرکز عالم قرار دهدو بدین ترتیب کپرنیک نظریه خورشید مرکزی را در کتابی به نام “دربارهٔ گردش افلاک آسمانی “ منتشر کرد و با مخالفت جدی اربابان کلیسا مواجه شدهزاران نفر به جرم دفاع از نظریه کپرنیک محاکمه و زندانی شده و حتی در آتش زنده زنده سوزانده شدند با این وجود بعد از حدود ۲۰۰ سال نظریه کپرنیک جای نظریه زمین مرکزی را گرفت .

۳) گالیله  

کپرنیک اولین جرقه را زد و اولین تحول را درتاریخ ستاره شناسی ایجاد کرد ولی قبل از آن که همه حقایق آشکار شود لازم بود تعغیرات اساسی در نگرش به علم ایجاد شود عامل و بانی این تعغیرات کسی نبود بجز گالیله دانشمند ایتالیائی، گالیله نگرشی نو به علم فیزیک و علوم تجربی ایجاد کرد و نشان داد که سنگ بنای اصلی علوم تجربی ، تجربه و آزمایش است و بر خلاف پیشنیان که عقیده داشتند دانشمند نباید کار تجربی انجام دهد گالیله عقیده داشت دانشمند باید کار تجربی انجام دهد و در حقیقت سنگ بنای علوم را با تجربه و آزمایش بنا کرد . او فیزیک را به عنوان شاخه ای مجزا و به عنوان یکی از علوم تجربی به جهانیان معرفی کرد و پایه و اساس کار فیزیک را تشریح قوانین و پدیده های طبیعت به کمک فرمول های ریاضی دانست . نقش گالیله در رنسانس علمی و پیشبرد دانش فیزیک و نجوم بر کسی پوشیده نیست ( ما در مقاله “ تاریخچه گرانش “ بخش سوم  ۳- گالیله پدر فیزیک نوین ) به طور کامل در این زمینه توضیح دادیم .

۴) کپلر و تیکو براهه

تیکو براهه (Tycho Brahe) درسال۱۵۴۶درشهر استورپ دانمارک از یک خانواده ثروتمند و مشهور بدنیا آمد. تیکو براهه بزرگترین رصدگری بود که دنیا تا آن روز دیده بود او سیارات را آنطور که از زمین دیده می شوند دید و تمام اطلاعات را ثبت کرد. در همان زمان تیکو براهه ،دانشمند دیگری در آلمان به نام یوهانس کپلر( متولد ۲۷دسامبر ۱۵۷۱) زندگی می کرد . کپلر دانشمند، ریاضیدان و ستاره‌شناس مشهوری بود. در سال۱۶۰۰که تیکوبراهه به آلمان آمد و منجم سلطنتی آلمان شدکپلر را که بسیار مشهور شده بود به عنوان دستیار خود انتخاب کرد . در اواخر سال ۱۶۰۱تیکوبراهه بر اثر سکته مغزی درگذشت وکپلر نه تنها جانشین تیکو براهه شد بلکه وارث تمام جداول نجومی و کارهای تیکو براهه شد و با مطالعه روی جداول نجومی سه قانون خود را نتیجه گیری کرد که به نام قوانین کپلر شناخته می شود .

۵) ظهور نیوتن

سِر ایزاک نیوتن(Sir Isaac Newton)در ۲۵دسامبر۱۶۴۲(در همان سال مرگ گالیله) در روستای « وولستورپ » از توابع شهرلینکولنشیز انگلیس بدنیا آمد.(درباره زندگی نیوتن و کشفیات او درمقاله “زندگی نامه نیوتن” توضیح کافی خواهیم داد) نیوتن با وجود این که یتیم بود و وضع مالی خوبی نداشت مدارج ترقی را بسرعت طی کرد و توانست از استادی دانشگاه تا رئیس ضرابخانه سلطنتی و ریاست انجمن سلطنتی و… رسیده و در موارد بیشماری (فیزیک نور ، قوانین حرکت ، فرمول بندی قانون جاذبه عمومی و… حساب دیفرانسل و انتگرال ) خدمات شایسته ای به جهان علم و جامعه بشری ارائه کند . ولی مهمترین دستاوردی که او را به شهرت جهانی رساند همان قانون جاذبه عمومی بود . او مجموعه کشفیاتی که در زمین های مختلف مکانیک ( قوانین حرکت و گرانش ) بدست آورده بود در کتابی به نام “ اصول ریاضی فلسفه طبیعت “ در ۵ ژوئیه ۱۶۸۷ با سرمایه ادموندهالی (دانشمند بزرگ )منتشر کرد.

۶) بعد از نیوتن

مطالب و قوانینی که نیوتن کشف کرده و در کتاب اصول خود آورده بود علم فیزیک و مکانیک را دگرگون کرد به گونه ای که تا حدود ۲۳۰ سال تمام معلومات بشری در مورد مکانیک ( علم حرکت ) همان بود که نیوتن در کتاب اصول خود آورده بود و به نام مکانیک کلاسیک و یا مکانیک نیوتنی خوانده شد و تنها بعد از ظهور نظریه های نسبیت و کوانتم معلوم شد که مکانیک نیوتنی (مکانیک کلاسیک) تنها حالت خاص مکانیک کوانتمی نسبیتی می باشد .

۲- چگونه نیوتن قانون جاذبه عمومی را کشف کرد

تا زمان نیوتن بسیاری از مسائل در ارتباط با قانون جاذبه عمومی شناخته شده بود و همه این ها قبل از نیوتن کشف شده بود پس نیوتن چه چیزی را و چگونه کشف کرد و به معرفت بشر افزود . چه مسائلی الهام بخش نیوتن شد؟ و…در این بخش به طور مختصر به این سوال پاسخ می دهیم . ولی برای توضیحات کاملتر به مقاله “ نیوتن و گرانش “ مراجعه کنید .

۱) قبل از نیوتن چه چیزی هائی در این ارتباط کشف شده بود ؟

تا زمان نیوتن بسیاری از مسائل در ارتباط با اندازه زمین(شعاع زمین) وحرکات زمین(حرکت وضعی و انتقالی) و حرکات کرات آسمانی (نظریه خورشید مرکزی کپرنیک و قوانین کپلر و…) و همچنین مفهوم نیرو و … شناخته و حل شده بود .کروی بودن زمین هم در همان زمان ارسطو و بطلمیوس مورد قبول واقع شد نیروی جاذبه زمین را هم همه می دانستند و حتی گفتند زمین مانند یک آهن ربای بزرگ همه چیز را به سمت خود می کشد.
نکته : آنچه قبل از نیوتن نمی دانستند این بود که نه تنها زمین بلکه همه اجسام ( از اجسام غول پیکر فضائی گرفته تا اجسام معمولی و حتی اتم ها و… ) نیروی جاذبه دارند .
ما در مقاله های “تاریخچه گرانش “ و“ زندگینامه نیوتن “در مورد آن توضیح دادیم و اینک خلاصه مطالب:
۱-۱)کروی بودن زمین:قدما تصور می کردند زمین مسطح می باشد ولی خیلی زود دلائل کروی بودن زمین توسط دانشمندانی مانند فیلولائوس و ارسطو(قرن چهارم قبل از میلاد)و… کشف شدو بطلمیوس هم درنظریه زمین مرکزی خود این موضوع را پذیرفت (برای مطالعه بیشتر به مقاله “ تاریخچه زمین کروی “ مراجعه کنید)
۲-۱) اندازه گیری شعاع زمین : آریستاخوس در قرن سوم قبل ازمیلادشعاع زمین را اندازه گرفت و ابوریحان بیرونی هم با روش دقیقتری این کار را انجام داد (مقاله “روش های اندازه گیری شعاع زمین “)
۳-۱) اندازه گیری فاصله ماه تا زمین : اولین کسی که فاصله ماه تا زمین را اندازه گیری کرد آریستاخوس بود ( قرن سوم قبل از میلاد ) او فاصله ماه تا زمین را از روی زمان های خسوف بدست آورد . آریستاخوس فاصله ماه تا زمین را ۶۰برابر شعاع زمین تعیین کرد و همانطور که خواهیم گفت منبعی شدبرای این که نیوتن قانون جاذبه خود را فرمول بندی کند( مقاله “خسوف (ماه گرفتگی) “ بخش نهم -اندازه گیری همزمان فاصله ماه تا زمین و قطر ماه با استفاده از روش آریستاخوس )
۴-۱) خورشید مرکزی : کپرنیک به اندیشه های زمین مرکزی پایان داد و نشان داد همه سیاره ها دور خورشید می چرخند ( مقاله “تاریخچه گرانش “ بخش دوم –  نیکلا کپرنیک و آغاز انقلاب علمی )
۵-۱) خدمات گالیله : گالیله سنگ بنای علوم تجربی را پایه گزاری کرد و نشان داد که روش تجربی بهترین روش در پیشبرد علوم می باشد ( مقاله “تاریخچه گرانش “ بخش سوم- گالیله پدر فیزیک نوین)
۶-۱) تیکو براهه : تیکو براهه بزرگترین رصد گری بود که دنیا تا آن روز دیده بود او سیارات را آنطور که از زمین دیده می شوند دید و تمام اطلاعات را ثبت کرد.رصدهای تیکو براهه و جداول او بعدها منبع بسیار با ارزشی شد برای دانشمندان بزرگی همچون کپلر و نیوتن و…(مقاله “تاریخچه گرانش “ بخش چهارم- کپلر و تیکوبراهه)
۷-۱) کپلر : کپلر دستیار تیکو براهه شد و توانست بعد از مرگ تیکوبراهه جانشین او شده و به جداول نجومی و یادداشت های ارزنده تیکو براهه دسترسی داشته باشد و نه تنها بر اساس آنها قوانین خود (قوانین سه گانه کپلر ) را منتشر کرد بلکه این اطلاعات را در اختیار دانشمندان بعد از خود نیز قرار داد (مقاله“تاریخچه گرانش “ بخش چهارم- کپلر و تیکوبراهه)
۸-۱) نیروی گریز از مرکز : نیروی گریز از مرکز به وسیله وسیله فیزیکدان هلندی کریستین هویگنس در سال ۱۶۵۹ کشف شد و فرمول بندی شد .
همچنین دانشمندان دیگری که اطلاعات آنها به نیوتن در جمع بندی و فرمول بندی قانون جاذبه کمک کرد .

۲) ماجرای درخت سیب نیوتن

داستان درخت سیب نیوتن یکی از ماجراهای جالب در علم می باشد با آن که در درستی این داستان شک و شبهه وجود دارد ولی چون این مسئله راهی به سوی درک ساختار گرانش بازکرد و به احترام نیوتن این داستان جدی گرفته شده و حتی درخت سیب هم مشخص شده و به یک مرکز گردشگری تبدیل شده است .
این داستان به قلم ویلیام استاکلی (دوست و نویسنده کتاب های نیوتن ) به این طریق نقل شده است که :
« روزی نیوتن در باغ مادری خود نشسته بود ناگهان سیبی از درخت افتاده و به سر او برخورد می کند . واقعهٔ مذکور این سؤال را به ذهن نیوتن آورد که چرا سیب همیشه مستقیماً به پایین می‌افتد؟ چرا به جای حرکت به سمت مرکز زمین به طرفین یا رو به بالا نمی‌رود؟»  
بعد او این مسئله را به سقوط اجسام بر روی زمین و حرکت ماه بدور زمین و حرکت سیاره ها به دور خورشید و… تعمیم داد و نتیجه گرفت نیروئی به نام جاذبه بین همه اجسام وجود دارد که همه این پدیده ها را به کمک آن می توان توجیه کرد ولی تا تئوریزه کردن و فرمول بندی این قانون هنوز راه زیادی مانده بود . 

۳) ماجرای بازی بچه ها و نیروی گریز از مرکز

حال مسئله نیروئی که سیارات را در اطراف خورشید نگه می دارد و باعث سقوط اجسام در روی زمین می شود کشف شده بود (هر چند هنوز فرمول بندی نشده بود) ولی هنوز یک مسئله مانده بود .
حال نیوتن در این اندیشه بود که خب اگر نیروی جاذبه سیارات را به طرف خورشید جذب می کند و ماه را در اطراف زمین نگه داشته چرا سیارات روی خورشید سقوط نمی کنند؟
در سال ۱۶۶۷نیوتن بخاطر آورد که وقتی در مدرسه درس می خوانده بچه ها سطل آبی را که یک طناب به دسته آن بسته شده بود در هوا چرخانده و کسی که با سرعت مناسب بتواند سطل را بچرخاند و آبی از درون سطل به بیرون نریزد برنده بازی می باشد.چرا آب درون سطل ،از سطل بیرون نمی ریزد؟ چه عاملی جلو ریختن آب را می گیرد؟ ناگهان فکری به ذهن نیوتن می رسد و پاسخ سوال خود را پیدا می کند. نیروی گریز از مرکز

۴) ماه و نیروی گرانش

تا این جای کار مشخص شده بود که بین هر دو جسم نیروی جاذبه وجود دارد که با افزایش جرم زیاد و با با افزایش فاصله کم می شود . ولی چگونه و با چه نسبتی؟در اینجا در مورد آن توضیح می دهیم توضیحات بیشتر و فرمول بندی تا رسیدن به فرمول اصلی قانون جاذبه عمومی در مقاله “ نیوتن و گرانش “ به طور کامل تشریع شده است . این موضوع که نیروی جاذبه نسبت مستقیم با جرم دو جسم دارد مسئله ساده تری بود ولی مسئله مهم دیگر نسبت نیروی جاذبه با فاصله بود .
نیوتن برای پیدا کردن ارتباط نیروی جاذبه با فاصله پیش خودش حساب کرد که نیروی جاذبه در یک جسم کروی به گونه ای عمل می کند که انگار تمام جرم جسم (زمین) درمرکز آن جمع شده است.سیب که از درخت سقوط می کندفاصله اش تا مرکز زمین برابر شعاع زمین است ولی فاصله ماه تا مرکز زمین ۶۰ برابر شعاع زمین می باشد . نیوتن شتاب جاذبه ای(مقدار g) که ماه را به سمت زمین جذب می کند (که متناسب با نیروی جاذبه زمین روی ماه می باشد) حساب کرد (نیروی جاذبه را با نیروی گریز از مرکزی که بر اثر گردش ماه به دور زمین ایجاد می شود برابر گرفت ) و نتیجه گرفت نیروی جاذبه ای که ماه را در مدارش نگه می دارد ۳۶۰۰برابر کمتر از موقعی است که ماه همانند سیب در سطح زمین قرار داشت بنابراین نیرو متناسب با عکس مجذور فاصله می باشد ( ۳۶۰۰= ۶۰^۲ ) که ما جزئیات این محاسبه را در مقاله “ نیوتن و گرانش” شرح دادیم .

۳- قانون جاذبه عمومی نیوتن و اثرات آن

در این بخش در مورد قانون جاذبه عمومی و نتایج آن توضیح می دهیم . همان قانون معروفی که نیوتن سرانجام توانست آن را فرمول بندی کرده و به صورت فرمول ریاضی اعلام کند . آنچه نیوتن ارائه کرده به صورت برداری و دیفرانسیلی می باشد و ما برای سادگی کار در این بخش و مقاله های دیگر فقط شکل ساده شده آن را نوشته و هر کجا نیاز شد از معادله های اصلی استفاده می کنیم .

۱) قانون جاذبه عمومی نیوتن

قانون گرانش جهانی یا قانون جاذبه عمومی نیوتن به این شکل بیان می شود :
«بین هر دو جسم نیروی جاذبه ای وجود دارد که نسبت مستقیم با جرم آن دو جسم داشته و نسبت عکس با مجذور فاصله دارد »

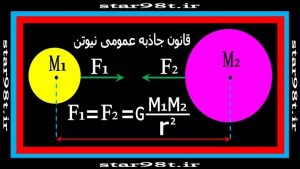
شکل شماره ۱ – قانون جاذبه عمومی نیوتن

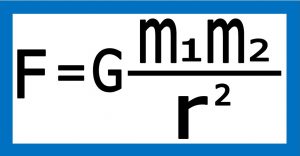
۲) حالت های دیگر قانون جاذبه عمومی نیوتن

باید توجه داشت آنچه به عنوان فرمول گرانش استفاده می کنیم در واقع حالت ساده شده این فرمول است برای حل تمام مسائل مربوط به گرانش ( ازجمله بدست آوردن مدارهای سیارات و اثبات قوانین کپلر ) لازم است حالت کلی آن را که به صورت دیفرانسیلی یا برداری می باشد بنویسیم . ابتدا مسئله را ساده تر کنیم و حالت برداری فرمول را بنویسیم .

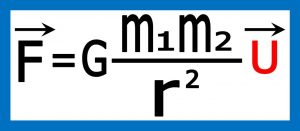
نیرو یک کمیت برداری می باشد و بنابراین نتیجه هم باید بردار باشد ولی کمیت های m₁،m₂،G،r هیچکدام بردارنیستند از این رو یک بردار یکه (بردار یکه برداری است که اندازه آن برابر یک است و هیچ واحدی هم ندارد بنابراین تعغیری در نتیجه نمی دهد ) اضافه کردیم. جهت بردار یکه “U”هرچه باشد جهت بردار F هم همان است .فرم دیفرانسیلی معادله به این صورت است .

نکته : بخاطر جلوگیری از پیچیدگی مطلب در بقیه مطالب این مقاله سعی می شود حتی الامکان معادله گرانش را به همان شکل ساده آن بکار ببریم .

۳) نیروی گرانش به عنوان دو نیروی عمل و عکس العمل

طبق قانون سوم نیوتن نیروها به صورت جفت نیروی عمل و عکس العمل وارد می شوند که به دو جسم M₁ و M₂ وارد می شوند . بنابر این وقتی سیب به زمین سقوط می کندگرانش زمین به سیب نیروی F₁ را وارد می کند . سیب هم نیروی گرانش F₂ را به زمین وارد می کند و این دو نیرو برابر و در جهت مخالف هم هستند یعنی داریم  F₁=-F₂ ( علامت منفی نشان می دهد که جهت دو نیرو خلاف یکدیگر هستند) سیب بر اثر نیروی F₁ طبق قانون دوم نیوتن (F=ma) در جهت نیرو (مرکز زمین) شتاب می گیرد که مقدار این شتاب برابر همان شتاب جاذبه “g” می باشد به کل کره زمین نیز همان نیرو وارد می شود و زمین نیز در جهت مخالف سیب شتاب می گیرد ولی زمین بخاطر این که بسیار بسیار … بزرگتر از سیب می باشد شتاب بسیار بسیار … کوچکی می گیرد که با پیشرفته ترین دستگاه ها هم قابل تشخیص نیست.(شکل شماره ۲ )

شکل شماره  ۲ – سیب و زمین همدیگر را با نیروی یکسان جذب می کنند

۴) گرانش چه مسائلی را توصیف می کند . 

گرانش همواره به صورت جاذبه بوده و بر تمام اجرام جرم دار تاثیر می کند و به کمک این قانون می توان سقوط اجسام در مجاورت زمین ، حرکت ماهواره ها در مدار زمین ، گردش سیاره ها بر گرد خورشید ، گردش قمرها بر گرد سیارات و… را توجیه کرد.(تنها در حوزه هائی که نسبیت عام و کوانتم وارد عمل می شود نمی توان از قانون گرانش استفاده کرد ) همچنین گرانش توضیح می دهد که اگر یک پرتابه را در روی یک سیاره به طرف بالا پرتاب کنیم مسیری منحنی را طی خواهد کرد.(مسیری به شکل سهمی) و اگر سرعت پرتابه به اندازه کافی زیاد باشد می تواند در مدار سیاره قرار گرفته و یا حتی از حوزه جاذبه سیاره فرار کند .
همچنین در هنگام تشکیل کهکشان ها و ستارگان این نیروی گرانش است که ابرهای گازی را فشرده کرده و موجب تشکیل ستارگان و … می شود در مورد سیارات این نیروی گرانش است که ذرات گرد و غبار را بدور خود جمع کرده و ذرات بزرگتر و بزرگتر و… تشکیل داده و سرانجام منجر به شکل گیری سیارات می شود . ( در این مورد در فصل ها و مقاله های آینده به طور کامل توضیح می دهیم) بدون شناخت کافی گرانش بسیاری از مسائل در نجوم و اختر فیزیک و … بدون جواب می ماند.همچنین در زمین شناسی برای شناسائی معادن و یا برسی فعالیت های آتش فشانی ازتاثیرجاذبه استفاده می کنند.
در مورد کاربردهای گرانش در مکانیک کلاسیک و نجوم و … علوم مختلف در مقاله های دیگر فصل “جمع بندی مقاله های فصل هفتم – گرانش(۱)“ و همچنین فصل های “جمع بندی مقاله های فصل هشتم– گرانش(۲)“ و “جمع بندی مقاله های فصل نهم – گرانش(۳)   “ توضیحات کافی دادیم .

۵) گرانش به عنوان یکی از چهار نیروی اصلی طبیعت

کلیه نیروهای طبیعت را می توان در چهار نیرو خلاصه کرد . این چهار نیرو را “نیروهای بنیادی  طبیعت” می نامند. یک نیرو موقعی بنیادی نامیده می شود که نتوان آن را با نیروهای دیگر توصیف کرد .این چهار نیرو عبارتند از : « نیروی هسته‌ای ضعیف، نیروی هسته‌ای قوی، نیروی الکترومغناطیسی و گرانش »  که ماهیت همه نیروها بجز گرانش کاملا مشخص شده است . در این مورد در مقاله های “” رازهای گرانش “ و “ گرانش و نسبیت عام“بیشتر توضیح می دهیم .

 

۶) جرم لختی ، جرم گرانشی و خاصیت هم ارزی

طبق قانون اول نیوتن اگر به جسمی نیرو وارد نشود جسم حالت سکون و یا حرکت مستقیم الخط خود را حفظ می کند ولی برای تعغیر وضعیت حرکتی جسم طبق قانون دوم نیوتن باید نیرو مصرف شود که این نیرو متناسب با جرم حسم می باشد و فیزیکدان ها آن را خاصیتی ازجرم می دانند که به آن “جرم لختی” می گویند .
همچنین نیروی گرانش نسبت مستقیم با جرم دارد  و این جرم میزان نیروی وارده را نشان می دهد که به آن “جرم گرانشی” می گویند . می توان ثابت کرد که جرم گرانشی و جرم لختی برابرند که این برابری را ” اصل هم ارزی ” می نامند .  

۴- جاذبه حاصل از یک جسم عظیم و اثرات آن 

اگر چه همه اجسام مادی چه بزرگ و چه کوچک بر همدیگر نیروی گرانش وارد می کنند که توسط فرمول گرانش جهانی اعمال می شود ولی باید بدانیم که گرانش در بین چهار نیروی بنیادی نیروی بسیار کوچکی می باشد به طوری که گرانش بین اجسام بسیار کوچک (اتم ها و مولکول ها و… )که هیچ حتی بین اجسام معمولی ( مانند دو انسان یا حتی دو کشتی غول پیکر و…) هم قابل مشاهده و احساس نیست (اگر چه تا حدودی قابل اندازه گیری هست) تنها بین اجسام بزرگ سماوی (ستارگان و سیارات و قمرها و… ) است که این نیرو خود را نشان می دهد . پس عمده کاربرد گرانش نیروی جاذبه کره زمین و نیروهائی است که بین ستارگان و سیارات و بین قمرها و سیارات و… وجود دارد . پس آنچه ما در این بخش بررسی می کنیم همین موضوعات است.بنابراین ابتدا نیروی وارد شده از طرف یک جسم کروی را بررسی می کنیم (زیرا اجرام آسمانی بیشتر کروی هستند)

۱) قضیه پوسته ( نیروی وارد شده از طرف پوسته کروی )

برای بررسی نیروی وارد شده از طرف یک جسم کروی ابتدا نیروی وارد شده از طرف یک پوسته کروی (پوسته کروی عموما به کره توخالی که ضخامت آن در مقایسه با کره ناچیز می باشد ) را بررسی می کنیم . دو قضیه در این ارتباط وجود دارد که به ” قضیه های پوسته ” ( قضیه مطلبی است که باید اثبات شود) مشهور هستند .
دو حالت در نظر می گیریم . حالت اول این است که جسم در بیرون از پوسته کروی قرار دارد (شکل شماره ۳) و حالت بعدی این است که جسم در داخل پوسته کروی قرار دارد . می خواهیم بررسی کنیم ببینیم نیروی گرانش وارد شده بر جسم چقدر است؟
۱-۵) قضیه پوسته یک : نیروی وارد شده از طرف یک پوسته کروی به جسمی که در بیرون از پوسته قرار گرفته باشد به گونه ای است که انگار تمام جرم پوسته در مرکز آن متمرکز شده باشد .
۲-۵) قضیه پوسته دو : نیروی وارد شده از طرف یک پوسته کروی به جسمی که در داخل پوسته قرار گرفته باشد صفر است یعنی هیچ نیروی گرانشی به جرم داخل پوسته وارد نمی شود .
بنابراین اگر در دورن زمین چاهی حفر کرده و شخصی ته جاه باشدتنها آن بخش از کره زمین که زیر پای شخص می باشد بر او نیروی گرانش وارد می کند . و قسمتی که بالای سر او باشد نیروی گرانشی وارد نمی کند .
اثبات این قضیه از طریق فرم دیفرانسیلی فرمول گرانش امکان پذیر می باشد و بعلت پیچیدگی آن در اینجا اثبات نمی شود .(علاقمندان می توانند : به کتاب فیزیک هالیدی “جلد اول بخش ۱۶-گرانش  “ صفحه ۴۰۰مراجعه کنند )

۲) نیروی وارد شده از طرف یک جسم کروی

یک کره کامل را می توان مجموعه ای از بیشمار پوسته های کروی تو در تو با ضخامت بسیار ناچیز تصور کرد و از طریق دیفرانسیل و انتگرال گیری ثابت کرد قصیه پوسته در مورد کره کامل هم صدق می کند.
در مورد کره کامل و توپر باز هم برای جسم خارج از کره مرکز اثر گرانش را باید مرکز کره در نظر گرفت این مسئله بسیار مهم است از این رو که در روی زمین و سیارات و…نیروی گرانش سطحی که موجب وزن اشیا می شودبه این مسئله وابسته است که باید فاصله را تا مرکز ستاره و سیاره و…حساب کنیم. همچنین درمحاسبه نیروی جاذبه بین دو جسم کروی ( سیاره و ستاره و…) مرکز کره ها را باید ملاک قراردهیم.
حال در مورد پوسته کروی که جسم داخل پوسته قرار داشته باشد فرقی نمی کند که پوسته توخالی یا توپر باشد بلکه اگر جسمی درون یک کره (مثلا داخل چاهی در داخل زمین)قرار داشته باشد تنها آن بخش از کره که در زیر پای جسم(یا ناظر) قرار داشته باشد نیروی گرانش ایجاد می کند و آن بخش از کره که در بالای سر جسم قرار داشته باشد در تولید نیروی جاذبه هیچ نقشی ندارد .
در مقاله “ گرانش سطحی ” در بررسی رابطه گرانش با عمق و همینطور در مقاله “چاه بی انتها ”  در ارتباط با دوره تناوب و سرعت جسمی که درون چاه سقوط می کند همین مسئله را مورد بررسی قرار می دهیم .

شکل شماره ۳ – قضیه پوسته یک و دو

۳) تعمیم قضیه پوسته به اجسام غیر کروی

حال اگر منبع اصلی گرانش (جسم مرکزی )کروی نباشدگرانش برای جسمی که درون و بیرون منبع گرانش قرار دارد چگونه است؟ این سوال چندان هم بی ربط نیست اگر چه اجسام بزرگ (ستاره ها و سیاره ها و…) با تقریب بسیار خوبی کروی هستند ولی سیارک های غول آسائی وجود دارند که ده ها و صدها کیلومتر طول داشته و گرانش در خور توجهی ایجاد می کنند و بهیچ عنوان هم کروی نیستند و شکل کشیده ای دارند ( شکل شماره ۴) قضیه پوسته را می توان به اجسام غیر کروی به این صورت تعمیم داد :
۱-۳) برای جسمی خارج از منبع گرانش : نیروی وارد شده از طرف جسم بزرگ مرکزی برجسمی خارج از آن به گونه ای است که انگار تمام جرم جسم در “مرکز جرم “ متمرکز شده است . تعریف مرکز جرم در مقاله “مرکز جرم “  توضیح داده می شود . درواقع مرکز جرم کره هم مرکزکره می باشد پس حالت کره کامل در واقع حالت خاصی از قضیه می باشد.
۲-۳) برای جسمی در داخل منبع گرانش : دقیقا مانند کره است یعنی آن قسمتی از منبع گرانش که جسم ما را احاطه کرده است هیچ گرانشی ایجاد نمی کند و تنها آن قسمتی از منبع گرانش نیرو ایجاد می کند که جسم ما در بیرون از آن قرار دارد . و البته فاصله هم تا مرکزجرم قسمت داخلی حساب می شود . ( شکل شماره  ۵ ) 
نکته ۱ : البته نیروی جاذبه با اجسام بزرگ (ستارگان و سیارات و…) محدود نمی شود و قضیه پوسته در مورد همه اجسام (ریز و درشت و.. ) صادق است آنچه باعث می شود فقط پای اجسام بزرگ را پیش بکشیم ناچیز بودن نیروی گرانش برای اجسام خرد و ریز است .
نکته ۲ : در سیستم هائی متشکل از دو یا چند جسم باز هم مرکز گرانش مرکز جسم اجسام است. در مقاله “مکانیک مداری و قوانین کپلر(۲) “ این مسئله را به طور کامل شرح می دهیم .

شکل شماره ۴ – یک سیارک بی نظم

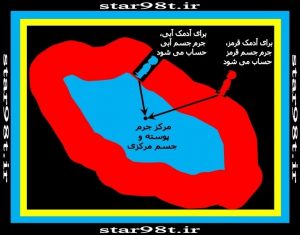
شکل شماره ۵ – قضیه پوسته برای شکل غیر کروی

۴) میدان گرانشی

یک جسم بزرگ مرکزی (مانند کره زمین) را در نظر بگیرید که به اجسام کوچک پیرامون خود نیرو وارد می کند مقدار نیروی وارد شده بر حسب فاصله تا مرکز جرم (مرکز زمین) تعغیر می کند( هرچه فاصله بیشتر شود نیرو نیز کمتر می شود )برای بررسی مقدار نیرو در اطراف منبع جاذبه  ازتعریف میدان گرانشی استفاده می کنیم .
به صورت خیلی ساده میدان گرانشی (Gravitational field) فضائی در اطراف یک جسم سنگین می باشد که در آن فضا نیروی گرانشی به اجسام پیرامون آن وارد می شود.اصولا میدان اختصاص به نیروی گرانش ندارد و در مورد سه نیروی بنیادی دیگر (نیروی هسته‌ای ضعیف، نیروی هسته‌ای قوی،نیروی الکترومغناطیسی ) هم میدان تعریف می شود . پس عموما میدان مجموعه نقاطی است که در آن نقاط نیرو اعمال می شود .
نکته ۱: باید توجه کرد تعریفی که از میدان و گرانش ارائه شد در مکانیک کلاسیک معتبر است و در نسبیت عام و مکانیک کوانتمی تعریف میدان تعغیر می کند .
نکته ۲ : میدان گرانشی فقط در مورد اجرام عظیم نیست در واقع هر جسم بسیار کوچک هم در اطراف خود میدان گرانشی کوچکی دارد ولی در اینجا ما اجسام بزرگ و عظیم رادر مقابل اجسام کوچک بررسی می کنیم.

۵) شتاب گرانشی چیست ؟

نیروی گرانش در اطراف یک جسم سنگین (مانند زمین) همه اشیا را به سمت خود می کشد و طبق قانون دوم نیوتن این نیرو شتاب ایجاد می کند و این شتاب برای تمام اجسامی که درنزدیکی زمین (و یاهر سیاره یا…دیگر ) قراردارند کمابیش یکسان است و همانطور که ثابت می شود به جرم جسم بستگی ندارد. (توضیح بیشتر در این مورد را در مقاله “جاذبه زمین”می دهیم) این شتاب را شتاب گرانش سطحی می گویند. و با “g”نشان می دهندمقدار آن درمجاورت سطح زمین حدود ۹/۸می باشد. (توضیحات کاملتر در موردشتاب گرانشی و روش های بدست آوردن آن در مقاله های“ شتاب گرانشی زمین ” و “ ثقل سنجی “ می دهیم)

۶) انرژی پتانسیل و جنبشی

به صورت خیلی خلاصه انرژی قابلیت انجام کار می باشد. و کار هم حاصل ضرب نیرو در جابجائی می باشد ( در مورد مفاهیم کار و انرژی در مقاله “ کار و انرژی “ توضیح کافی می دهیم ) انرژی انواع مختلف دارد مانند (انرژی شیمیائی ، انرژی هسته ای ، انرژی الکتریکی و… ) ولی همه انرژی ها در کل به دو صورت انرژی پتانسیل و انرژی جنبشی تقسیم می شوند . انرژی جنبشی انرژی است که بخاطر حرکت یک جسم ایجاد می شود و انرژی پتانسیل انرژی است که در یک جسم نهفته می باشد مانند : انرژی نهفته در باطری ، انرژی شیمیائی ، انرژی هسته ای و… انرژی پتانسیل گرانشی

۷) انرژی پتانسیل گرانشی

یکی از انواع انرژی پتانسیل ،انرژی پتانسیل گرانشی می باشد . وقتی دو جسم با هم در تماس باشند نیروی گرانش نمی تواند موجب شتاب آنها شود ولی وقتی از هم دور می شوند و بعد رها می شوند به طرف هم حرکت کرده و هر لحظه به سرعت آنها اضافه می شود این یعنی انرژی جنبشی بدست می آورند بنابر قانون بقای انرژی ، انرژی نمی تواند از هیچ بوجود آید پس انرژی جنبشی بوجود آمده بعلت وضع دو جسم جرم دار نسبت به هم بوجود آمده و در آنها ذخیره شده است . این انرژی نهفته را انرژی پتانسیل گرانشی می گویند. در مقاله ”  گرانش و انرژی ” در این باره توضیح مفصل می دهیم .
همچنین توضیح می دهیم که چگونه یک جسم عظیم مرکزی (مانند کره زمین) در نظرگرفته و انرژی پتانسیل را نسبت یه سطح زمین می سنجیم .

۵- آزمایش کاوندیش

نیوتن قانون جاذبه عمومی را کشف کرد و توانست بسیاری از پدیده های خلقت را در رابطه با حرکت اجرام سماوی و… توجیه کند و همچنین قوانین کپلر و یکسری پدیده های دیگر را در فیزیک و مکانیک و نجوم را توانست با قانون جاذبه عمومی توجیه کند و برای خود شهرت جهانی کسب کند .
ولی هنوز یک کار دیگر مانده بود برای استفاده از فرمول های قانون گرانش جهانی و حل آنها نیاز به اندازه گیری ثابت “G” ( ثابت جاذبه ) بود کاری که در زمان نیوتن امکان آن وجود نداشت ولی کمتر از ۶۰ سال بعد این ثابت هم اندازه گیری شد در این بخش در مورد اندازه گیری “ثابت جهانی گرانش” و نتایج آن توضیح خواهیم داد .

۱) اهمیت ثابت های بنیادی در فیزیک

ثابت های فیزیکی یکی از مهمترین فاکتورها برای محاسبات فیزیکی و توجیه قوانین طبیعت می باشند . چندین ثابت فیزیکی وجود دارد که به عنوان مثال می توان به : سرعت نور c ، بار سکون الکترون  e ، جرم سکون پروتون m_p، ثابت پلانک h و… ثابت گرانشی G اشاره کرد . برای محاسبات فیزیکی مقادیر عددی این ثابت ها باید با دقت بسیار زیاد بدست بیاید این کار بسیار سخت بوده و هست و دانشمندان در طی صدها سال با روش های بسیار دقیق توانستند این مقادیر را بدست بیاورند و در دوران ما مرتب این ثابت ها با پیشرفته ترین دستگاه ها اندازه گیری تا مقادیر هرچه دقیق تری بدست بیاید . ولی در این میان چندین سوال پیش می آید . آیا واقعا این اعداد ثابت هستند و در طول زمان تعغیری نمی کنند؟ آیا مقدار آنها در همه جای جهان همین مقدار است؟
پاسخ مثبت است نه تنها این اعداد ثابت هستند بلکه در همه جای جهان ما همین مقدار هستند .
نکته بسیار جالب این است که از همان ابتدای پیدایش جهان با بیگ بنگ (در مورد بیگ بنگ و خلقت جهان در آینده توضیحات بیشتری می دهیم ) این ثابت ها همین مقداری که امروز بودند بوجود آمدند و اگر یکی از آنها اندکی کمتر و یا بیشتر بود جهان ما (کهکشان ها و ستارگان و… خود ما) بوجود نمی آمد.خداشناسان این امر را دلیلی بر وجود خالق یکتا (خداوند) می دانند که ناظر برهمه چیز است. این نظریه را “نظریه جهان نظیم‌شده “ می دانند . در این مورد در آینده توضیح خواهیم داد .

۲) اندازه گیری نِویل مسکلین

نِویل مسکلین (Nevil Maskelyne)ستاره شناس و فیزیکدان انگلیسی متولد ۱۷۳۲ در لندن بود . او پنجمین منجم بزرگ سلطنتی و عضو انجمن سلطنتی بریتانیا بود . یکی از مهمترین کارهای او اندازه گیری ثابت گرانشی بود . او یک کوه  به نام “ شیهالیون “ ( کوهی در اسکاتلند ) پیدا کرد که مخروطی بسیار منظم بود و براحتی از روش های مختلف توانست ارتفاع و ابعاد و در نتیجه حجم کوه را اندازه گیری کند . و بعد سنگ هائی از کوه را گرفته و چگالی آنها را حساب کرده و با استفاده از چگالی جرم متوسط کوه را محاسبه کرد در مرحله بعد به کنار کوه رفت و با استفاده از یک شاغول توانست میزان انحراف گلوله سربی شاغول را از خط عمود اندازه گیری کرده (مقداری که بدست آمد حدود ۱۱ ثانیه قوسی بود) بنابراین نیروی گرانشی بین شاغول و کوه را حساب کرد و به این وسیله توانست مقدار ثابت گرانش “G” را حساب کند. او توانست برای ثابت جهانی گرانش و همچنین جرم حجمی زمین  (ρe ) این مقادیر را بدست بیاورد :

G=8.3*10^-11 m³/Kg.S²  —- ρe=4400 Kg/m³

که البته مقدار خیلی دقیقی نبود ولی در نوع خود یک شاهکار به حساب می آمد .

۳) جان میشل و  تلاش های او

جان میشل (متولد۲۵ دسامبر ۱۷۲۴)ستاره شناس و زمین شناس انگلیسی بود . در واقع روش درست اندازه گیری ثابت گرانش را او ابداع کرد.جان میشل برای اندازه گیری ثابت گرانش در سال ۱۷۸۳یک ترازوی پیچشی (ترازوی پیچشی ترازوئی است که نیروی وارد شده را که سبب پیچ خوردن یک ریسمان می شود اندازه گیری می کند) بسیار دقیق ساخته بود ( البته کولن اولین کسی بود که ترازوی پیچشی را اختراع کرد ولی جان میشل به منظور اندازه گیری دقیق ثابت گرانش ترازوی دقیقتری ساخت) ولی قبل از تکمیل و استفاده از این وسیله در سال ۱۷۹۳ از دنیا رفت و نتوانست کارش را تکمیل کند دو دانشمند به نام های “ فرانسیس جان هاید “ و “ هنری کاوندیش “ که از دوستان و همکاران میشل بودند روی پروژه میشل کار کرده و آن را تکمیل کردند . در قسمت بعد شرح خواهیم داد که چگونه هنری کاوندیش توانست ثابت جهانی گرانش را اندازه گیری کند ولی قبل از آن نگاهی بیندازیم به زندگانی هنری کاوندیش دانشمندی که با اندازه گیری ثابت گرانش توانست برای خودش افتخار جهانی کسب کند .

۴) هنری کاوندیش Henry Cavendish

سر هنری کاوندیش(Henry Cavendish) در۱۰ اکتبر ۱۷۳۱در شهر نیس ساردنی (ساردنی در آن زمان کشور مستقلی بود ولی هم اینک جزء ایتالیا است) بدنیا آمد. پدرش یک دانشمند ثروتمند و عاشق علوم و تحقیقات بود او به لندن آمد و جزء انجمن سلطنتی شد . هنری در بهترین مدارس لندن درس خواند و در ۱۸سالگی ( در ۲۴ نوامبر ۱۷۴۸) وارد دانشگاه کمبریج (کالج سنت)د ولی سه سال بعد بدون دریافت هیچگونه مدرکی انصراف داد و بیرون آمد. او آزمایشگاه مجلل خود را داشت و در آن با پدرش آزمایشات مختلف انجام می داد . آزمایش هائی در فیزیک و شیمی و … که منجر به کشفیات زیادی شد(کشف هیدروژن ، قانون بقای انرژی و… بدست آوردن ثابت گرانش ) که اگر چه بیشتر آنها را تا دم مرگ منتشر نکرد ولی بعدا معلوم شد کار هنری کاوندیش بود . هنری بسیار خجالتی بود (بخصوص از خانم ها خجالت می کشید) ولی این مانع نشد که مدارج پیشرفت و ترقی را طی نکند در سال ۱۷۶۰ به عضویت انجمن سلطنتی انتخاب شد او ریاست یک گروه را بر عهده گرفت که به کار هواشناسی می پرداختند همچنین در رصدخانه سلطنتی کار می کرد . هنری به ریاست کمیته ای در انجمن سلطنتی انتخاب شد که کار کمیته بررسی مقاله های ارسال شده به انجمن قبل از چاپ در نشریات معتبر انجمن سلطنتی بود . بعد از مرگ پدرش ثروت عظیمی به او رسید او خانه ای مجلل در جنوب لندن خرید و کتابخانه و آزمایشگاه و… تجهیزات خود را به آنجا منتقل کرد هنری کاموندیش در سال ۱۷۹۸با تکمیل ترازوی پیچشی جان میشل توانست ثابت جهانی گرانش را بدست آورده و برای خود شهرت جهانی کسب کند .(به عبارتی او نخستین کسی شد که توانست زمین را وزن کند ) به پاس این خدمات در سال ۱۸۰۰به ریاست انجمن سلطنتی انتخاب شد و سرانجام در۲۴ فوریه ۱۸۱۰در سن۷۶ سالگی درحالی در گذشت که ثروتمندترین فرد لندن بود .
هم اکنون جاده ای که به خانه قدیمی او می رود به نام او نامگذاری شده است و یک آزمایشگاه در دانشگاه کمبریج هم به افتخار او به نام آزمایشگاه کاوندیش نامگذاری شده است .

 شکل شماره ۶- هنری کاوندیش

۵) آزماش کاوندیش و ترازوی پیچشی

آزمایش کاوندیش ( Cavendish experiment)، آزمایشی است که در سال ۹۸–۱۷۹۷ توسط هنری کاوندیش، دانشمند بریتانیایی انجام شد. این آزمایش نخستین آزمایشی است که در آن نیروی گرانش بین اجسام در آزمایشگاه محاسبه شد،و نیز نخستین آزمایشی است که در آن مقدار دقیقی برای ثابت گرانش و جرم زمین به دست آمد. همانطور که گفته شد جان میشل قبل از کاوندیش یک ترازوی پیچشی بسیار دقیق ساخته بود که مقدار نیروی بسیار کوچکی را که باعث پیچش ریسمان نگهدارنده ترازو می شد اندازه گیری می کرد . بعد از مرگ میشل این ترازو به فرانسیس جان هاید ولاستون و بعد به هنری کاوندیش رسید . کاوندیش برای منظور خود این ترازو را بازسازی کرد و از آن برای تعیین ثابت گرانش بهره برد .

۶) نحوه کار ترازوی پیچشی

کاوندیش با ترازوی ساخته شده توانست نیروی گرانش بین دو گلوله سربی بزرگ و گلوله های کوچک را اندازه گیری کرده و با دانستن وزن گلوله ها ثابت گرانشی “G” را اندازه بگیرد در شکل شماره ۷ نحوه انجام آزمایش نشان داده شده است . ما در اینجا با توجه به شکل شماره ۷نحوه آزمایش و قسمت های مختلف آن را شرح می دهیم.

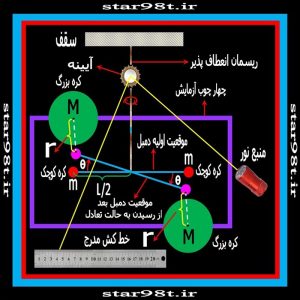
شکل شماره ۷ – ترازوی پیچشی کاوندیش

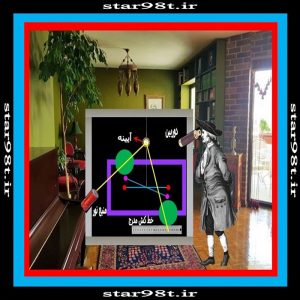
شکل شماره ۸ – ایزوله کردن ترازو

۶-۱) گلوله های بزرگ سربی : ترازوی کاوندیش از دو گلوله سربی بزرگ تشکیل شده که به صورت کاملا افقی به یک چهار چوب ثابت شده و حرکت نمی کند .
۶-۲) گلوله های کوچک  : دو گلوله کوچک به یک میله محکم بسته شده و تشکیل یک دمبل را داده و این دمبل  توسط یک ریسمان نازک انعطاف پذیر به صورت افقی آویخته شده است . ( جرم میله دمبل در مقابل جرم گلوله های دمبل قابل صرف نظر کردن بود )
۶-۳) ریسمان : ریسمان از جنس ماده ای انعطاف پذیر بوده که در مقابل چرخش و پیچیده شدن بسیار کم مقاومت کند . ریسمان هرچه بیشتر پیچیده شود مقدار این مقاومت بیشتر می شود . بنابراین نیروی گرانش گلوله ها به اندازه ای می تواند ریسمان را بپیچاند که با نیروی مقاوت ریسمان در مقابل پیچیده شدن برابری کند . این ریسمان و دمبل های کوچک سربی محکم به سقف بسته شده است .
۶-۴) آینه : نیروی گرانش گلوله ها بسیار ناچیز می باشد بنابراین دمبل چرخش بسیار کمی می تواند داشته باشد و مشاهده این چرخش کوچک به سادگی امکان پذیر نیست بنابراین یک آینه به ریسمان بسته شده که پرتوی را که از یک نقطه ثابت به آن می تابد را روی یک صفحه مدرج بازتاب داده به این ترتیب حرکت چرخشی دمیل (مجموعه گلوله های سربی کوچک و میله بین آنها) چند برابر می شود. و به آسانی روی صفحه مدرج خوانده می شود .
کاوندیش نیک می دانست که این آزمایش بسیار حساس است و هرگونه حرکت هوا و نوسانات دمای هوا می تواند در نتیجه آزماس تاثیر بگذارد بنابراین ترازو و دستگاه را در یک قاب شیشه ای از محیط اتاق جدا کرد و با نصب دوربین خودش از خارج از چهارچوب ترازو به مشاهده و ثبت داده ها پرداخت . ( شکل شماره ۸ ) 

۷) نتیجه محاسبات کاوندیش

کاوندیش مقدار ثابت گرانش را  “ G=6.75*10^-11 “ بدست آورد که بسیار به مقدار واقعی نزدیک بود . و با این کار برای خود شهرت جهانی بدست آورد بعد از بدست آوردن ثابت گرانش امکان این فراهم شد که جرم زمین و همچنین جرم خورشید را محاسبه کند . ( این محاسبات در بخش هفتم “ محاسبه جرم خورشید و زمین “ انجام شده است) و با توجه به حجم زمین جرم حجمی زمین را نیز توانست بدست بیاورد . بنابراین گفته اند کاوندیش نخستین کسی بود که به معنای واقعی زمین را وزن کرد .
همچنین امکان این نیز پیش آمد که با توجه به قانون سوم کپلر جرم همه سیاره ها را هم بدست بیاورند . امروزه با ارسال ماهواره به گرد قمرها و سیاره ها و هر جرم در منظومه شمسی که ارسال کاوشگر به آن امکان داشته باشد می توانند جرم همه اجرام منظومه شمسی را محاسبه کنند .

۸) اندازه گیری پوئین و تینگ

در قرن ۱۹ دو دانشمند به نام های پوئین و تینگ اصلاحات مهمی در آزمایش کاوندیش انجام دادند و توانستند مقدار دقیقتری برای ثابت گرانش بدست بیاورند .

۹) مشکل اندازه گیری ثابت G

گرانش ضعیف ترین نیروی شناخته شده در بین نیروهای بنیادی می باشد با توجه به کوچک بودن ثابت گرانش اندازه گیری آن بسیار مشکل است . با آن که تعداد بسیار زیادی از دانشمندان از زمان کاوندیش تا امروز سعی کردند به طرق مختلف این ثابت را بدست بیاورند هنوز نتوانستند با دقتی که ثابت های دیگر فیزیکی را اندازه گیری می کنند این ثابت فیزیکی را اندازه گیری کنند . نتایج نشان می دهد که خطای اندازه گیری ثابت G حدود ۲۰ برابر بیشتر از اندازه گیری ثابت های دیگر فیزیکی است. همین ترازوی پیچشی با افت و خیزهای دما و… می تواند خطاهای بزرگی در نتیجه آزمایش ایجاد کند .

۱۰) آزمایش تعیین G در قرن ۲۱

آزمایش های تعیین مقدار G ادامه پیدا کرد در طول قرن بیستم و ۲۱ افراد مختلفی این آزمایش را انجام داده و نتایج متفاوتی برای مقدار G بدست آوردند در تازه ترین آزمایش ها که سال ۲۰۱۱ انجام شد :
دانشمندی به نام تری کوئین (Terry Quinn) و همکارانش در دفتر بین‌المللی وزن‌ها و اندازه‌گیری‌ها در فرانسه دستگاه بسیار پیشرفته تری (نوعی ترازوی پیچشی)ساختند و دست به اندازه گیری مقدار G زدند تا بلکه مقدار دقیق آن را بهبود ببخشندجدیدترین نتیجه ای که بدست آوردند : G=6.67545*10^-11 “ می باشد.

شکل شماره  ۹ – دستگاه تری کوئین و همکارانش برای تعیین مقدار G

۶- محاسبه ثابت گرانش

در بخش قبل در مورد کاوندیش و ترازوی او و این که چگونه به کمک این ترازو توانست ثابت گرانشی را بدست بیاورد و تلاش های بعد از او پرداختیم در این بخش محاسبات انجام شده توسط کاوندش را کامل توضیح می دهیم این بخش به درد کسانی می خورد که به محاسبات ریاضی علاقه داشته و حداقل در سطح دیپلم متوسطه ریاضی فیزیک یا تجربی از ریاضی و فیزیک و مکانیک اطلاعات داشته باشند . بنابراین قبل از توضیح این قسمت چند اصطلاح را در مکانیک دورانی شرح می دهیم .

۱) توضیح چند اصطلاح در مکانیک دورانی

در این قسمت توضیح کوتاهی راجع به محاسبات این آزمایش می دهیم برای فهم بهتر محاسبات انجام شده چند اصطلاح را در مکانیک دورانی توضیح می دهیم . توضیح کاملتر مکانیک دورانی در مقاله های “سینماتیک“  و “دینامیک” در این باره توضیح کافی داده می شود .
۱-۱) مکانیک دورانی : در انتقال کامل یک جسم (حرکت جسم) با حرکت خطی سرو کار داریم در مکانیک انتقالی با کمیت هائی مانند (سرعت و شتاب و جرم و…نیرو ) سرو کار داریم . حال اگر یک جسم سخت به جای حرکت انتقالی فقط دور یک محور بچرخد با حرکت دورانی و مکانیک دورانی سروکار داریم . کمیت ها و فرمول های مکانیک دورانی بسیار شبیه مکانیک انتقالی می باشد که در اینجا چند نمونه از کمیت های مکانیک دورانی ( سرعت زاویه ای و شتاب زاویه ای و… ) را شرح می دهیم .
۱-۲) سرعت زاویه ای : همانند سرعت خطی در حرکت انتقالی می باشد . و عبارت است از زاویه جابجا شده در واحد زمان که با ” θ  “ ( تتا ) نمایش می دهند .
۱-۳) شتاب زاویه ای : همانند شتاب خطی در حرکت انتقالی می باشد و عبارت است از مقدار تعغیر سرعت زاویه ای در واحد زمان که با “ω” ( امگا ) نمایش می دهند .
۱-۴) لختی دورانی : لختی دورانی یا ممان اینرسی معادل جرم در حرکت انتقالی می باشد و با “ I  ” نمایش می دهند.برای یک ذره کوچک و بدون بعد لختی دورانی برابر است با “حاصل ضرب جرم در مجذور فاصله از مرکز دوران” یک جسم بزرگ را می توان به تعداد بی شماری ذره کوچک تقسیم کرد و از طریق انتگرال گیری فرمول تبدیل جرم به لختی دورانی را بدست آورد.برای هر جسم بسته به که چه شکلی داشته باشد و محور دوران در کجای شکل باشد فرمول خاصی محاسبه می شود که مجموعه آن در جداول مخصوصی گرد آوری شده است که ما در اینجا وارد جزئیات آن نمی شویم .
۱-۵) گشتاور زاویه ای : گشتاور همان نقشی را در مکانیک دورانی بازی می کند که نیرو در مکانیک انتقالی بازی می کند فرمول آن هم از حاصل ضرب نیرو تا محور دوران بدست می آید . 

۲) نحوه محاسبات

برای اندازه گیری شتاب گرانشی به روش کاوندیش باید یکسری مقادیر معلوم را قبل از آزمایش اندازه بگیریم یکسری را در حین انجام آزماش و یک سری را بعد از پایان آزمایش اندازه گیری می کنیم . آنچه در اینجا ارائه می کنیم محاسبه مقادیر مجهول از روی مقادیر معلوم می باشد و با محاسبه همه مقادیر مجهول در نهایت ثابت گرانش محاسبه می شود . لازم به ذکر است که فرمول ها را به صورت کلی بدست می آوریم مقادیری که معلوم می باشد طبق “رابطه شماره ۱ ” ارائه شده است و بعد مرحله به مرحله کار را به پیش می بریم .
نکته : برای مشاهده یک مثال کاملا عددی و محاسبات آن به کتاب :
فیزیک هالیدی جلد اول(مکانیک ) ، صفحه ۳۹۲ ، مثال یک  مراجعه کنید .

۲-۱) مقادیر معلوم :مقادیری که معلوم بوده و یا مستقیما قابل اندازه گیری هستند به این صورت می باشند.

رابطه شماره ۱ – مقادیر معلوم در محاسبات تعیین ثابت گرانش

 ۲-۲) لختی دورانی دمبل : لختی دورانی دمبلی که دو گلوله انتهای آن جرم مساوی داشته باشند و فاصله گلوله ها از یکدیگر “L” باشد از این فرمول بدست می آید .

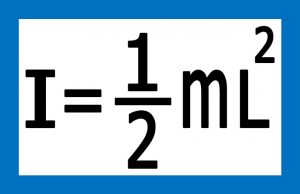
رابطه شماره ۲ – محاسبه لختی دورانی یا ممان اینرسی

نکته : لختی دورانی یا “ ممان اینرسی “  یک دمیل که دو کره انتهای آن با هم برابر باشند و جرم میله بین دو جسم در مقابل جرم دو کره قابل صرف نظر کردن باشد همیشه از این فرمول بدست می آید .
۲-۳) ضریب پیچشی ریسمان :  ضریب پیچشی ریسمان را به این طریق بدست می آوریم . ( شبیه رابطه بین دوره تناوب فنر و ثابت فنر در مکانیک انتقالی )

رابطه شماره ۳ – محاسبه ضریب پیچشی ریسمان ( شبیه ثابت فنر در مکانیک انتقالی )

۲-۴) محاسبه گشتاور  : رابطه میان گشتاور وارد شده و حداکثر زاویه چرخیده شده به این صورت است 🙁 شبیه رابطه بین نیرو و ثابت فنر در مکانیک انتقالی )

رابطه شماره ۴ – محاسبه گشتاور ایجاد شده

۲-۵) محاسبه نیرو از روی گشتاور : حال با داشتن گشتاور می توانیم نیروی گرانشی وارد بر دمبل ها را هم حساب کنیم . ( گشتاور برابر است با نیرو ضرب در بازوی گشتاور که در اینجا بازوی گشتاور نصف فاصله دمبل ها یعنی “L/2” است .)

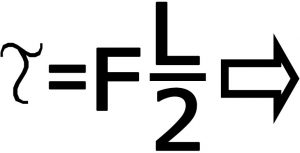
رابطه شماره ۵ – محاسبه نیروی عامل ایجاد گشتاور  ایجاد شده

۲-۶) محاسبه نیروی گرانشی وارد شده بر گلوله ها:برای محاسبه نیروی بین گلوله ها باید در نطر بگیریم که ماکزیمم نیروی گرانشی بین گلوله ها موقعی است که مراکز گلوله های بزرگ و کوچک کمترین فاصله را داشته باشند (فاصله r) بیائید مسئله را دقیق تر بررسی کنیم .
به طور خلاصه دمبل تحت تاثیر دو نیرو قرار می گیرد نیروی گرانشی و نیروی مقاومت ریسمان در برابر پیچیده شدن ابتدا نیروی گرانشی است که باعث چرخش دمبل می شود وقتی ریسمان به حداکثر پیچیدگی می رسد شروع به باز شدن می کند تا کاملا باز شود و بعد نیروی گرانشی دوباره ریسمان را می پیچاند بنابراین دمبل یک حرکت نوسانی انجام می دهد ( که از رابطه شماره ۳ ) بدست می آید ولی این نوسان کم و کمتر شده تا در نقطه ای که نیروی پیچشی ریسمان با گرانش گلوله ها برابر شود از نوسان می ایستد در این حالت فاصله “ r ” را اندازه گرفته و در روابط زیر می گذاریم . ( شکل شماره ۱۰ )

  

رابطه شماره ۶ – محاسبه نهائی ثابت گرانش

 

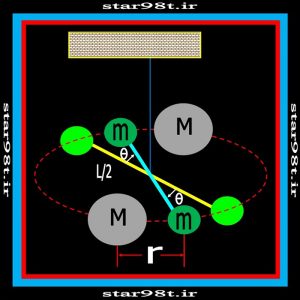
شکل شماره ۱۰ – محاسبه مقدار r

۷- محاسبه جرم زمین و خورشید

بعد از تعیین ثابت G حالا می توانستد جرم زمین و همینطور جرم حجمی زمین را حساب کنند علاوه بر آن از روی قانون سوم کپلر می شد جرم خورشید و همینطور سیارات دیگر منظومه شمسی را محاسبه کنند . در این بخش به محاسبه جرم زمین و خورشید می پردازیم .

۱) اهمیت جرم زمین

جرم زمین (Earth mass)، یا (M⊕) یکی از واحد های مهم جرم در نجوم می باشد . در اندازه گیری این واحد جرم اتمسفر زمین هم حساب می شود ولی جرم ماه حساب نمی شود . در ستاره شناسی جرم زمین کاربرد گسترده دارد و از آن برای نشان دادن جرم سیاره های دیگر مانند سیارات منظومه شمسی ( بخصوص سیارات سنگی ) و یا حتی سیارات فرا خورشیدی استفاده می شود . به این صورت که جرم سیارات را بر حسب مضربی از جرم زمین ارائه می کنند .

۲) محاسبه جرم زمین

زمین بر روی اشیاء اطراف زمین نیرو ی گرانش وارد می کند که ما آن را به صورت وزن حس می کنیم ( در رابطه با وزن و جرم در مقاله “نیروی جاذبه زمین” بخش چهارم« رابطه بین جرم و وزن »توضیح کافی خواهیم داد ) همچنین این نیرو را به صورت شتاب سقوط آزادحس می کنیم از این طریق براحتی می توان جرم زمین(Me) را محاسبه کرد .
فرض می کنیم جسمی به جرم m در مجاورت زمین سقوط آزاد می کند. می دانیم که شتاب سقوط آزاد برابر “g” می باشد و از طرفی این شتاب بعلت نیروی گرانش زمین است که از فرمول گرانش بدست می آید .
۱-۲) مقادیر معلوم : ابتدا مقادیر معلوم را می نویسیم .

 ۲-۲) محاسبات :  در این مرحله با توجه به شکل شماره ۱۱ جرم زمین را بدست می آوریم .

 

 

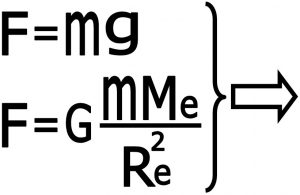
 شکل شماره ۱۱ – محاسبه جرم زمین

  ۳) اهمیت جرم خورشید

جرم خورشید (solar mass)، یا (M☉) هم ( مانند زمین ) یکی از واحد های مهم جرم در نجوم می باشد . در اندازه گیری این واحد جرم اتمسفر خورشید هم حساب می شود. در ستاره شناسی جرم خورشید کاربرد گسترده دارد و از آن برای نشان دادن جرم ستاره های دیگر و یا حتی جرم کهکشان ها استفاده می شود . به این صورت که جرم ستارگان را بر حسب مضربی از جرم خورشید ارائه می کنند .

۴) محاسبه جرم خورشید

برای محاسبه جرم خورشید باید نیروی گریز از مرکزی که زمین را در مدارش به دور خورشید نگه داشته مساوی نیروی گرانشی که بین زمین و خورشید می باشد قرار دهیم البته در این روش مدار زمین به دور خورشید را باید دایره حساب کنیم در حالی که بیضی می باشد ولی چون به دایره خیلی نزدیک می باشد می توانیم دایره بگیریم .
نکته : با دانستن جرم خورشید اطلاعات گرانبهائی نیز می توانیم در مورد ساختمان خورشید بدست بیاوریم که در مقاله های آینده در مورد آن توضیح خواهیم دارد .

۱-۲) مقادیر معلوم : ابتدا مقادیر معلوم را می نویسیم .

  

 ۲-۲) محاسبات : در این مرحله با توجه به شکل شماره ۱۲ جرم خورشید را بدست می آوریم .

 

 

 

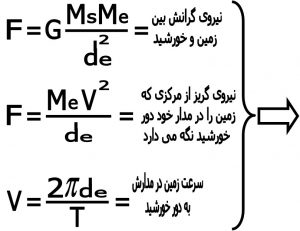
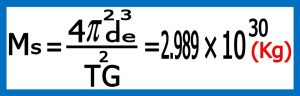
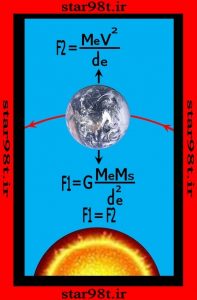
شکل شماره  ۱۲ – محاسبه جرم خورشید

برای مطالعه سایر مقاله های نجومی روی شکل زیر کلیک کنید.

برای مطالعه مقاله های روانشناسی اینجا  را کلیک کنید .

عکس های طبیعت, طبیعت خوانسار , شکوفه های بهاری  , گلستان کوه ,دانلود آلبوم های کامل بهترین و زیباترین عکس ها ,آلبوم هائی با صدها عکس کیفیت بالا ,  در هیچ کجای اینترنت این عکسها را پیدا نمیکنید , عکس هابدون استفاده از تکنیک های فتوشاپ تهیه شده , کاملا طبیعی 

برای آموزش کامل و حرفه ای گوگل مپ روی شکل زیر کلیک کنید

همه جیز در مورد گوگل مپ

۱) هر گونه اظهار نظر را در فرم اظهار نظر کاربران وارد کنید .
۲) نظرات بعد از تایید مدیریت نشان داده می شود .
۳) با انتقادات و پیشنهادات سازنده خود ما را هرچه بیشتر  همراهی کنید . مدیریت از انتقادات و پیشنهادات سازنده شما استقبال میکند .
۴) نوشته های قرمز پر رنگ ارجاع به لینک هستند که هنوز لینک آنها قرار داده نشده است ( هنوز صفحه آنها منتشر نشده است )
۵) نوشته های آبی پر رنگ ارجاع به لینک هستند که لینک آنها قرار داده شده است ( صفحه آنها منتشر شده است )
۶) هرگونه بهره برداری : کپی تمام و یا قسمتی از مطالب این سایت بدون ارجاع منبع آن ممنوع می باشد .
۷) تکثیر فایل های Pdf با ذکر منبع آزاد ولی فروش آن تحت هر عنوان و با ذکر منبع هم ممنوع می باشد.