در این مقاله به صورت مختصر تعدادی از فرمول های ریاضی و فیزیک را شرح می دهیم لازم به ذکر است فرمول ها و موارد شرح داده شده به صورت خیلی خلاصه بوده و اصولا این مقاله بخاطر استفاده در مقاله های مختلف فصل گرانش تهیه شده است این به آن معنی است که در قسمت ها و بخش هائی که نیاز به فرمول های پیچیده تر ریاضی و فیزیک می باشد و خواننده باید اطلاعاتی از این فرمول ها داشته باشدلینک آن را گذاشته ایم.تا با مراجعه به این مقاله بتواند مطلب را بهتر متوجه شود .
این به آن معنی نیست که همه فرمول های ریاضی و فیزیک را شرح داده ایم بلکه این مقاله خلاصه ای کوچک از این فرمول ها می باشد . لازم به ذکر است که حجم دانش های مربوط به فیزیک و ریاضی بسیار گسترده می باشد و توضیح آن در یک مقاله چند صفحه ای و یک یا چند کتاب امکان پذبر نمی باشد برای درک کامل مقالات فصل گرانش خواننده حداقل باید در سطح دیپلم ریاضی فیزیک اطلاعات از ریاضی و فیزیک داشته باشد .
۱- اهمیت فیزیک و ریاضی
اهمیت مطالعه طبیعت و شناخت قوانین طبیعت برکسی پوشیده نیست . تمام پیشرفت ها بشر در عرصه تکنولوژی و مهندسی بخاطر شناخت و بکارگیری نیروهای طبیعت است و شناخت نیروهای طبیعت هم با شناخت علوم تجربی امکان پذیر می باشد.از میان علوم مختلف تجربی یعنی علومی که با تجربه و آزمایش بدست آمده ( فیزیک ، شیمی ، زیست شناسی ، ستاره شناسی … زمین شناسی) که تکنولوژی ما هم بر روی آن بنا شده است . همه به همدیگر مربوط می باشند ولی تقریبا بیشتر علوم مختلف تجربی به فیزیک وابسته هستند در حالی که علم فیزیک به هیچکدام وابسته نیست . و فیزیک هم به ریاضی وابسته میباشد .
۱) فیزیک Physics
فیزیک (Physics ) علم مطالعه خواص طبیعت می باشد . علم ماده و رفتار آن در فضا و زمان می باشد . منظور از ماده می تواند کهکشان ها و ستارگان و اجرام بزرگ سماوی باشد یا اجسام معمولی که ما هر روزه می بینین و یا اجسام بسیار کوچک در حد اتم ها و ذرات زیر اتمی و… دانش فیزیک از مفاهیمی مانند سرعت و حرکت و… تا نیرو و انرژی و میدان های نیرو و… تا بارهای الکتریکی و موج و نور و …سایر مسائل صحبت می کند . بنابراین گستره دانش فیزیک بسیار وسیع می باشد . به صورت خیلی خلاصه :
هدف اصلی علم فیزیک بررسی و تحلیل طبیعت است و همواره این علم در پی آن است که رفتار طبیعت را در شرایط گوناگون درک و پیشبینی کند. پس همه علوم خواه ناخواه درگیر علم فیزیک می شوند .
۲) ریاضیات زبان طبیعت است
برای شناخت طبیعت و قوانین آن و کاربرد این قوانین در علوم گوناگون نیاز به دانش فیزیک می باشد ولی زبان طبیعت ریاضی می باشد و شناخت طبیعت بدون شناخت ریاضی ممکن نیست . بنابراین کسی که می خواهد در مورد قوانین طبیعت مطالعه کند باید با زبان ریاضی عمیقاً آشنایی داشته باشد .زیرا قوانین اساسی طبیعت را به هیچ طریقی نمیتوان بیان کرد مگر به زبان ریاضی؛ در واقع: ریاضیات زبان طبیعت است .
گالیله می گفت:«ریاضیات،زبان طبیعت است و برای شناخت طبیعت و آشنایی با قانون های حاکم بر آن،باید این زبان،یعنی ریاضیات را فرا گرفت.»
ازاین رو در دوران آموزش متوسطه فیزیک و ریاضی باهم تدریس می شود و دررشته های دانشگاهی مهندسی و… ریاضیات در سطح بالاتری هم به واحدهای درسی اضافه می شود .
۲- واحدهای اندازه گیری
سنگ بنا و ستون علم فیزیک کمیت های فیزیکی می باشد در فیزیک هر چیزی که مقدار آن با یک عدد مشخص شده و قابل اندازه گیری باشدکمیت فیزیکی نامیده می شود در این بخش به صورت خیلی مختصر در مورد کمیت های اصلی فیزیکی توضیح داده می شود.
توضیحات کاملتر در مقاله “مکانیک“ که در آینده منتشر می شود . داده می شود.
۱) کمیت های اصلی و فرعی
تعداد کمیت های فیزیکی خیلی زیاد است ولی مستقل از هم نیستند بنابراین از میان کمیت های فیزیکی چند کمیت را انتخاب می کنیم (هفت کمیت که مهمترین آنها : جرم و زمان و مسافت می باشد ) و کمیت های دیگر را از روی آنها تعریف می کنیم این کمیت ها را کمیت اصلی و کمیت هائی که از روی کمیت اصلی تعریف شده اند( مانندنیرو و انرژی و اندازه حرکت و…. ) را کمیت فرعی می نامیم .
کمیتهای فرعی بر اساس قوانین و فرمول های فیزیک ( روابط ریاضی بین کمیت ها ) بدست می آیند .
۲) چه کمیت هائی را به عنوان کمیت های اصلی انتخاب کنیم
حا سوال پیش می آید که در بین کمیت های مختلف چه کمیت هائی را به عنوان کمیت های اصلی در نظر بگیریم . مهمترین پاسخ این است که کمیت های اصلی را طوری باید انتخاب کنیم که ضمن این که کمترین تعداد از کمیت ها را انتخاب کردیم این تعداد بتواند توصیف کاملی از فیزیک بدهد .
۳) سیستم های مختلف اندازه گیری
برای انتخاب کمیت های اصلی و تعریف کمیت های فرعی از روی آن انتخاب های مختلفی وجود دارد و بر اساس آن تعدادی از کمیت ها را به عنوان کمیت های اصلی انتخاب می کنند . در اینجا چند عدد از سیستم های مختلف اندازه گیری را ذکر می کنیم .
۳-۱)سیستم SI (متریک MKS):سیستم متریک برای نخستین بار در سال۱۷۹۱بعد از پیروزی انقلاب فرانسه توسط لاوازیه (شیمی دان معروف) ارائه شد و نخست در فرانسه و بعد به تدریج در تمام کشورهای مختلف دنیا مورد استفاده قرار گرفت و هم اکنون در همه کشورهای جهان بجز آمریکا و لیبریا و برمه مورد استفاده قرار می گیرد . مهمترین کمیت های مورد استفاده در این سیستم (مترm- واحد طول) ، (کیلو گرم kg- واحدجرم) ،( ثانیهs – واحد زمان ) می باشد .
۳-۲) سیستم CGS : شبیه همان واحد SI بوده با یک تفاوت که بجای واحدهای اصلی SI واحدهای کوچکتر SI را به کار می برند کمیت های اصلی در این سیستم به این صورت است:(سانتی مترcm – واحد طول)،(گرم g – واحد جرم) ، (ثانیهs – واحد زمان) می باشد .
۳-۳) واحدهای انگیلیسی آمریکائی (US , UK ) : موقعی که سیستم بین المللی متریک آمد بسیاری از کشورها این سیستم را علی رغم سادگی آن نپذیرفتند و ترجیح دادند همان سیستم ملی و بومی خودشان را علی رغم پیچیدگی و غیر استاندارد بودن آن بکار ببرند یکی از این کشورها انگلستان بود که این سیستم علاوه بر انگلیس در سایر مستعمرات و بعد کشورهای مشترک المنافع به کار می رفت ولی سرانجام در همه کشورها حتی انگلیس (سال۱۹۹۵سیستم متریک را پذیرفت) کنار گذاشته شد ولی آمریکا هنوز از سیستم UK استفاده می کند . واحدهای اصلی در این سیستم (یارد yd- واحد طول)، (پوندib – واحد جرم) ، ( ثانیهs – واحد زمان ) می باشد .
۴) واحدهای بزرگتر و کوچکتر
برای هر کمیت اصلی یکسری واحدهای بزرگتر و کوچکتر هم وجود دارد . در سیستم متریک که بهترین و استاندارد ترین سیسم است واحدهای زیر مجموعه یک واحد اصلی به صورت دهدهی بوده ( واین یکی از مزیت های سیستم متریک به حساب می آید)درسیستم متریک این واحدها به صورت پیشوند هائی که ابتدای واحد گذاشته می شود تعریف می شود مثلا میلی یعنی یکهزارم بنابراین میلی متر یعنی یکهزارم متر و میلیگرم یعنی یکهزارم گرم و…. کیلو به معنی هزار بوده و کیلومتر یعنی هزار متر و کیلوگرم هزار گرم می باشد .
۵) کمیت های فرعی و هماهنگی واحدها
بعد از تعیین کمیت های اصلی نوبت به کمیت های فرعی می رسد . همانطور که گفته شد کمیت های فرعی همه وابسته به کمیت های اصلی هستند و در فرمول های فیزیک برای بدست آوردن جواب درست کمیت های فرعی باید از واحد اصلی کمیت های اصلی استفاده کنیم . مثلا واحد اصلی “طول متر” و واحد اصلی “زمان ثانیه” می باشد بنابراین واحد اصلی “سرعت متر بر ثانیه m/s “ می باشد در صورتی که بجای متر از کیلومتر و بجای ثانیه ازساعت استفاده کنیم سرعت بر حسب “کیلومتر بر ساعتKm/h بدست می آید که خب،اشکالی ندارد ولی اگر سرعت متغیر باشد و بخواهیم شتاب حاصله و بعد نیروی وارد شده را بر حسب نیوتن (که واحد اصلی نیرو می باشد) و… را محاسبه کنیم جواب های درستی بدست نمی آوریم پس باید توجه کنیم برای هماهنگی واحدها در حل اینگونه مسائل حتما باید از واحدهای اصلی هر کمیتی استفاده کنیم .
۶) تعیین استاندارد کمیت های اصلی
در سال ۱۷۹۵در فرانسه گروهی از دانشمندان جمع شدند تا برای کمیت های مهم و اصلی واحد انتخاب کنند . در ابتدا سه کمیت طول و جرم و زمان را به عنوان کمیت اصلی انتخاب کردند بعد نوبت به انتخاب واحد برای این کمیت ها رسید تعیین واحد اصلی هم فاکتورهائی را درنظرگرفت که اولا واحد اصلی تا حدود زیادی به واحدهای قبلی نزدیک بوده و بعدطوری تعریف شوند که انتخاب آن سلیقه ای نباشد و براساس پدیده ها و اشیائی باشد که باگذشت زمان تعغیر نکند بنابراین پدیده هائی را در نظر گرفتند که بیشترین نقش را در زندگی ما بازی کنندو بعد از تعیین واحد یک نمونه ازآن (واحدهای طول وجرم) را ساخته و در مرکزی خاص نگه داری کردند( اداره بین المللی اوزان و مقادیر) و از روی آن نمونه های دقیقی ساخته و به سراسر دنیا فرستادند .
۷) اداره بینالمللی اوزان و مقیاسها BIPM
اداره بینالمللی اوزان و مقیاسها( International Bureau of Weights and Measures) یکی از سه سازمانی است که برای نگهداری از سیستم استاندارد یکاها (SI) پایه گزاری شده است . این سازمان در سال ۱۸۷۵و پس از امضای پیمان متر، ایجاد شد. مقر آن در هم اینک شهر پاریس قرار دارد .

شکل شماره ۱- اداره بینالمللی اوزان و مقیاسها

شکل شماره ۲- آرم اداره اوزان و مقیاس ها
۸) استاندارد طول
برای اولین بار بعد از پیروزی انقلاب کبیر فرانسه دولت وقت تصمیم گرفت سیستم جدیدی پایه گزاری کند که هیچ ارتباطی با سیستم پادشاهی منحل شده نداشته باشد و همانطور که شرح آن رفت دقیق بوده و بر مبنای مهمترین پدیده ها و مقادیر زندگی بشر باشد. از این رو دولت وقت فرانسه از چهاردانشمند مشهور (بوردا، لاگرانژ،لاپلاس و کوندورسه )دعوت کرد تا روی این موضوع کار کنند آنها یک چهل میلیونیم محیط نصف النهار زمین را که از شهر پاریس عبور کرده به نام متر انتخاب کردند( البته بعدها نصف النهار مبدا شد) و نه سال بعد دو منجم فرانسوی، دالامبر و میشن، این مقدار را بطور دقیق اندازهگیری کردند .
توضیحات بیشتر را در مقاله “ مکانیک “ بخش اندازه گیری می دهیم .

شکل شماره ۳ – متر استاندارد
۹) کیلوگرم نمونه
در همان زمان انقلاب فرانسه که می خواستند واحدها را عوض کنند تصمیم گرفتند یک واحد جدید هم برای جرم بسازند از این رو یک دسیمتر مکعب (یک لیتر ) آب مقطر در دمای۲۰درجه را در نظر گرفته و جرم این مقدار آب را یک کیلوگرم Kg نامیدند . بنابراین یک استوانه ای از جنس پلاتین (که بعدها با استوانه ای از جنس پلاتین ایریدیوم تعویض شد)ساخته و برای جلوگیری از نشستن گرد و غبار و آلودگی های موجود درهوا درمجموعه ای ازحفاظ های تو در تو قرار داده قرار داده که در ادارهٔ بینالمللی اوزان و مقیاسها در شهرِ سور، در حومهٔ پاریس نگهداری کردند. مدتی بعد دانشمندان دیدند که از جِرم این میله کاسته میشود! به همین دلیل، دانشمندان در حال ساخت کُره ای از جنس کریستال هستند که جِرمش یک کیلوگرم باشد.

شکل شماره ۴ – کیلوگرم نمونه
۱۰) واحد زمان
ثانیه یکای زمان درسیستم متریک یا دستگاه SI بوده و نشانه ی آن S یا Sec است.ثانیه میتواند توسط ساعت مکانیکی، الکتریکی یا اتمی اندازهگیری شود.یک ثانیه بنابر تعریف ۸۶۴۰۰/۱شبانه روزمتوسط خورشیدی می باشد.ثانیه علاوه بر دستگاه متریک در دیگر سامانههای اندازهگیری نیز به عنوان یکا استفاده میشود. (به طور مثال دستگاه واحدهای سانتیمتر-گرم-ثانیه) همچنین ثانیه مبنایی برای تعریف دیگر یکاها نیز قرار گرفتهاست. به طور مثال تعریف متر بر اساس تعریف ثانیه و سرعت نور است.
نکته : تعاریفی که در اینجا در باره ثانیه و متر به کار بردیم در نیمه دوم قرن بیستم دچار تحول اساسی شد به گونه ای که بجای تعاریف قدیمی تعریف جدید بر مبنای فیزیک اتمی و همینطور سرعت نور دوباره تعریف شد . در مقاله “ مکانیک “ در این باره توضیحات کاملتر می دهیم .
۳- بردار چیست ؟
بردارها در ریاضی و فیزیک و مهندسی بسیار مهم هستند زیرا بسیاری از کمیت های فیزیکی (کمیت فیزیکی به ویژگی هائی می گویند که قابل اندازه گیری باشند)باید با بردار نشان داده شده ومحاسبات و اندازه گیری روی آنها با کمک بردار باشد.( شکل شماره ۵)
در این بخش فقط توضیح بسیار کوتاهی در مورد بردارها می دهیم توضیح کاملتر در مقاله “ مکانیک “ داده می شود .

شکل شماره ۵ – مفهوم بردار
۱) جمع و تفریق بردارها
بردارها نیز مانند اعداد با هم جمع و تفریق می شوند.برای جمع و تفریق بردارها ابتدای آنها را به یک نقطه منتقل کرده (یک نقطه را در نظر گرفته و برداری هم اندازه و موازی دو بردار رسم می کنیم) و دو بردار را دو ضلع متوازی الاضلاع درنظر گرفته و طبق شکل شماره ۶ مجموع و تفاضل ٖآنها را بدست می آوریم .
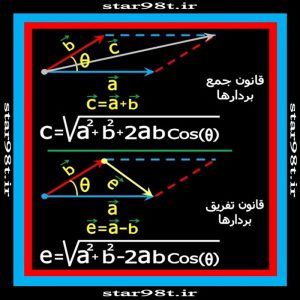
شکل شماره ۶ – جمع و تفریق بردارها
۲) تجزیه بردارها
بسیاری از موارد لازم می شود یک بردار به دو موئلفه تجزیه شود . این بیشتر در مورد نیروها به کار می رود شکل و فرمول آن مطابق شکل ۷ می باشد .

شکل شماره ۷ – تجزیه بردارها
۳) کمیت های برداری و اسکالر
کمیت های فیزیکی (در فیزیک هر چه قابل اندازه گیری باشد کمیت نامیده می شود) به دو گروه تقسیم می شوند کمیت های اسکالر و کمیت های عددی
۳-۱) کمیت های اسکالر و یا نرده ای: کمیت های اسکالر ((Scalar به کمیت هائی گفته می شود که فقط دارای اندازه باشند و جهت نداشته باشند . مانند : زمان، طول،حجم ،جرم و…
۳-۲) کمیت های برداری : بردار به معنی پاره خط جهت دار می باشد و کمیت های برداری کمیت هائی هستند که علاوه بر اندازه دارای جهت نیز می باشند . مانند : نیرو ، سرعت ، شتاب و… کمیت های اسکالر را تنها با یک حرف انگلیسی نشان می دهند در حالی که کمیت های برداری با یک حرف که روی آن یک فلش می باشد نشان می دهند .
نکته : در فرمول های فیزیک بیشتر مواقع فقط اندازه یک کمیت برداری مورد نظر می باشد و مقدار آن مورد نظر نیست در این صورت به طور خیلی ساده فقط فرمول را می نویسند جائی که نیاز به جهت هم باشد روی کمیت مورد نظر یک “فلش “ قرار داده که به معنی آن است که جهت کمیت هم برای ما مهم می باشد .
۴) ضرب بردارها
همچنین می توان بردارها را هم در یکدیگر ضرب کرد که در این بخش در مورد آن توضیح نمی دهیم . و در آینده در مقاله “ بردارها “ در مورد آن توضیح کامل می دهیم .
۴- مروی بر بعضی از مفاهیم مکانیک
مکانیک شاخه ای از دانش فیزیک می باشد که به مطالعه ماده و نیروهائی که باعث حرکت آن می شود اقدام می کند . دانش مکانیک در مورد مسائل مختلفی مانند حرکت و سرعت و شتاب و… گفتگو می کند و سابقه آن به دوران کهن و ماقبل تاریخ برمی گردد .
در این بخش توضیح کوتاهی در مورد فرمول های مکانیک که در مقاله های مختلف گرانش استفاده می شود می دهیم . و توضیحات کاملتر و جامعتر را در آینده در مقاله “ مکانیک “می دهیم
۱) سرعت
به صورت خیلی ساده سرعت مسافت پیموده شده در واحد زمان می باشد . سرعت یک کمیت برداری می باشد یعنی علاوه بر مقدار جهت هم دارد . اگر حرکت مستقیم الخط یکنواخت باشد سرعت (ازنظر اندازه و جهت ) مقدار ثابتی می باشد در غیراین صورت سرعت متغیر بوده و ما هر لحظه یک سرعت داریم که سرعت لحظه ای نامیده می شود و اگر کل مسافت را بر زمان پیموده شده تقسیم کنیم سرعت متوسط را داریم .

۲) شتاب
در فیزیک شتاب را مقدار تعغیر سرعت در واحد زمان تعریف می کنند . از آنجائی که سرعت کمیت برداری می باشد شتاب هم کمیت برداری می شود . اگر سرعت از نظر اندازه تعغیری نکند ولی از نظر جهت تعغیر کند باز هم حرکت شتابدار خواهیم داشت .


۳) نیرو و قوانین حرکت
در اصطلاح عامیانه نیرو به معنی هل دادن و کشیدن معنی می شود ولی در فیزیک تعریف دقیق تری موجود می باشد . در فیزیک “نیرو به معنی عاملی است که باعث شتاب ذره می شود« این تعریف دقیقا از روی قانون دوم نیوتن بدست آمده است» . پس هم اکنون قوانین حرکت نیوتن را می آوریم .
۳-۱) قانون اول نیوتن : اگر بر جسمی نیرو وارد نشود (ویا برآیند نیروهای وارد به آن صفر باشد) آن جسم حرکت یکنواخت مستقیم الخط (سرعت از نظر اندازه و جهت تعغیر نمی کند) خود را حفظ می کند .
۳-۲) قانون دوم نیوتن : اگر بر جسمی نیرو وارد شود (ویا برآیند نیروهای وارد به آن صفر نباشد) آن جسم در امتداد نیرو (و یا برآیند نیرها ) شتاب می گیرد که مقدار شتاب از رابطه زیر بدست می آید .
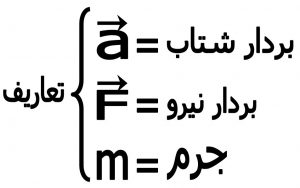
 ۳-۳) قانون سوم نیوتن : برای هر عملی (نیروی عمل) عکس العملی موجود است مساوی و خلاف جهت آن
۳-۳) قانون سوم نیوتن : برای هر عملی (نیروی عمل) عکس العملی موجود است مساوی و خلاف جهت آن
نکته مهم : نیروهای عمل و عکس العمل به دو جسم متفاوت وارد می شوند و گرنه ما حرکت شتابدار نداشتیم . چرا؟

۴) سینماتیک و دینامیک
مکانیک کلاسیک با اجسام در حال سکون و حرکت، تحت تأثیر نیروهای داخلی و خارجی سرو کار دارد. مکانیک به دو دسته سینماتیک و دینامیک تقسیم می شود.که در اینجا توضیح بسیار کوتاهی در موردآن می دهیم .
۴-۱) سینماتیک : سینماتیک (به معنای حرکتکردن) شاخهای از دانش مکانیک کلاسیک است که حرکت اجسام و سامانهها (گروهی از اجسام) را بدون درنظرگرفتن نیروهای عامل حرکت بررسی میکند.
۴-۲) دینامیک : وقتی عامل حرکت یعنی نیرو را بررسی می کنیم و نیروهای داخلی و خارجی وارد شده به اجسام را مورد بررسی قرار می دهیم با دینامیک سرو کار داریم . ساده ترین قوانین دینامیک همان قوانین حرکت نیوتن می باشد که در قسمت قبلی مورد بررسی قرار دادیم .
۵) معادلات حرکت
وقتی از حرکت صحبت می کنیم اولین مسئله جابجائی جسم می باشد ساده ترین حالت این است که این جابجائی با سرعت ثابت و در امتداد خط راست می باشد که به آن حرکت مستقیم الخط یکنواخت می گویند ولی حرکت حالت های پیچیده تری هم دارد می تواند این حرکت با شتاب ثابت ولی مستقیم الخط باشد و می تواند با شتاب متغیر باشد همچنین حرکت می تواند بجای مستقیم الخط بودن در دو بعد(درون صفحه)وحتی سه بعدی باشد .
بنابراین می بینیم جسم می تواند انواع حرکت ها از حرکت مستقیم الخط یکنواخت تا حرکت دو یا سه بعدی با شتاب متغیر را داشته باشد در این صورت مسیر حرکت به صورت خط راست یا یک منحنی خواهد شد و معادله این منحنی در سیستم مختصات معادله حرکت جسم نامیده می شود .
می توانیم جابجائی را در محورهای XوYوZبه صورت جداگانه بر حسب پارامتر زمان(t) هم بنویسیم . معادلات حرکت نقش بسیار مهمی در توضیح و تفسیر حرکت همچنین پیش بینی مسیر حرکت دارد .
۶) سقوط آزاد
در صورتی که یک جسم را در ارتفاع معینی (ارتفاع h)در اطراف زمین رها کنیم . و از مقاومت هوا و نیروهای دیگر (وزش باددر راستای افقی و…) صرف نظر کنیم . جسم در راستای عمودی و تنها تحت تاثیر وزن خود با شتاب ثابت “g” (که مقدار آن حدود ۸/۹ می باشد) به سمت زمین سقوط می کند بنابراین سقوط آزاد نوعی حرکت شتابدار (با شتاب ثابت g) می باشد که در راستای عمودی ( محورY) انجام می شود .
۷) حرکات پرتابی
در صورتی که یک جسم تنها تحت تاثیر نیروی جاذبه بوده ( از مقاومت هوا صرف نظر شود ) و فقط در راستای عمودی پرتاب شود و یا از ارتفاع معینی رها شود با حرکت سقوط آزاد با شتاب ثابت g سروکار داریم ولی در بیشتر مواقع یک جسم تحت زاویه ای (مانندθ) پرتاب می شود در این صورت حرکت در دو بعد صورت می گیرد ( با صرف نظر کردن از مقاومت هوا ) می توانیم حرکت جسم را به دو حرکت جداگانه تقسیم کرده و هر کدام را بر حسب پارامتر t (زمان) بنویسیم .حرکت افقی حرکت مستقیم الخط یکنواخت (با سرعت ثابت) و حرکت عمودی (حرکت شتابدار با شتاب ثابت g) و یا با حذف پارامتر t رابطه بین xوyرا به عنوان معادله حرکت پرتابی بنویسیم. بنابر این در حرکات پرتابی سرعت اولیه “V0” (سرعتی که جسم را با آن پرتاب کردیم ) را ابتدا باید به دو موئلفه سرعت در راستای محور X یعنی (Vx) و سرعت در راستای محور Y یعنی (Vy) تجزیه کرده تا بتوانیم معادلات سرعت را بنویسیم ( توضیح کاملتر و فرمول های مربوطه در مقاله “ مکانیک “ می باشد )
۸) نیروی گریز از مرکز و جانب مرکز
نیروی جانب مرکز (مرکز گرا)نیروئی است که به یک جسم درحال دوران وارد می شود (مانند نیروی گرانش ، کشش طناب و…) اگر جسم درحال حرکت مستقیم الخط یکنواخت باشدحرکت جسم به حرکت دورانی تبدیل شده و از حرکت مستقیم الخط جسم جلوگیری می کند . بنابر این به نظر می رسد نیروی جانب مرکز از طرف نیروی دیگری به نام “نیروی گریز از مرکز “ خنثی شده و جسم به حال تعادل می رسد . درحالی که باید بدانیم نیروی گریز از مرکز یک نیروی واقعی نیست و شبه نیرو می باشد.(در این مورد در مقاله “ مکانیک “ بیشتر توضیح داده می شود) مقدارنیروی گریز ازمرکز طبق فرمول زیر بدست می آید.



شکل شماره ۸ – نیروی گریز از مرکز زمین را در مدار خود نگه می دارد
نکته : این فرمول را هم می توانستیم مانند فرمول های قبل به صورت برداری بنویسیم ولی برای سادگی کار فرمول را به صورت اسکالر نوشتیم از اینجا به بعد هر جا فقط نیاز بود فرمول ها را به صورت برداری می نویسیم .
۹) کار و انرژی
در مکانیک کار عبارت است از حاصل ضرب نیرو در جابجائی در راستای نیرو یعنی : W=F*d ( که در آن F نیروی وارد شده بر جسم و d جابجائی در راستای نیرو و W کار انجام شده روی جسم می باشد) نکته بسیار مهم این است که نیرو باید در راستای جابجائی باشد تا کاری صورت بگیرد در غیر این صورت کاری انجام نمی شود .
تعاریف گوناگونی در مورد انرژی وجود دارد ولی مهمترین تعریف انرژی را توانائی انجام کار می گویند یعنی انرژی عاملی است که می تواند کار (در اصطلاح مکانیکی آن) انجام دهد. نکته مهم این است که ماهیت کار و انرژی یکسان بوده هر دو کمیت هائی اسکالر (اندازه بدون جهت) بوده و واحد هر دو یکی می باشد ( ژول J )
انرژی انواع مختلف دارد و یک از انواع انرژی ها انرژی مکانیکی می باشد که در دو نوع ظاهر می شود .
۹-۱) انرژی جنبشی : انرژی جنبشی یکی از صورتهای انرژی است که جسم بخاطر حرکت دارا میباشد. انرژی جنبشی یک جسم با جرم جسم و مجذور سرعت رابطه مستقیم دارد. E=(1/2)mV2
۹-۲) انرژی پتانسیل : در مکانیک انرژی پتانسیل ( K ) صورتی از انرژی است که قابلیت تبدیل شدن به انرپی جنبشی را دارا باشد به عبارت دیگر انرژی ذخیره شده در جسم می باشد .
نکته بسیار مهم این است که انرژی جنبشی و پتانسیل موجود در یک جسم همواره ثابت می باشد بنابراین با کاهش انرژی پتانسیل انرژی جنبشی افزایش پیدا می کند و برعکس
۱۰) مرکز جرم
مرکز جرم) (Center of massیک جسم صلب(جسم سخت)یا مجموعه ای از اجسام که یک سیستم را تشکیل می دهند نقطه مشخصی در درون(جسم یا سیستم) می باشد که گوئی همه جرم آن جسم (یا سیستم) در آن نقطه متمرکز شده است . پس در هر جسم صلب نقطه ای به نام مرکز جرم وجود دارد که گرانیگاه (نقطه تعادل)هم نامیده می شود (زیرا اگر جسم را از آن نقطه آویزان کنیم حالت تعادل پیدا می کند) و نقطه اثر نیروی گرانش و یا نیروهای دیگری می باشد مثلا گرانیگاه یک کره متقارن (جرم حجمی همه قسمت های آن یکی باشد ) در مرکز کره و مرکز جرم یک دیسک دایره ای تخت مرکزدیسک و مثلث نقطه برخورد میانه ها می باشد.
۵- مقاطع مخروطی
وقتی یک صفحه مخروط دواری را قطع می کند بسته به سطح مقطع قطع شده شکلی که تشکیل می شود یکی از اشکال (دایره ، بیضی ، سهمی و هذولی) می باشد به همین خاطر در هندسه این اشکال را مقاطع مخروطی می نامند . در این بخش توضیح بسیار مختصری در مورد مقاطع مخروطی می دهیم . مطالب این بخش بر اساس مقاله “ مقاطع مخروطی “تهیه شده است بنابراین برای مطالعه بیشتر به این مقاله که در همین سایت منتشر شده است مراجعه کنید .
۱) اهمیت مقاطع مخروطی
مقاطع مخروطی در بسیاری از علوم ( مانند نجوم مبحث مربوط به گرانش) کاربرد دارد.برای مثال برای محاسبه مسیرحرکت اجرام آسمانی به مقاطع مخروطی نیاز داریم . نیروهای مختلفی به اجرام آسمانی وارد می شود که ناشی از تاثیر گرانش است بر حسب سرعت و جهت ، این نیروها مسیرهای مختلفی به اجرام آسمانی می دهند دانشمندان در صفحه ای که این اجرام حرکت می کنند معادله مسیرحرکت را نوشته و ثابت می کنند این معادله یکی از مقاطع مخروطی می باشد. بنابراین درک مکانیک سماوی (حرکت اجرام آسمانی ) بدون شناخت معادلات مقاطع مخروطی امکان پذیر نمی باشد در مقاله “قوانین کپلر و حرکت مداری” با استفاده از قانون جاذبه عمومی و حساب دیفرانسیل و انتگرال معادله حرکت سیاره ها را به دور خورشید نوشته و ثابت می کنیم این معادله یک بیضی می باشد .
۲) مخروط دوار
اگر دو خط متقاطع در یک صفحه داشته باشیم و یکی از خطوط دور خط دیگر شروع به دوران کند دو مخروط بی انتها بدست می آید که از طرف راس به هم چسبیده اند .
خطی که دوران حول آن صورت گرفته خط محور مخروط و خطی که دوران کرده مولد مخروط نامیده می شود .
برای توضیح کاملتر در مورد مخروط و مخروط دوار به مقاله “ مخروط “ مراجعه کنید .
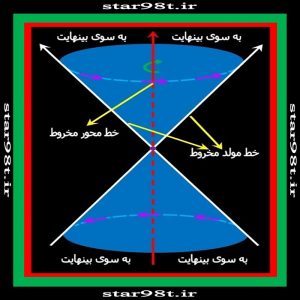
شکل شماره ۹ – مخروط دوار
۳) مقاطع مخروطی چگونه بوجود می آید ؟
در صورتی که یک مخروط دواردر فضا داشته باشیم و صفحه ای این مخروط را قطع کند بسته به این که چگونه و با چه زاویه ای مخروط را قطع کند شکل های مسطحی (دایره ، بیضی ، سهمی و هذولی) در صفحه پدید می آید که به آن مقاطع مخروطی می گویند. ( شکل شماره ۱۰ )
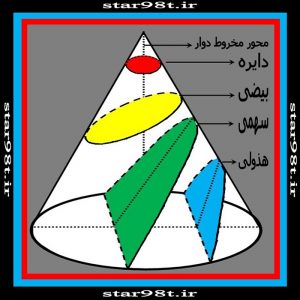
شکل شماره ۱۰ – مقاطع مخروطی
۴) تاریخچه مقاطع مخروطی در دوران باستان
مقاطع مخروطی کاربرد بسیار زیادی در علوم و تکنولوژی دارد.شناخت مقاطع مخروطی از زمان یونان باستان با کتاب مخروطات آپولونیوس (درحدود ۲۰۰ قبل از میلاد) شروع شد .ولی این کتاب به فراموشی سپرده شد و در دوران طلائی اسلام سه دانشمند به نام های “برادران بنوموسی “ دوباره با ترجمه کتاب “آپولونیوس “بحث مقاطع مخروطی را زنده کردند کتاب“برادران بنوموسی“دردوره رنسانس به اروپا رسید واین بحث گسترش یافت.
۶- معادله مقاطع مخروطی
مقاطع مخروطی (دایره ،بیضی ، سهمی و هذولی) همانند هر شکل دیگری در سیستم های مختلف مختصات، معادله جبری مربوط به خودشان را دارند به گونه ای که با رسم این معادلات در سیستم های مختلف می توان آن شکل را بدست آورد . همانطور که در بخش قبلی گفته شد در مبحث گرانش و در اثبات قوانین کپلر به معادلات مقاطع مخروطی نیاز داریم در این بخش به طور خیلی مختصر معادلات مقاطع مخروطی را توضیح می دهیم . برای توضیحات کاملتر به مقاله “معادله مقاطع مخروطی “از همین بخش مراجعه کنید .
۱) صورت کلی معادلات درجه دوم
یک معادله درجه دوم برحسب (yوx) یک معادله جبری است که در آن (yوx) محهول و بقیه حروف در واقع پارامتر یا اعداد مشخص می باشند (در صورتی که اعداد را با پارامتر نشان دهیم تعداد نامحدودی معادله و شکل بدست می آید و در صورتی که بجای پارامتر فقط اعداد مشخص باشند تنها یک شکل بدست می آید ) صورت کلی معادلات درجه دوم بر حسب (x,y) به این صورت است .
![]()
۲) تبدیل معادلات درجه دوم به معادلات گسترده مقاطع مخروطی
معادله گسترده فوق تحت شرایطی به معادلات گسترده مقاطع مخروطی تبدیل می شوند. اثبات این مسئله در مقاله “معادله مقاطع مخروطی “ توضیح داده شده است و در اینجا فقط صورت معادلات گسترده مقاطع مخروطی را در جدول شماره یک توضیح می دهیم .
جدول شماره یک – صورت کلی معادلات گسترده مقاطع مخروطی
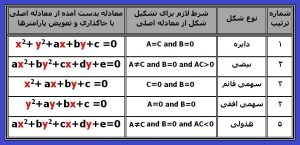
۳) معادلات کانونیک مقاطع مخروطی
معادلاتی که به عنوان معادلات گسترده مقاطع مخروطی در جدول شماره یک آمده است . جزئیات مقاطع مخروطی (مرکز و کانون و خط هادی و…راس)را مشخص نمی کند . بنابراین به معادلاتی نیاز داریم تا مشخصات وجزئیات مقاطع مخروطی را مشخص کند . این معادلات را معادله کانونیک مقاطع مخروطی می نامیم . که در جدول شماره ۲فهرست شده اند.براحتی می توان ازمعادلات کانونیک معادلات گسترده را بدست آوردو همچنین ازمعادلات گسترده معادلات کانونیک را بدست آورد.که توضیح کامل و اثبات فرمول ها در مقاله “معادله مقاطع مخروطی “آمده است و ما در اینجا فقط فرمول های معادلات کانونیک را در جدول شماره دو آوردیم .
جدول شماره ۲ – صورت کلی معادلات کانونیک مقاطع مخروطی

۴) معادلات قطبی مقاطع مخروطی
در بسیاری از موارد بهتر است بجای معادله منحنی ها در مختصات دکارتی معادله در سیستم قطبی نوشته شود . سیستم مختصات قطبی نخستین بار توسط نیوتن برای اثبات قوانین کپلر به کار گرفته شد . هر چند شواهدی در دست است که نشان می دهد این دستگاه نخستین بار توسط ابوریحان به کار گرفته شده است .
در سیستم مختصات قطبی یک نقطه به نام مبدا داشته و بجای دو محور تنها یک محور داریم و مختصات هرنقطه را با فاصله از مبدا و زاویه ای که “پاره خط بین آن نقطه و مبدا مختصات” با محور در جهت خلاف عقربه های ساعت می سازد ( شکل شماره ۱۱ ) همچنین در شکل شماره ۱۲ مختصات قطبی مقاطع مخروطی رسم شده است .
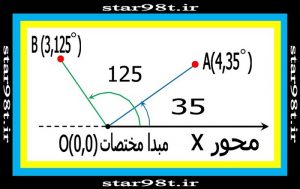
شکل شماره ۱۱ – محورهای مختصات قطبی

شکل شماره ۱۲ – معادله قطبی مقاطع مخروطی
۷- مختصری از حساب دیفرانسیل و انتگرال
توضیح کامل حساب دیفرانسیل و انتگرال بسیار پیچیده بوده و در این مقاله نمی گنجد . دانش آموزان رشته ریاضی فیزیک و دانشجویان رشته های مهندسی با این قسمت از ریاضیات باید آشنائی داشته باشند ما در اینجا فقط توضیح بسیار کوتاهی راجع به مبانی علم حسابان (دیفرانسیل و انتگرال و مشتق)می توانیم بدهیم.
حسابان یکی از شاخه های ریاضیات است وحساب دیفرانسیل و انتگرال یکی ازشاخه های حسابان میباشد که خود به دو قسمت تقسیم می شود. حساب دیفرانسیل که به مطالعهٔ نرخ تغییرات کمیتها میپردازد. نرخ تعغیرات تابع (کمیت ها)در هر نقطه دلخواه را مشتق و فرایند یافتن مشتق را مشتق گیری می نامند. در قضیهٔ اساسی حسابان ثابت می شود که انتگرال گیری عکس مشتق گیری می باشد . انتگرال خود به دو نوع انتگرال معین و انتگرال نامعین تقسیم می شود (همینطور انتگرال های دو گانه و چند گانه هم داریم ) که انتگرال معین به عنوان سطح زیر منحنی به کار می رود . حسابان درفیزیک و مکانیک و مهندسی وحتی پزشکی و…علوم مختلف کاربرددارد. از جمله کاربردهای مشتق در مکانیک می توان به این موارد اشاره کرد : سرعت لحظه ای مشتق مسافت نسبت به زمان و شتاب لحظه ای مشتق سرعت نسبت به زمان می باشد
توضیحاتی که در این بخش داده می شود فقط محض آشنائی خوانندگان با مفاهیم دیفرانسیل و مشتق و انتگرال می باشد و امکان توضیح کامل در این مختصر وجود ندارد توضیح بیشتر را در مورد حساب دیفرانسیل و انتگرال در مقاله “حساب دیفرانسیل و انتگرال “ که در آینده منتشر می شود می دهیم .
۱) دیفرانسیل
هر تعغیر جزئی (بسیار کوچک نزدیک به صفر ونه خودصفر )را درتابع (تابع مجموعه ای از زوج های مرتب “ “ x,y است که به ازاء هر x فقط یک yداشته باشیم ) ، وقتی متغیر تابع تعغیرات (بسیار جزئی) می کند را دیفرانسیل می گویند. از این رو حساب دیفرانسیل ، حساب تعغیرات بسیار جزئی می باشد بنابراین وقتی داشته باشیم : y=F(x) می توانیم بنویسیم .

۲) مشتق
اگر تابع F(x) را داشته باشیم مشتق تابع F(x) که با ” “ F’(x) و “ y’ “ نشان می دهند عبارت است از :
برای تابع های مختلفی که با ضابطه های خاصی بیان می شوند فرمول های مختلفی برای مشتق آنها وجود دارد که که در اینجا دیگر به آنها نمی پردازیم . دو تعریف برای مشتق داریم .
۲-۱) تعریف اول : مطابق فرمول زیر است .
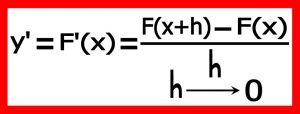
۲-۲) تعریف دوم : طبق فرمول زیر است
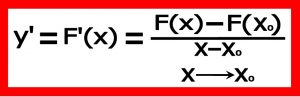
و یا دقیق تر بخواهیم بنویسیم .

۳) انتگرال نامعین
ساده ترین تعریف انتگرال این است که انتگرال عکس مشتق گیری می باشد همچنین انتگرال را می توان به انتگرال معین و غیر معین تقسیم بندی کرد . بنابراین ساده ترین فرمول هائی که برای انتگرال بیان می شود را به این صورت می توان نشان داد .

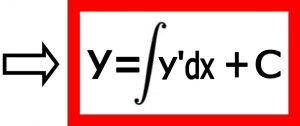
Cعدد دلخواهی می باشد که در انتگرال نامعین ظاهر می شود ولی در انتگرال معین ظاهر نمی شود.
۴) انتگرال معین
انتگرال نامعین شبیه همان انتگرال معین است با این تفاوت که با جاگزاری دو مقدار عددی یک عدد ثابت بدست می آید ( می توانیم به جای دو عدد دو پارامتر بگذاریم یا حتی دو تابع قرار دهیم ولی منظور از انتگرال معین جاگذاری دو عدد می باشد ) تعبیر هندسی انتگرال معین مساحت زیر منحنی یک تابع می باشد . انتگرال معین در بسیاری از موارد در علوم و تکنولوژی کاربرد گسترده دارد .
۵) فرمول انتگرال معین
فرمول انتگرل معین به این صورت می باشد .
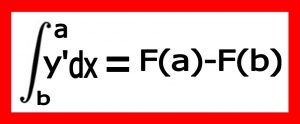
بحث و توضیح کامل در مورد انتگرال دراین مقاله نمی گنجد و در مقاله “حساب دیفرانسیل و انتگرال “ در آینده توضیح کاملتر می دهیم .
![]()
برای مطالعه سایر مقاله های نجومی روی شکل زیر کلیک کنید.
![]()
برای مطالعه مقاله های روانشناسی اینجا را کلیک کنید .
![]()
عکس های طبیعت, طبیعت خوانسار , شکوفه های بهاری , گلستان کوه ,دانلود آلبوم های کامل بهترین و زیباترین عکس ها ,آلبوم هائی با صدها عکس کیفیت بالا , در هیچ کجای اینترنت این عکسها را پیدا نمیکنید , عکس هابدون استفاده از تکنیک های فتوشاپ تهیه شده , کاملا طبیعی
![]()
برای آموزش کامل و حرفه ای گوگل مپ روی شکل زیر کلیک کنید
![]()
۱) هر گونه اظهار نظر را در فرم اظهار نظر کاربران وارد کنید .
۲) نظرات بعد از تایید مدیریت نشان داده می شود .
۳) با انتقادات و پیشنهادات سازنده خود ما را هرچه بیشتر همراهی کنید . مدیریت از انتقادات و پیشنهادات سازنده شما استقبال میکند .
۴) نوشته های قرمز پر رنگ ارجاع به لینک هستند که هنوز لینک آنها قرار داده نشده است ( هنوز صفحه آنها منتشر نشده است )
۵) نوشته های آبی پر رنگ ارجاع به لینک هستند که لینک آنها قرار داده شده است ( صفحه آنها منتشر شده است )
۶) هرگونه بهره برداری : کپی تمام و یا قسمتی از مطالب این سایت بدون ارجاع منبع آن ممنوع می باشد .
۷) تکثیر فایل های Pdf با ذکر منبع آزاد ولی فروش آن تحت هر عنوان و با ذکر منبع هم ممنوع می باشد.
![]()