با توجه به این که ما در روی کره ای به نام زمین زندگی می کنیم و همچنین برای حل بسیاری از مسایل ستاره شناسی, می توانیم تمام اجرام سماوی را روی یک کره فرضی بنام کره سماوی در نظر بگیریم بنابر این نیاز به شاخه ای از هندسه به نام هندسه کروی احساس می شد . قبل از آن که در مورد هندسه کروی بحث کنیم کمی در مورد هندسه مسطحه یا هندسه اقلیدسی صحیت می کنیم .
۱- هندسه اقلیدسی و پنج اصل اقلیدس
تاکنون در هندسه از اصولی استفاده می کردیم که اقلیدس آن ها را درحدود ۳۰۰ سال پیش از میلاد مسیح برای اولین بار در کتاب “اصول” خود جمع آوری کرده بود. از آن جائی که این اصول بدیهی به نظر می رسیدند، آن ها را بدون اثبات پذیرفت و سپس یر اساس این اصول قضایا را اثبات می کرد. لذا به این نوع هندسه، هندسه ی اقلیدسی گویند. پنج اصل مهم هندسه ی اقلیدسی عبارتند از:
۱- از هر دو نقطه ی مشخص فقط یک خط راست می گذرد.
۲- هر پاره خط رامی توان به میزان دلخواه امتداد داد.
۳- با هر نقطه و هر طولی می توان دایره ای به مرکز آن نقطه و به شعاع آن طو ل رسم کرد.
۴- همه ی زوایای قائمه با هم برابرند.
۵- از هر نقطه خارج یک خط فقط یک خط موازی با خط مذکور می توان رسم کرد.( این اصل که “اصل توازی” نام دارد، معادل با اصل پنجم اقلیدس است و در این جا به منظور درک بهتر، به جای اصل پنجم اقلیدس معادل آن ذکر شده است.
آیا در فضای اطرافمان که در آن زندگی می کنیم همه ی این اصول درست خواهد بود. آیا در هر سطحی با هر ویژگی، این اصول صادق خواهند بود؟

شکل شماره ۱ – تصویری از اقلیدس پدر علم هندسه
۲- هندسه غیر اقلیدسی
ریاضیدانان، سالیان درازی در طول تاریخ، تنها با هندسه ی اقلیدسی آشنا بودند تا این که در حدود ۲۰۰ سال پیش دریافتند، با تغییر کوچکی در اصول اقلیدس می توان انواع جدیدی از هندسه را معرفی کرد. همچنین ثابت کردند که هندسه های جدید، همانند هندسه ی اولیه (هندسه ی اقلیدسی) صحیح می باشند و با توجه به موقعیت و نوع فضا، باید از یکی از انواع هندسه استفاده کرد. یکی از این نوع هندسه های نااقلیدسی هندسه کروی می باشد .
قابل توجه است که تلاش دانشمندان ایرانی از جمله خواجه نصیر الدین طوسی، به ایجاد این شاخه از هندسه کمک زیادی کرده است.
یکی از قدیمی ترین شاخه های دانش ستاره شناسی, نجوم کروی است. با عنایت به اینکه گفتیم برای حل بسیاری از مسایل ستاره شناسی, می توانیم تمام اجرام سماوی را روی یک کره فرضی بنام کره سماوی در نظر بگیریم, اهمیت نجوم کروی در محاسبات, روشن تر می شود. همچنین چون ما روی کره ای به نام زمین زندگی می کنیم اهمیت هندسه کروی در جغرافیا نیز آشکار می شود .
بجز جغرافیا و نجوم هندسه کروی در بسیاری از علوم هم کاربرد گسترده دارد .
سابقه این رشته به ۴۰۰۰ سال پیش باز می گردد ولی هنوز در بسیاری از موارد نقش کلیدی را ایفا می کند.
۱) هندسه های نااقلیدسی :
در سده های بعد از این که اقلیدس اصول خود را وضع کرد بسیاری از ریاضی دان ها نتوانستند اصل پنجم را به عنوان اصل بپذیرند ( بیشتر عقیده داشتند این نمی تواند اصل بدیهی باشد و بیشتر به قضیه می ماند ) و تلاش کردند به کمک اصول دیگر این اصل را ثابت کنند ولی شکست خوردند و در واقع تلاش دانشمندان در اثبات اصل پنجم (به عنوان قضیه) از روی اصول دیگر منجر به تولد انواع هندسه نااقلیدسی شد .
( برای مطالعه اصل پنجم به کتاب “هندسه های اقلیدسی و نا اقلیدسی” تالیف گرینبرگ مراجعه کنید.)
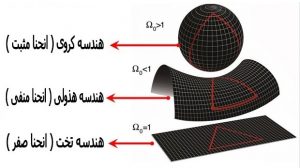
اساساً هندسه نااقلیدسی چیست؟ هر هندسه ای غیر از اقلیدسی را نااقلیدسی می نامند. از این گونه هندسه ها تا به حال زیاد شناخته شده است. اختلاف بین هندسه های نااقلیدسی و اقلیدسی تنها در اصل توازی است. در هندسه اقلیدسی به ازای هر خط و هر نقطه ناواقع بر آن یک خط می توان موازی با آن رسم کرد. نقیض این اصل را به دو صورت می توان در نظر گرفت. تعداد خطوط موازی که از یک نقطه نا واقع بر آن، می توان رسم کرد، بیش از یکی است و یا اصلاً خطوط موازی وجود ندارد .
۲) انواع هندسه نااقلیدسی:
هندسه های نااقلیدسی بسیارند که در اینجا فقط به بعضی از آنها اشاره می کنیم .
۲-۱)هندسه های هذلولوی :در این هندسه از هرنقطه خارج یک خط حداقل دو خط می توان به موازات آن رسم کرد .
۲-۲)هندسه های بیضوی : در این هندسه از هر نقطه خارج یک خط نمی توان خطی به موازات آن رسم کرد .
هندسه کروی هم حالت خاصی از هندسه بیضوی است و همه قوانین هندسه بیضوی در آن صادق است .
۳- اصول اقلیدس در هندسه کروی
ویژگی های یک سطح کروی با ویژگی های یک سطح تخت تفاوت دارد.
۱) تفاوت های یک سطح صاف و یک سطح کروی :
مفاهیم خط راست , نیم خط , پاره خط, فاصله دو نقطه از هم و… مفاهیم دیگر آنطور که در یک سطح تخت در نظر می گیریم با یک سطح کروی تفاوت دارد . در یک سطح تخت یک خط راست تا بینهایت امتداد دارد یعنی اگر شما در امتداد خط راست حرکت کنید دیگر هرگز به نقطه اول باز نمی گردید . در سطح کروی اگر در امتداد خط راست حرکت کنید بالاخره به جای اول خود برمی گردید . در یک سطح مسطح بر هر دو نقطه یک و تنها یک خط راست می گذرد در حالی که در یک سطح کروی می تواند بینهایت خط بگذرد ( نمونه آن نصف النهارها می باشند که از دو قطب شمال و جنوب می گذرند ) با تمام این وجود از ۵ اصل اقلیدس ۴ اصل در یک سطح صاف و یک سطح کروی مانند هم است تفاوت تنها در اصل پنجم است .
قبل از این که اصول اقلیدس را در مورد هندسه کروی بررسی کنیم چند اصطلاح را در مورد هندسه کروی بررسی می کنیم .
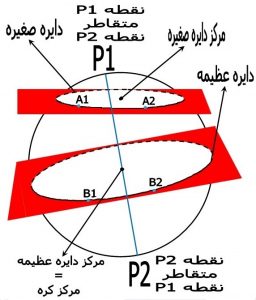
۲) دایره عظیمه و صغیره :
روی سطح یک کره می توان دوایر فرضی متعددی را در نظر گرفت. این دوایر به صورت نامحدود و با اندازه های مختلف قابل تصورند. به آن دسته از دوایری که مرکز آنها منطبق بر مرکز کره باشد, دایره عظیمه گفته می شود. پر واضح است از آنجا که شعاع دایره عظیمه مساوی شعاع کره است, محیط این دایره از تمام دوایر فرضی دیگر بزرگتر است و از اینرو نام آن را دایره عظیمه گذاشته اند. و در عوض دایره های دیگری که مرکز آنها بر مرکز کره منطبق نباشند دایره های صغیره نام گذاری می شوند ( شکل شماره ۱ )
دایره های صغیره و کبیره را به این صورت هم می توان تعریف کرد که اگر صفحه ای کره را قطع کند سطح مقطع کره با صفحه یک دایره خواهد بود .
در صورتی که صفحه از مرکز کره بگذرد دایره عظیمه تشکیل خواهد شد .
در صورتی که صفحه از مرکز کره نگذرد دایره صغیره تشکیل خواهد شد .
شکل شماره ۲ -دایره های صغیره و کبیره نقاط متقاطر و تعریف خط راست در هندسه کروی
۳) نقاط متقاطر :
در هندسه کروی هر دو نقطه که در امتداد قطر کره باشند نقاط متقاط نامیده می شوند و نقاطی که در امتداد قطر کره نباشند نقاط غیر متقاطر هستند . در شکل یک نقاط P1 وP2 نقاط متقاطر و نقاط A1وA2 ) همچنین نقاط B1وB2) نقاط غیر متقاطر هستند . ( شکل شماره ۲ )
۴) تعریف خط راست و اصل دوم اقلیدس :
طبق تعریف در هندسهٔ اقلیدسی، کوتاهترین مسیر بین دو نقطه را پاره خط می گویند و اگر از یک طرف تا بینهایت امتداد بدهتد نیم خط و اگر از دو طرف تا بینهایت امتداد بدهند خط راست می باشد . سایر مسیرها خطوط منحنی و شکسته می باشند و خط راست بحساب نمی آیند .
در هندسه کروی خط راست نداریم زیرا هر خطی خود یک دایره می باشد که اگر مرکز دایره منطبق با مرکز کره باشد دایره عظیمه در غیر این صورت دایره صغیره به حساب می آید ولی برای هماهنگی با هندسه مسطحه تعریف جدیدی از خط راست را در هندسه کروی ارائه دادند :
در هندسه کروی کوتاه ترین مسیر بین دو نقطه (که روی کره قرار دارد – اصولا وقتی از هندسه کروی صحبت می کنیم تمام نقاط و اشکال و خطوط و پاره خط ها و… روی سطح کره قرار دارند و خارج از سطح کره هیچ چیزی را در نظر نمی گیرند) را پاره خط و اگر از دو طرف امتداد بدهند یک خط نامیده می شود طول این خط در واقع بینهایت و نامحدود و باز نیست بلکه یک دایره عظیمه در روی کره است . (ثابت شده در یک سطح کروی کوتاهترین مسیر بین دو نقطه بر روی دایره عظیمه ای است که از آن دو نقطه می گذرد)
دایره های صغیره ای که در روی کره از دو نقطه می گذرند طبق تعریف خط راست بحساب نمی آیند و خط منحنی حساب می شوند زیرا انحنای آنها از انحنای کره بیشتر است . ( خط راست فقط و فقط در امتداد دایره عظیمه است )
در شکل شماره یک خط گذرنده از دو نقطه A1 وA2 خط راست نیست یک خط منحنی است . ولی خط گذرنده از دو نقطه B1وB2 یک خط راست می باشد .
بنابر این اصل دوم اقلیدس در هندسه کروی هم با هندسه مسطحه سازگار است با این تفاوت که در هندسه کروی اندازه خط نامحدود نیست بلکه محدود و برابر محیط کره است .
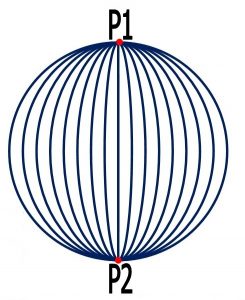
۵) اصل اول اقلیدس و تعداد خطوط گذرنده از دو نقطه :
طبق اصل اول اقلیدس از هر دو نقطه یک خط راست می گذرد در هندسه کروی اما مسئله فرق می کند و دو حالت وجود دارد :
۲-۱) در صورتی که دو نقطه غیر متقاطر باشند فقط یک خط راست ( دایره عظیمه ) می گذرد .
۲-۲ ) در صورتی که دو نقطه متقاطر باشند بینهایت خط راست می گذرد ( شکل شماره ۳)
شکل شماره۳ -بر دو نقطه متقاطر P1 و P2 بیشمار خط راست می گذرد
۶) اصول سوم و چهارم اقلیدس :
اصل سوم اقلیدس هم در این مورد صادق است به شرطی که حداکثر طولی را که می توان دایره را رسم کرد شعاع کره بگیریم ( در هندسه مسطحه هرجا صحبت از نامحدود یا بینهایت می شود در هندسه کروی به شعاع , قطر و محیط کره تعبیر می شود )
اصل چهارم اقلیدس هم در هندسه کروی برقرار است . زیرا در هندسه کروی هم می توان زاویه قائمه کشید و همه زاویه های قائمه هم برابرند .
۶) هندسه کروی و اصل پنجم اقلیدس :
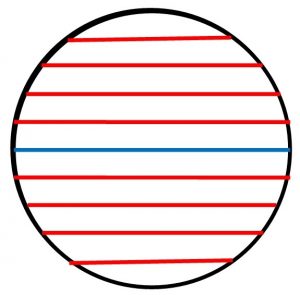
در هندسه کروی هرگاه صحبت از خط راست نامحدود باشد منظور یک دایره عظیمه است می توان ثابت کرد که هر دو دایره عظیمه ( که در هندسه کروی خط راست نامیده می شوند ) در روی کره دردو نقطه که روی قطر کره هستند و نقاط متقاطر نامیده می شوند (و در واقع بیشترین فاصله را از همدیگر دارند ) همدیگر را قطع می کنند بنابر این در هندسه کروی خطوط موازی نداریم . و این مهمترین تفاوت هندسه کروی و هندسه مسطحه می باشد .
نکته : بسیاری از اوقات مدارهای جغرافیائی را خطوط موازی می نامند زیرا صفحات آنها با هم موازیند ولی در هندسه کروی آنها را خط راست نمی نامیم زیرا انحنای آنها از انحنای کره بیشتر است . همچنان که در هندسه مسطحه کمان ها را خط راست نمی نامیم . ( شکل شماره ۴ )
شکل شماره ۴ – خطوطی که روی دایره عظیمه نباشند خط راست نیستند
۴- کاربرد هندسه کروی در مسیر حرکت هواپیماها و تعیین جهت قبله :
کوتاه ترین فاصله بین دو نقطه واقع بر روی یک کره, قوس دایره عظیمه ای است که از آن دو نقطه عبور می کند.
با توجه به این اصل در هندسه کروی, باید با دید جدیدتر و واقع بینانه تری به بعضی مسائل نگاه کنیم .
در شکل شماره ۴ نقطه A و B در یک مدار ( عرض جغرافیائی ) قرار دارند آنچه در نگاه اول به نظر می رسد این است که برای حرکت از نقطه A به نقطه B باید دقیقا رو به غرب برویم در این صورت از مسیری که با رنگ آبی نشان داده شده حرکت خواهیم کرد . ولی بنا بر اصل هندسه کروی نزدیکترین مسیر بین A و B بر روی دایره عظیمه ای است که از A و B می گذرد ( مسیر قرمز ) بنابر این باید ابتدا از نقطه A به سمت شمال غرب برویم و پس از طی مسافتی تعغیر جهت داده و به سمت جنوب غرب حرکت کرده تا به نقطه B برسیم در این صورت روی دایره عظیمه حرکت می کنیم . و نزدیکترین فاصله را طی کرده ایم .
به همین ترتیب وقتی صحبت از جهت نقطه A به سمت B می کنیم باید به جای غرب به شمال غرب اشاره کنیم . هر چند در وحله اول بنظر عجیب می آید ولی چون نزدیکترین فاصله A تا B روی مسیر قرمز است بنابر این جهت هم بر روی مسیر قرمز یعنی شمال غرب است نه غرب (شکل شماره ۵ )
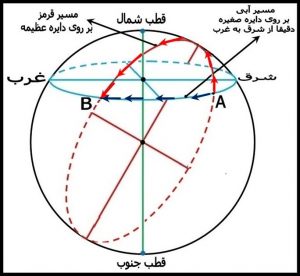
شکل شماره ۵ -کوتاهترین فاصله بین دو نقطه A و B که در یک مدار قراردارند.
این مسئله در تعیین قبله هم اهمیت دارد , فرض کنید نقطه B مکه باشد بنابر این جهت قبله در نقطه A به سمت شمال غرب می باشد نه به سمت غرب
شهر مکزیکو سیتی با مختصات (۱۹,۲۵N-100,52W) تقریبا با مکه در یک عرض جغرافیائی قرار دارد ( در غرب مکه ) ولی جهت قبله به جای این که در جهت شرق باشد به سمت شمال شرق است ( شکل شماره ۶ ) مختصات مکه (۲۱,۲۸N-39,58E)
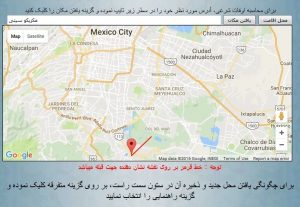
شکل شماره ۶ – جهت قبله در شهر مکزیکو سیتی بجای شرق به سمت شمال شرق می باشد
در هواپیمائی هم خلبانان و مسئولین هواپیمائی چون از این موضوع آگاه هستند برای صرفه جوئی در وقت و هزینه و مصرف بنزین بجای این که مستقیما به سمت غرب بروند ( مسیر آبی ) ابتدا به سمت شمال غرب رفته و بعد از طی مسیری تعغیر جهت داده به سمت جنوب غرب حرکت می کنند . ( مسیر قرمز )
البته مسیرهای هوائی از عوامل دیگری همچون امنتیت پرواز ( از روی کشورهائی که اجازه نمی دهند با خطرناکند پرواز نمی کنند ) آب و هوا و … هم پیروی می کنند .
شکل شماره ۷ مسیر پرواز تهران با مختصات (۳۵,۴۳-۵۱,۲۳E) و لس آنجلس(۳۴,۰۳N-118,15W) را نشان می دهد ( مسیر پرواز ۱۲۲۰۹ کیلومتر ) دیده می شود که بجای پرواز مستقیم یه سمت غرب ابتدا به سمت شمال غرب ( روسیه ) حرکت کرده و بعد در شمال گروئنلند تعغیر جهت داده و به سمت جنوب غرب ( کانادا ) حرکت کرده تا به مقصد برسد (در روی کره جغرافیائی می توانید با نخ دو مسیر را اندازه گرفته تا بفهمید کدام کوتاه تر است.) مسیر شرقی غربی(مسیر قرمز)یا مسیری که در نقشه آمده است .
البته اگر فاصله دو نقطه از هم کم بوده و یا به استوا نزیکتر باشند مسیر بیشتر به شرقی غربی نزدیک می شود تا در استوا نزدیک ترین مسیر همان مسیر شرقی غربی می شود.(مسیر قرمز ۱۵۴۷۵کیلومتر است)
فکر می کنید چگونه حساب شده است ؟
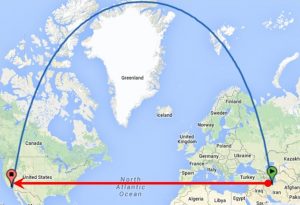
شکل شماره ۷ – مسیر پرواز از تهران به لس آنجلس دو شهر با عرض جغرافیائی تقریبا برابر
مسیر نشان داده شده با رنگ قرمز کوتاه ترین مسیر نیست . چون در امتداد دایره صغیره است مسیر آبی کوتاهترین مسیر است .
۵- دایره کروی و نسبت محیط دایره به قطر در هندسه کروی و مسطحه
۱) اندازه کمان و طول کمان در هندسه مسطحه و کروی
قبل از این که موضوع مثلث کروی را شروع کنیم راجع به پاره خط صحبت می کنیم . در هندسه مسطحه وقتی راجع به پاره خط صحبت می کنیم تنها طول پاره خط را در نظر می گیریم ولی وقتی راجع به کمان ها صحبت می کنیم هم اندازه کمان و هم طول کمان را در نظر می گیریم. اندازه کمان را همانند زاویه در نظر می گیرند یعنی اگر یک دور کامل دایره ۳۶۰ درجه باشد چون کمان همیشه قسمتی از یک دایره است پس بر حسب این که چه کسری از محیط دایره است بین ۰ تا ۳۶۰ در نظر می گیرند ( θ <= 180 ۰ =< ) بنابر این اندازه کمان برابر است با اندازه زاویه مرکزی مقابل به آن که با واحد های زاویه مانند درجه و گراد و رادیان اندازه گرفته می شود . ( شکل شماره ۸ )
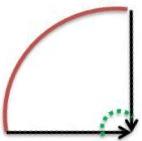
شکل شماره ۸ – اندازه کمان
ولی طول کمان عبارت است از فاصله بین دو سر کمان که بر حسب واحدهای طول(متر و سانتی متر وکیلومتر و… ) سنجیده می شود ( شکل شماره ۹ )

شکل شماره ۹ – طول کمان
رابطه بین اندازه کمان و طول کمان عبارت است :
اندازه کمان (بر حسب رادیان) ضربدر طول کمات یعنی : L=θ×r و اگر بر حسب درجه بیان کنیم می شود : L=θ×r =(π/ ۱۸۰)×r که در آن r شعاع دایره است . ( شکل شماره ۱۰ )
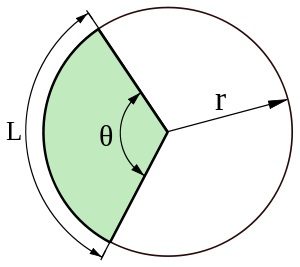
شکل شماره ۱۰ – رابطه بین اندازه کمان و طول کمان
در هندسه کروی تمام خطوط مستقیم در واقع کمان هائی از دایره عظیمه کره هستند بنابر این علاوه بر طول کمان اندازه کمان طول هم دارند همانند هندسه مسطحه طول کمان بر حسب واحدهای طول و اندازه کمان بر حسب واحدهای زاویه است . و طبق همان فرمول های هندسه مسطحه بدست می آید .
۲) نسبت محیط دایره به قطر آن در هندسه مسطحه و کروی
در هندسه مسطحه نسبت محیط دایره به قطر آن برابر مقدار ثابتی است که آن را عدد پی (π ) می نامیم ( مقدار آن تقریبا برابر است با ۳٫۱۴۱۵۹۲) این در مورد همه دایره ها چه بزرگ چه کوچک بر قرار است . حال همین را در هندسه کروی بررسی می کنیم :
۳-۱) طبق اصل سوم اقلیدس با هر نقطه و هر طولی می توان دایره ای به مرکز آن نقطه و به شعاع آن طول رسم کرد.
در هندسه کروی هم همچنین است ولی طبق آنچه گفته شد در هندسه کروی:
اولا : همه نقاط و خطوط (تمام خطوط راست دایره های عظیمه هستند ) و پاره خط ها و… در روی کره هستند و بیرون کره هیچ چیزی نداریم .
ثانیا : در هندسه کروی منظور از نامحدود و دلخواه حداکثر به اندازه محیط دایره عظیمه هست (همچنان که دو خط راست همدیگر را در دو نقطه متقاط قطع کرده و خطوط موازی نداریم ) و بزرگتر از ان نداریم .
ثالثا : منظور از قطر دایره پاره خطی است که از مرکز دایره گذشته و دو نقطه دایره را بهم وصل کند و در هندسه کروی این پاره خط روی سطح کره است و قسمتی از دایره عظیمه می باشد بنابر این نباید با خطی که از داخل کره می گذرد و دو قسمت دایره را بهم وصل می کند اشتباه کند اشتباه کرد ( شکل شماره ۱۱ )
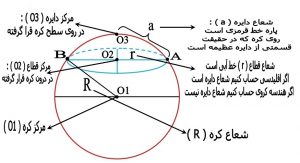
شکل شماره ۱۱ – دایره کروی : مرکز آن روی کره و قطر آن پاره خط AO3B می باشد که در روی کره قرار داردو به رنگ قرمز است
در این حالت نسبت محیط دایره به قطر آن را از دو راه می توانیم حساب کنیم :
۱) مرکز دایره را نقطه O2 در نظر گرفته و شعاع آن را r و قطر آن را پاره خط BO2A که در واقع به روش هندسه اقلیدسی عمل کرده ( کره را سه بعدی در نظر گرفته و مرکز دایره را مرکز قطاع در نظر می گیریم )
۲) مرکز دایره را نقطه O3 در نظر گرفته و شعاع ان را a و قطر ان را پاره خط که BO3A که در واقع به روش هندسه کروی عمل می کنیم .
این روابط را داریم :
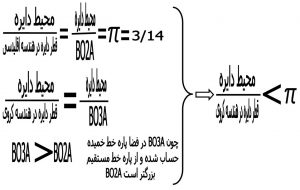
بنابر این در هندسه اقلیدسی نسبت محیط دایره به قطر آن برابر عدد π می باشد در حالی که در هندسه کروی کوچکتر از π می باشد ( در واقع در هندسه بیضوی که کروی حالت خاص ان است کوچکتر از π می باشد و در هندسه هذولی بزرگتر از π می باشد )
۶- خلاصه تفاوت هندسه اقلیدسی و بیضوی و کروی و هذولی
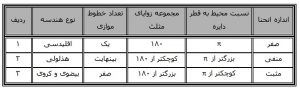
در جدول شماره یک تفاوت سه نوع هندسه در تعداد خطوط موازی که از یک نقطه خارج خط می توان رسم کرد و نسبت محیط دایره به قطر آن آورده شده است . ( شکل شماره ۱۲ )
![]()
شکل شماره ۱۲ – انحنای انواع هندسه و نسبت محیط دایره به قطر آن
جدول شماره ۱ – تفاوت سه نوع هندسه
ما بر روی زمین کروی زندگی می کنیم و برای رفتن از یک نقطه به نقطه ای دیگر باید روی یک کره حرکت کنیم (مگر آن که تونلی از داخل کره زمین حفر کرده و دو نقطه را بهم پیوند دهیم که فعلا ممکن نیست ) هر چه روی سطح به ظاهر مسطح زمین رسم کنیم در حقیقت روی یک کره رسم کرده ایم و همه روابط بر روی سطح یک کره است .
با این وجود زمین نسبت به ما بسیار عظیم و بزرگ است و وقتی روی آن زندگی می کنیم سطح آن را صاف و مسطح می بینیم .
در صورتی که بخواهیم نقشه یک ساختمان را رسم کرده و اجرا کنیم می توانیم زمین را تخت در نظر بگیریم اگر نقشه یک ناحیه و یا کشور کوچک را بخواهیم رسم کنیم باز هم نیاز چندانی به هندسه کروی نداریم . بنابر این بیجا نبود که انسان ها تا هزاران سال متوجه کروی بودن زمین نشدند . از این رو بود که مهندسان و نقشه برداران دنیای قدیم هرگز به هندسه کروی احتیاجی پیدا نکردند و از همان روابط هندسه اقلیدسی استفاده می کردند .
حال اگر بخواهیم نقشه را دقت بسیار بالا و یا نقشه یک کشور بزرگ و یا کل جهان را رسم کنیم و یا بخواهیم فاصله های بسیار زیاد را با وسیله ای مانند هواپیما برویم . دیگر باید از هندسه کروی استفاده کنیم .
۷- چگونه هندسه کروی به هندسه تخت تبدیل می شود ؟
ابتدا بیائیم مروری برکل تفاوت دو هندسه داسته باشیم :
۶-۱)درهندسه کروی خطوط راست دایره های عظیمه هستند پس اندازه بزرگترین خط برابر محیط دایره عظیمه است .
در هندسه مسطحه بزرگترین خط بینهایت است .
۶-۲) اگر یک نقطه خارج از خط داشته باشیم : در هندسه مسطحه می توانیم تنها یک خط رسم کنیم که خط مزبور را در فاصله بینهایت (ازنقطه) قطع کند(موازی باشد) در هندسه کروی اگر چه نمی توانیم خطی رسم کنیم که خط مزبور را قطع نکند ( موازی باشد ) ولی می توانیم خط مزبور را به گونه ای رسم کنیم که در فاصله ای حداکثر برابر یک چهارم محیط کره قطع کند. ( از دو طرف در دو نقطه متقاطر ) در این صورت تنها یک خط چنین خاصیتی دارد .
۶-۳) درهندسه کروی نسبت محیط دایره به قطر آن از عددπ کوچکتر است ولی هرچه دایره ای که رسم کردیم نسبت به محیط کره کوچکتر باشد به عدد π نزدیکتر می شود .
۶-۴) اندازه پاره خط ها در هندسه مسطحه برابر صفر درجه است (زیرا انحنا ندارد) ولی در هندسه کروی چون قسمتی از کمان دایره است اندازه هم دارد ( که بر حسب واحدهای درجه بیان می شود) ولی هرچه کره بزرگتر باشد (با ثابت نگه داشتن طول پاره خط) اندازه پاره خط ها کوچکتر می شود .
از تمام این مثال ها یک نتیجه را می شود گرفت و آن این که هرچه کره بزرگتر باشد روابط هندسی بیشتر به هندسه تخت و اقلیدسی نزدیک می شود و اگر شعاع کره بینهایت شود کره تخت شده و هندسه کره دقیقا مانند هندسه تخت می شود . اگر فاصله نقاط متقاطر بینهایت شود می توانیم بگوئیم خطوط موازی هم یکدیگر را در دو نقطه متقاطر قطع می کنند .
اگر هم کره به اندازه کافی بزرگ باشد باز هم ما نمی توانیم براحتی پی ببریم خطوط موازی در واقع موازی نیستند و در دو سوی کره همدیگر را قطع می کند .حتی در فضای تخت اگر در فاصله نسبتا دوری همدیگر را قطع کنند از نظر فیزیکی موازی در نظر گرفته می شوند .
۸- فضای کروی
می توانیم کره را یک جسم سه بعدی در فضای اقلیدسی در نظر گرفته و اختلاف بین سطح کروی و سطح مسطح را اختلاف بین فضای دو بعدی و سه بعدی در هندسه اقلیدسی بنامیم . ولی مسئله واقعا این نیست و لازم است هندسه جداگانه ای برای این جور سطوح در نظر بگیریم . از طرف دیگر فرض در نظر گرفتن هندسه ای مانند هندسه کروی این است که به داخل کره دسترسی نداشته باشیم پس همه چیز : دایره هائی که رسم می کنیم تا مثلث ها و چهار ضلعی ها همه در روی کره هستند که با روی سطح مسطح تفاوت دارند .
حال مسئله را کمی جلوتر ببریم فضای سه بعدی را در نظر می گیریم و در فضای سه بعدی دیگر دو خط دو حالت متقاطع و موازی ندارند بلکه حالت سومی به نام متنافر هم وجود دارد در فضای سه بعدی تقاطع و توازی صفحه ها را داریم و اشکال سه بعدی همچون مکعب و هرم و کره و… این هندسه و فضای سه بعدی هم هندسه اقلیدسی است حال دید خود را وسیعتر کنیم و بپرسیم آیا می شود فضای سه بعدی ما هم هندسه ای مثلا کروی داشته باشد حتما می پرسید یعنی چه ؟ یک مثال می زنیم :
اگر در روی کره زمین در یک جهت مشخص حرکت کرده (مثلا ابتدا پیاده )و مرتب به یک جهت برویم بعد از مدتی(مثلا چندین سال) به همان جائی که حرکت کردیم برمی گردیم و شاید تعجب هم بکنیم ولی راحت توجیه می شویم و می توانیم علت آن را درک کنیم . حال با وسیله نقلیه ای که سرعت بیشتری دارد زودتر به جای اولمان برمی گردیم و…. حال فرض کنیم زمین ما بزرگتر از اینی باشد که هست دیرتر به نقطه اول می رسیم و اگر باز هم بزرگتر دیرتر و… و اگر بی نهایت بزرگ باشد هرگز بر نمی گردیم .
حال این سوال را در فضای سه بعدی مطرح می کنیم اگر بگویند همانند زمین در فضا هم اگر رو به یک جهت برویم به جای اولمان برمی گردیم چه می گوئید ؟ حتما می گوئید این دیگر امکان ندارد چون این مسئله را نمی توانیم با عقل سلیم توجیه کنیم و درک کنیم درک این مسئله نیازمند درک مفهوم بعدهای بالاتر از سه بعد است و ما موجودات سه بعدی نمی توانیم با عقل سلیم این مسئله را تجسم کنیم ولی کیهان برای این ساخته نشده تا ما ان را درک کنیم احتمال این که هندسه جهان اقلیدسی نباشد و فضا حالتی همانند فضای کروی یا هذولی و یا … باشد هم وجود دارد ولی ممکن است انحنای فضا بقدری بزرگ باشد که نتوانیم اندازه بگیریم و….
ممکن است در فضا از یک طرف حرکت کرده دو باره به نقطه اولمان برگردیم ولی اگر با سریعترین وسیله و با سرعت نور هم حرکت کنیم و عمرمان هم کفاف بدهد مدت زمان برگشتن به نقطه اول از عمر جهان هم بیشتر باشد با این حال فضا می تواند غیر تخت باشد هم اکنون دانشمندان به تخت بودن فضا هم شک دارند و می گویند شاید هندسه جهان گونه ای دیگر باشد و ما هنورز نتوانستیم آن را اندازه بگیریم .
نکته دیگر این که مفهوم فضاهای چند بعدی شاید از نظر فیزیکی غیر ممکن باشد ولی از نظر ریاضی غیر ممکن نیست کافی است روابط را گسترش داده و محورها را اضافه کنیم .
![]()
برای مطالعه سایر مقاله های ریاضی اینجا را کلیک کنید .
![]()
برای مطالعه مقاله های روانشناسی اینجا را کلیک کنید .
![]()
برای دیدن زیباترین آلبوم های طبیعت روی شکل زیر کلیک کنید
![]()
برای آموزش کامل و حرفه ای گوگل مپ روی شکل زیر کلیک کنید
![]()
۱) هر گونه اظهار نظر را در فرم اظهار نظر کاربران وارد کنید .
۲) نظرات بعد از تایید مدیریت نشان داده می شود .
۳) با انتقادات و پیشنهادات سازنده خود ما را هرچه بیشتر همراهی کنید . مدیریت از انتقادات و پیشنهادات سازنده شما استقبال میکند .
۴) نوشته های قرمز پر رنگ ارجاع به لینک هستند که هنوز لینک آنها قرار داده نشده است ( هنوز صفحه آنها منتشر نشده است )
۵) نوشته های آبی پر رنگ ارجاع به لینک هستند که لینک آنها قرار داده شده است ( صفحه آنها منتشر شده است )
۶) هرگونه بهره برداری : کپی تمام و یا قسمتی از مطالب این سایت بدون ارجاع منبع آن ممنوع می باشد .
۷) تکثیر فایل های Pdf با ذکر منبع آزاد ولی فروش آن تحت هر عنوان و با ذکر منبع هم ممنوع می باشد.
![]()



سلام
چه منابعی رو برای یادگیری هندسه کروی پیشنهاد می کنید؟