مکانیک مداری یا اخترپویاشناسی( astrodynamics) شاخهای از علم مکانیک است که به حرکت اجرام آسمانی (کهکشان ها تا ستارگان و سیارات و قمرها و…) و مدارهائی که بر اثر گرانش متقابل یکدیگر تشکیل می دهند می پردازد. حرکت اجرام سماوی بر اساس قانون جاذبه عمومی نیوتن و همچنین قوانین کپلر(که بر گرفته از همان قانون گرانش جهانی است )می باشد . در مقاله “مکانیک مداری و قوانین کپلر(۱)“ در مورد مکانیک مداری و قوانین کپلر توضیح داده و قوانین کپلر را ثابت کردیم در این مقاله در مورد کاربرد قوانین کپلر و انواع مدارها توضیح می دهیم . برای دسترسی به کل لینک های مقاله به “جمع بندی مقاله های فصل هفتم – گرانش(۱) “مراجعه کرده و طبق راهنمائی روی لینک های آبی کلیک کنید.
۱-مختصری از گرانش
قبل از توضیح در موردحرکات مداری بهتر است در مورد گرانش و قانون جاذبه عمومی توضیحات مختصری بدهیم برای توضیحات کاملتر به لینک مقاله هائی که گذاشتیم(با رنگ آبی)مراجعه کنید.بخصوص مقاله “ قانون جاذبه عمومی نیوتن“ را حتما مطالعه کنید.
۱) تاریخچه گرانش قبل از نیوتن
از دوران باستان برای بشر همواره سوال بود که چرا همه اشیا روی زمین سقوط می کنند ولی ماه و خورشید و ستارگان روی زمین سقوط نمی کنند؟ همچنین حرگت هماهنگ همه ستارگان از شرق به غرب برای آنها یک معما بود . براین اساس بطلمیوس دانشمندیونانی (۹۰–۱۶۸ میلادی) نجوم بطلمیوسی را پایه گذاری کرد که بر اساس آن تمام ستارگان به کره ای به نام کره آسمان چسبیده اندو این کره (که مرکز آن زمین است)گرد زمین می چرخد. ۱۵۰۰سال طول کشیدتا کپرنیک منجم لهستانی(۱۴۷۳تا ۱۵۴۳) توانست بطلان آن را نشان دهد که کره آسمان وجود ندارد و طلوع و غروب و حرکت اجرام آسمانی نتیجه چرخش زمین است و همه سیارات ازجمله زمین به دورخورشید می چرخند. برای مطالعه کامل به مقاله “تاریخچه گرانش “مراجعه کنید .
۲) زندگینامه نیوتن
سِر ایزاک نیوتن در ۲۵دسامبر۱۶۴۲ انگلیس بدنیا آمد.در ۱۸سالگی یعنی در سال۱۶۶۱وارد کالج ترینیتی شد و مراحل ترقی را یکی پس ازدیگری طی کرد.نیوتن نتیجه کشفیات خودش را (در مورد قوانین حرکت و قانون جاذبه عمومی)در سال۱۶۸۷در کتابی به نام “ اصول ریاضی فلسفه طبیعت “منتشر کرد و نام خود را جاودانه کرد . برای توضیح کامل زندگینامه نیوتن به مقاله “ زندگینامه نیوتن “ مراجعه کنید .
۳) نیوتن و گرانش
در مقاله “نیوتن و گرانش“داستان کشف و فرمول بندی نیروی گرانش جهانی را توسط نیوتن شرح می دهیم. از داستان اقتادن سیب شروع کرده تا مقایسه نیروی جاذبه زمین در مدار ماه و…همچنین داستان چرخش سطل های آب و…که منجر به کشف گرانش شد.
۴) قانون جاذبه عمومی نیوتن
در مقاله “قانون جاذبه عمومی نیوتن“ ابتدا فرمول قانون گرانش جهانی را شرح داده و بسیاری از پدیده های مربوط به آن را توضیح داده و بعد از محاسبه ثابت گرانش جرم زمین و خورشید را محاسبه می کنیم .
۲- مختصری از مکانیک مداری یک
مکانیک مداری شاخهای از علم مکانیک است که به حرکت اجرام آسمانی و مدارهائی که بر اثر گرانش متقابل یکدیگر تشکیل می دهند می پردازد . درمقاله “مکانیک مداری و قوانین کپلر(۱)“ در مورد مکانیک مداری ، قوانین کپلر و اثبات این قوانین توضیح دادیم آنچه در این بخش توضیح می دهیم در واقع خلاصه مطالبی است که در این مقاله گفته شده است بنابر این قبل از مطالعه مقاله حاضر مقاله “مکانیک مداری و قوانین کپلر(۱)“ را حتما مطالعه کنید .
۱) مکانیک مداری و مقاطع مخروطی
مدارهای اجرام آسمانی یکی از مقاطع مخروطی می باشند. مقاطع مخروطی شکل هائی می باشند که از برخورد یک صفحه با یک مخروط دوار بدست می آیند(برای مطالعه درمورد مقاطع مخروطی به مقاله “مقاطع مخروطی “ مراجعه کنید) از این رو مطالعه مقاطع مخروطی و معادله آنها درمکانیک مداری بسیار مهم میباشد.
۲) توپ نیوتن
نیوتن در کتاب اصول خود توپ بسیار بزرگ و پرقدرت را ذکر کرده که بالای یک کوه بلند برده و لوله آن را به صورت افقی (موازی با سطح زمین) گرفته و اقدام به شلیک می کنیم. (ازمقاومت هوا صرف نظر می کنیم) اگر سرعت پرتاب گلوله کم باشد توپ در نزدیکی دامنه کوه سقوط می کند اگر سرعت گلوله بیشتر باشد توپ مسیر بیشتری را قبل از سقوط طی می کند سرانجام اگر سرعت گلوله به حدود ۸کیلومتر درثانیه برسد گلوله درمدار دایره ای برگرد زمین می چرخد و اگر بیشتر از ۸ و کمتر از ۱۱/۲کیلومتر در ثانیه باشد در مدار بیضی و اگر۱۱/۲ کیلومتر درثانیه و بیشتر باشدگلوله در مدارسهمی و هذولی برای همیشه ازجاذبه زمین فرار می کند.
از این رو مطالعه مقاطع مخروطی (دایره ، بیضی ، سهمی و هذولی)درمکانیک مداری بسیار مهم می باشد.
۳) سرعت مداری
بدین گونه جسمی که ازیک ارتفاع به صورت افقی شلیک شود اگرسرعت کافی داشته باشد بر روی زمین(یا هر سیاره و جرم عظیم دیگر)سقوط نمی کند بسته به سرعتی که دارد یا بر روی مداردایره ای یا بر روی مدار بیضی به دور زمین گردش می کند.سرعتی که پرتابه با آن به دور زمین می چرخد را سرعت مداری می نامند این سرعت مدارپرتابه را مشخص می کند.در صورتی که مدار دایره کامل باشد این سرعت به حداقل می رسد و هرچه مدار بیضی تر و هرچه بیضی کشیده تر باشد این سرعت بیشتر می شود.
بنابراین «حداقل سرعت مداری »در یک ارتفاع به حداقل سرعتی می گویند که برای نگه داشتن یک قمر( ماهواره ،سیاره و…) به دور سیاره مادردر آن ارتفاع لازم است و همانطور که گفته شداین مدار باید دایره کامل باشد . هر چه ارتفاع بیشتر باشد حداقل سرعت مداری نیز بیشتر می شود .
۴) سرعت در مدارهای بیضی و دایره
ماهواره و قمری که دور یک سیاره می چرخد می تواند مداری دایره ای یا بیضی داشته باشد در مدار دایره ای سرعت قمر همواره ثابت است و سرعت متوسط با سرعت لحظه ای برابر است ولی در مدارهای بیضی فاصله قمر از سیاره مادر تغییر می کند بنابراین سرعت متوسط و لحظه ای مساوی نمی باشد .
اگر سرعت ماکزیمم را در نظر بگیریم در مدار بیضی این سرعت از مدار دایره بیشتر می باشد ولی اگر سرعت متوسط را حساب کنیم این سرعت کمتر می باشد .
۵) سرعت مداری در سطح سیاره
اگر سطح سیاره صاف و یکدست بوده و هیچگونه جوی نداشته باشد قمری که همسطح سیاره به دور آن دوران می کند بیشترین سرعت مداری را نسبت به قمرهای دیگر دارد.در این حالت فاصله قمر از سطح سیاره برابر شعاع سیاره میشود بنابر این می توانیم دوره تناوب و سرعت را بر حسب شعاع سیاره حساب کنیم ولی اگر دوره تناوب را بر حسب چگالی سیاره حساب کنیم می بینیم که دوره تناوب حتی به شعاع سیاره هم بستگی نداشته و فقط به چگالی سیاره بستگی دارد .
۶) کپلر و قوانین او
یوهانس کپلر(Johannes Kepler)در ۲۷دسامبر۱۵۷۱درشهر وایلدراشتات آلمان بدنیا آمد . او دانشمند، ریاضیدان و ستارهشناس مشهوری بود.کپلر با استفاده از رصدهای تیکو براهه (ستاره شناس مشهور دانمارکی)و مطالعه بر روی رصدها و جداول نجومی او ، همچنین رصدهائی که خودش (بخصوص بر روی مریخ ) انجام داد به این نتیجه رسید که بر خلاف آنچه کپرنیک و منجمان دیگر نظر داده اند مدار سیارات به دور خورشید به جای دایره بیضی می باشد بعدها او دو قانون مشهور دیگر را هم کشف کرد که جمعا قوانین سه گانه کپلر نامیده شدند که در ادامه به آنها خواهیم پرداخت .
۷) قوانین کپلر
اولین قانون کپلر در کتاب “نجوم جدید” در سال ۱۶۰۶منتشر شد و تا سال ۱۶۱۸دو قانون دیگر هم منتشر شد
خلاصه قوانین کپلر به این صورت می باشد :
قانون اول کپلر(قانون بیضوی ها ) : « مدارحرکت سیارات به گرد خورشید یک بیضی است که خورشید در یکی از دو کانون آن قرار دارد. »
قانون دوم کپلر(مسطح معادل) : «خط وصلکننده هر سیاره به خورشید در زمانهای مساوی مساحت های مساوی جاروب میکند.»
قانون سوم کپلر(قانون هارمونیک) : «نسبت مکعب فاصله متوسط هر سیاره تا خورشید با مربع زمان یک دور کامل گردش سیاره تناسب مستقیم دارد. »
۸) اثبات قوانین کپلر
کپلر بر پایه رصدهای نجومی توانست به این سه قانون دست پیدا کند ولی نتوانست آن ها را ثابت کند ولی توانست یک حرکتی را بین دانشمندان برای توجیه این قوانین پیدا کند و سرانجام نیوتن با کشف قانون جاذبه عمومی توانست قوانین کپلر را هم اثبات کند.درمقاله “مکانیک مداری و قوانین کپلر(۱)“ قوانین سه گانه کپلر را اثبات کردیم . قوانین کپلر دنیای نجوم را دگرگون کرد و راهی جدید به شناخت جهان باز کرد .
۹) معادله بنیادین مکانیک مداری
طبق قانون سوم کپلر نسبت مکعب فاصله یک سیاره از خورشید به مربع دوره تناوب آن مقداری ثابت بوده و به فاصله و جرم سیاره و… بستگی ندارد و تنها به خورشید(یا هر سیاره مادر دیگر) بستگی دارد این قانون که با فرمول
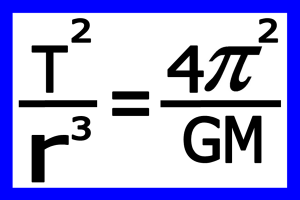
بیان می شود یکی از مهمترین فرمول ها در مکانیک مداری می باشد که در ادامه خواهیم دید همین فرمول چه کاربردی دارد و چه داده هائی را می توان از همین فرمول در آورد.(محاسبه جرم خورشید و سیاره ها و فاصله سیاره ها ازخورشید و… )
۳- کاربرد قانون سوم کپلر
قانون سوم کپلر استفاده های گسترده ای در نجوم و فضانوردی و… دارد . از اندازه گیری مدارهای سیاره ها تا تعین جرم آنها و تعین جرم ستاره های دوتائی و… جرم کلی کهکشان و… تا فضانوردی
در این بخش در مورد کاربردهای مختلف قانون سوم کپلر توضیح می دهیم .
۱) قانون سوم کپلر و منظومه شمسی
همچنان که معادله بنیادی حاصل ازقانون سوم کپلرنشان می دهد می توان این معادله را به سامانه خورشیدی تعمیم داد کافی است در معادله فوق به جای Mجرم خورشید(Ms) را قرار می دهیم . (همچنین در این معادله r فاصله از خورشید و T دوره تناوب سیاره می باشد ) بنابر این داریم :
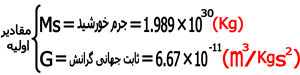
با جاگذاری مقادیر اولیه در معادله بنیادی قانون سوم کپلر در مورد خورشید به این نتیجه می رسیم :

حال با جا گذاری مقادیر ثابت ، مقدار عددی ثابت T2/r3را درمورد منظومه خورشیدی بدست می آوریم . در مورد کاربرد این معادله در منظومه شمسی در قسمت های بعد مفصل توضیح می دهیم .

۲) اندازه گیری دوره تناوب
با استفاده از فرمول قانون سوم کپلر براحتی می توان دوره تناوب یک قمر را که دور سیاره مادر می چرخد محاسبه کرد (دریک مجموعه مداری جسم عظیم مرکزی را سیاره مادر و جسمی کوچکی که دور جسم بزرگتر می چرخد را قمر می نامیم) برای این کار داریم( r فاصله مرکز قمر از مرکز سیاره و M جرم سیاره مادر) :
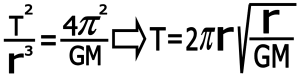
بنابراین دوره تناوب از این فرمول بدست می آید:

در صورتی که این معادله را بخواهیم در مورد دوره تناوب سیاره ها به کار ببریم r فاصله مرکز سیاره ازمرکز خورشید (در مدارهای بیضی نیم قطر بزرگ بیضی)،T دوره تناوب سیاره و M هم جرم خورشید می باشد .
۳) محاسبه سرعت
برای اندازه گیری سرعت ابتدا مدارها را دایره در نظر می گیریم . در مدارهای دایره سرعت و فاصله قمر از سیاره مادر ثابت می باشد بنابر این می توانیم بنویسیم :
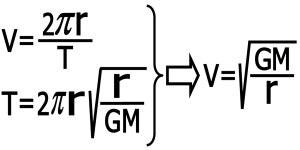
بنابراین سرعت از این فرمول بدست می آید:

فرمولی که برای سرعت بدست آوردیم مربوط به مدارهای دایره ای می باشد . در این مدارها سرعت ثابت است و بنابراین سرعت متوسط و سرعت لحظه ای یکسان است در صورتی که مدارها بیضوی باشد سرعت قمر دیگر ثابت نیست ولی می توانیم با این فرمول سرعت متوسط را بدست بیاوریم در این صورت به جای r باید نیم قطر بزرگ بیضی را قرار دهیم و برای سرعت لحظه ای به جای r فاصله لحظه ای قمر را از سیاره مادر در نظر بگیریم و فاصله لحظه ای را هم می توانیم از قانون دوم کپلر استخراج کرده که در اینجا دیگر در مورد آن توضیح نمی دهیم برای منظومه خورشیدی به جای M جرم خورشید را قرار می دهیم .
۴) محاسبه فاصله زمین از خورشید
اندازه گیری فاصله زمین تا خورشید سنگ بنای اندازه گیری فاصله ها در منظومه شمسی و کیهان می باشد. برای اندازه گیری فاصله زمین تا خورشید ازگذر زهره ازروی خورشید استفاده میکنندو درقسمتی از محاسبات باید از قانون سوم کپلر استفاده کرد در مقاله “ فاصله زمین تا خورشید “ در این باره بیشتر توضیح میدهیم .
۵) اندازه گیری جرم خورشید
به کمک قانون سوم کپر و با داشتن دوره تناوب زمین(یک سال زمینی که از هزاران سال پیش مشخص شده بود)و فاصله زمین از خورشیدجرم خورشید براحتی محاسبه می شود . در مقاله “قانون جاذبه عمومی نیوتن” ( بخش هفتم)در این باره توضیح دادیم .
۶) محاسبه فاصله سیاره ها
دوره تناوب سیارات براحتی با رصدهای نجومی از روی زمین مشخص می شود(در مقاله های آینده در این مورد توضیح می دهیم) با استفاده از قانون سوم کپلر و مشخص بودن جرم خورشید براحتی می توان فاصله سیاره ها را از خورشید بدست آورد .
۷) اندازه گیری جرم سیاره ها و سامانه های مداری
برای اندازه گیری جرم یک سیاره کافی است فاصله سیاره از زمین و دوره تناوب یکی از اقمار سیاره مشخص شود همچنین با دانستن فاصله سیاره از زمین فاصله قمر از سیاره هم براحتی مشخص می شود در این صورت با استفاده از قانون سوم کپلر می توان جرم سیاره را تعیین کرد . در دوران اخیر که کاوشگرهای متعددی به سیارات منظومه شمسی فرستاده شده است با قرار دادن کاوشگرها در مدار سیارات با دقت بسیار بیشتری می توان جرم سیارات را اندازه گیری کرد .
۸) اندازه گیری جرم ستارگان دوتائی
بسیاری از ستارگان کهکشان ستارگان دوتائی هستند در ستارگان دوتائی با مشخص بودن فاصله ستارگان از زمین (در مورد اندازه گیری فاصله ستارگان در مقاله های آبنده توضیح می دهیم ) و اندازه گیری دوره تناوب و فاصله دو ستاره از مرکز جرم مشترکشان ( که آن هم با دانستن فاصله مجموعه از زمین براحتی محاسبه می شود ) می توان جرم تک تک ستارگان مجموعه را بدست آورد .
۹) قانون سوم کپلر در مورد زمین
حال می خواهیم این فرمول ها را در مورد زمین محاسبه کنیم اگر در فرمول فانون سوم کپلر به جای M جرم زمین(Me) را قرار داده و محاسبات عددی مربوط به آن را انجام دهیم داریم :
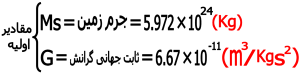
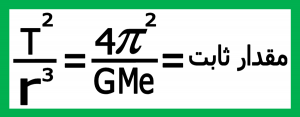
با جاگذاری مقادیر عددی در معادله فوق به این نتیجه می رسیم .

۴- حرکت در سطح سیاره
در این بخش مسئله ای خاص را در نظر می گیریم فرض کنیم سطح زمین (یا هر سیاره مادر دیگر) عاری از جو و هرگونه پستی و بلندی بود و ما یک ماهواره (یا قمر) را تقریبا در سطح زمین(ارتفاع صفر کیلومتر)قرار می دادیم. می خواهیم دوره تناوب و سرعت این ماهواره را بدست بیاوریم . با توجه به فرمول هائی که از قانون سوم کپلر بدست آوردیم براحتی می توانیم به جای r مقدار Ry (شعاع سیاره y) را قرار دهیم .
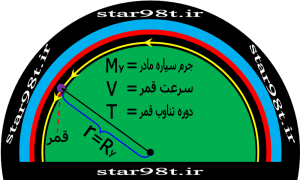
شکل شماره ۱ – سرعت مداری در سطح
۱)مقادیر اولیه
ابتدا مقادیر اولیه را می نویسیم :
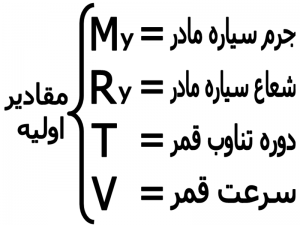
۲) محاسبه دوره تناوب و سرعت بر حسب شعاع سیاره مادر
دوره تناوب یک قمر را که به دور سیاره مادر می چرخد حساب کردیم . کافی است در فرمول محاسبه شده به جای r شعاع سیاره را قرار دهیم بنابر این داریم :
۲-۱) دوره تناوب : دوره تناوب به این صورت بدست می آید .

۲-۲) سرعت : سرعت این قمر هم به این صورت بدست می آید .

۳) محاسبه دوره تناوب و سرعت بر حسب چگالی
اگر به جای My فرمول سرعت و دوره تناوب را بر حسب چگالی حساب کنیم نتایج شگفت آوری می گیریم .
برای این کار ابتدا My را برحسب چگالی حساب کرده تا در معادلات حذف شود بنابر این داریم .
۳-۱) محاسبه My بر حسب چگالی :
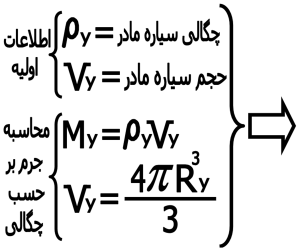
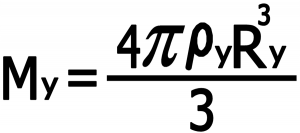
۳-۲) محاسبه دوره تناوب : دوره تناوب به این صورت بدست می آید
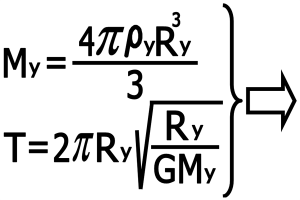
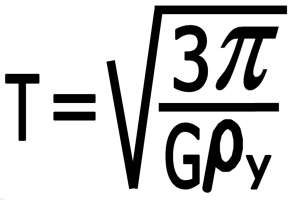
بنابر این دوره تناوب قمر بر حسب چگالی و شعاع قمر به این صورت محاسبه می شود :
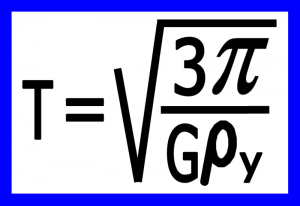
۳-۳) محاسبه سرعت : سرعت به این صورت بدست می آید
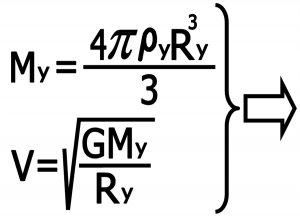
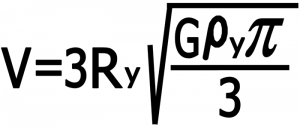
بنابر این سرعت قمر بر حسب چگالی و شعاع قمر به این صورت محاسبه می شود :
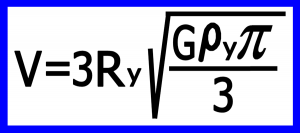
۴) دوره تناوب و اندازه قمر به چه بستگی دارد ؟
همچنان که از فرمول ها مشاهده می شود دوره تناوب به جرم و شعاع سیاره بستگی ندارد بلکه فقط به چگالی سیاره بستگی دارد این به آن معنی است که اگربه جای زمین هرسیاره دیگری باهمین چگالی زمین (۵/۵g/cm3)داشته باشیم همین دوره بدست می آید .
۵) محاسبات در مورد زمین
حال اگر در مورد زمین این محاسبات را انجام دهیم یعنی به جای شعاع سیاره (Ry)شعاع زمین (۶٫۳۷*۱۰۶m) و به جای چگالی سیاره چگالی زمین(۵/۵)را قرار دهیم دوره تناوب ماهواره ۱:۲۴:۲۴ (حدود یک ساعت و بیست و چهار دقیقه و بیست و چهار ثانیه ) و سرعت آن ۷/۹ کیلومتردرثانیه می باشد.
در مقاله “چاه بی انتها “(چاهی که از یک سر زمین حفر شده ، از مرکز زمین گذشته و از سردیگر زمین بیرون بیاید) می بینیم که دوره تناوب (زمانی که طول میکشد جسم به سر دیگر چاه برسد)به همین اندازه (۱:۲۴:۲۴ ) و سرعت جسم موقع رسیدن به مرکز زمین هم همان ۷/۹ کیلومتر در ثانیه می باشد .

شکل شماره ۲ – چاه بی انتها
۵- مسئله دو یا چند جسم
یکی از مسائل بسیار مهم در مکانیک سماوی مسئله دو جسم می باشد در این بخش در مورد مسئله دو جسم توضیح میدهیم و دربخش بعدحالت های مختلف مسئله دو جسم و تاثیر نیروهای گرانشی را که بر همدیگر وارد می کنند مورد بررسی قرار میدهیم .
۱) گرانش و مسیر دنباله دارها
موقعی که نیوتن در سال ۱۶۸۷میلادی قانون جاذبه عمومی خود را وضع و فرمول بندی کرد توسط این قانون توانست حرکت سیاره ها دور خورشید و قمرها دور سیاره ها را پیش بینی و توجیه کند همچنین توانست مسیر دنباله دارها را هم تا حدوذ زیادی پیش بینی کند ولی نتایج پیش بینی ها دقیقا با واقعیت همخوانی نداشت از این رو نیوتن عنوان کرد وقتی می خواهیم مسیر دنباله دارها را پیش بینی کنیم علاوه بر خورشید باید گرانش سیارات دیگر بخصوص غول های گازی نظیر مشتری و زحل را هم در نظر بگیریم اینجا دیگر دو جسم مطرح نبود و حداقل سه جسم را باید در نظر گرفت(علت این که با وجود صرف نظرکردن ازگرانش غول های گازی بازهم مداردنباله دارها تا حدودی قابل پیش بینی بود این بودکه گرانش خورشید بسیار بیشتر از حتی سیاره غول پیکر مشتری می باشد. در مورد دنباله دارها در مقاله “دنباله دارها “ به طور کامل توضیح می دهیم )همین نکته منجر به طرح مسئله چند جسم درریاضیات و مکانیک سماوی شدکه تا قرن ها ذهن فیزیکدان ها و ریاضیدان ها را مشغول کرد که در ادامه در مورد آن توضیح می دهیم .
۲) مسئله چند جسم
مسئله چند جسم را برای نخستین بار خود نیوتن مطرح کرد طرح مسئله به این صورت است : «چگونه میتوان مسیر حرکت n جسم را که در مکانهای مختلف و با سرعتهای مختلف در فضا در حال حرکت هستند و تحت تأثیر نیروهای گرانشی متقابل یکدیگر قرار دارند، محاسبه کرد؟
از زمان طرح این مسئله هنوز پاسخ قطعی به آن داده نشده است و بزودی هم این مسئله حل نمیشود (حتی برای سه جسم) ولی واقعا چرا مسئله چندجسم تا این حدپیچیده و بغرنج است؟ (امروزه در حالت خاص سه جسم به کمک کامپیوتر و از روش های تقریبی تا حدودی قابل حل است ولی تاکنون روش ریاضی و قطعی برای آن پیدا نشده است )
نکته : نیروهای وارد شده به دو یا چند جسم تنها نیروهای گرانشی نیستند بلکه نیروهای دیگر را هم شامل می شوند مثلا نیروهای الکتریکی بین یون ها و یا لکترون ها با هسته اتم و… را هم شامل می شود .
۳) چرا مسئله سه جسم و بیشتر اینقدر مشکل است ؟
جواب های بیشماری به این مسئله داده شده است ولی ساده ترین جواب این است که : « قانون جاذبه عمومی نیوتن به صورت معادله دیفرانسیلی از مرتبه دوم نوشته شده است از این رو برای حل مسئله n جسم باید پاسخ عمومی برای تعدادی معادله(بیشتر از دو معادله )دیفرانسیل غیر خطی بدست آورد که حل آن کاری بسیار مشکل می باشد.»
همچنین سه جسم برای ما سیستمی را تشکیل می دهند که “سیستم دینامیک” نامیده می شوددر این سیستم یک تغییر کوچک می تواند باعث دگرگونی شدید( آشوب) در مراحل بعدی بشود و همین مسئله باعث شده کسی نتواند آن را حل کند .
۴) اویلر و لاگرانژ و مسئله سه جسم
لئونارد اویلر (۱۵آوریل ۱۷۰۷– ۱۸سپتامبر ۱۷۸۳)ریاضیدانان و فیزیکدانان برجسته سوئیسی در سال ۱۷۶۵برای حل مسئله ۳جسم حالت خاصی از این مسئله را در نظر گرفت و آن این بود که یکی از۳جسم را بسیار خرد در نظر گرفته به گونه ای که بتوان از گرانش آن چشم پوشی کرد و کوشش کرد نقاطی را پیدا کند که در آن نقاط نیروی گرانش وارده شده برجسم خرد توسط دو جسم عظیم برابر باشد .
ژوزف لاگرانژ (۲۵ژانویه ۱۷۳۶–۱۰آوریل۱۸۱۳)ریاضیدان و منجم فرانسوی دنبال کارهای اویلر را گرفت و سرانجام درسال۱۷۷۲توانست این نقاط را کشف کرده و موقعیت آنها را مشخص کند از این رو این نقاط به نام “ژوزف لاگرانژ” ، نقاط لاگرانژی نامیده شدند . در مقاله “نفاط لاگرانژی “ در این باره بیشتر توضیح می دهیم .
۵) مسئله دو جسم
مسئله دو جسم یا مسئله دو جرم (Two-Body Problem) در مکانیک کلاسیک، در مورد تعیین حرکت دو جسم ذره نقطهای (ایدهآل) است که تنها با یکدیگر فعل و انفعال دارند. مثالهای متداول، شامل حرکت یک ماهواره به دور یک سیاره، حرکت یک سیاره به دور یک ستاره، حرکت دو ستاره به دور یکدیگر (ستاره دوتایی) و بررسی کلاسیک حرکت الکترون به دور هسته اتم است. بنابراین تمام حالت هائی که در اینجا در مورد اثرات رابطه بین دو جسم که تحت تاثیر گرانش یکدیگر قرار دارند جزئی از این مسئله می باشد .
۶) مرکز جرم چیست ؟
مرکز جرم((Center of massیک جسم صلب (جسم سخت)یا مجموعه ای از اجسام که یک سیستم را تشکیل می دهند نقطه مشخصی در درون(جسم یا سیستم) می باشد که گوئی همه جرم آن جسم (یا سیستم) در آن نقطه متمرکز شده است . پس در هر جسم صلب نقطه ای به نام مرکز جرم وجود دارد که گرانیگاه (نقطه تعادل)هم نامیده می شود. برای مطالعه کامل مرکز جرم به مقاله “ مرکز جرم “ مراجعه کنید .
۷) مرکز جرم دو جسم
اگر دو جسم با جرم مختلف (جسم بزرگتر M و جسم کوچکتر m) داشته باشیم که به فاصله D از یکدیگر قرار داشته باشند فاصله مرکز جرم آنها از جسم بزرگتر (d) از این رابطه بدست می آید .
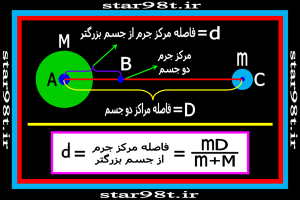
شکل شماره ۳ – تعریف مرکز جرم

در صورتی که نسبت دو جرم را داشته باشیم می توانیم فرمول را به صورت زیر هم بنویسیم .
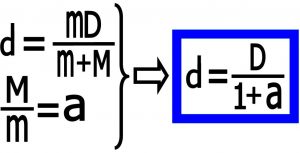
۸) مدار حرکت دو جسم
وقتی می گوئیم ماهواره (چند کیلوئی) دور زمین می چرخد و یا ماه به دور زمین می چرخد وقتی از چرخش سیاره ها در مدار خورشید صحبت می کنیم و یا چرخش ستاره های مزدوج (که جرمشان تقریبا برابر است ) صحبت می کنیم در واقع از مسئله دو جسم را که تحت گرانش یکدیگر قرار دارند صحبت می کنیم . این دو جسم هر نسبتی که با هم داشته باشند برای جلوگیری از برخورد با یکدیگر هر دو ( باز هم تاکید می کنیم هر دو ) دور مرکز جرم مشترکشان می چرخند . حرکت مداری یکطرفه نیست در واقع هر دو جسم مداری را جداگانه حول مرکز جرم مشترکشان تشکیل می دهند که این مدار یکی از مقاطع مخروطی می باشد . در بخش یعدی با توجه به فرمول مرکز جرم حالت های مختلف را به همراه مثال مورد بررسی قرار می دهیم .
۶- انواع حرکت های مداری
در بخش های قبل در مورد حرکت یک جسم کوچک در مدار اجسام بسیار بزرگ توضیح دادیم ،مدارهائی که بر اساس قوانین کپلر توضیح داده می شود.در آنجا فرض کردیم که جسم در مدارقرار داده شده نسبت به جسم مادر بسیار بسیار کوچک است بنابراین جسم کوچکتر در مدارهائی که یکی از مقاطع مخروطی است به دور جسم بزرگتر دوران میکند ولی آیا همیشه همینطور است؟دربسیاری از مواردجسم دوم یا مساوی جسم اول است یا فقط مقداری کوچکتر است و نمی توانیم ازجرم آن صرف نظر کنیم همچنین دربخش قبلی مسئله دو یا چند جسم که تحت نیروی گرانش یکدیگر واقع شدند را توضیح دادیم و گفتیم که اگر سه جسم و بیشتر داشته باشیم حل مسئله بسیار بغرنج بوده به طوری که تا امروز راه حل ریاضی برای آن پیدا نشده است ولی در حالت ساده تر یعنی دو جسم می توانیم می توانیم انواع حالت های مختلف را در نظر بگیریم که در آن یکی از دو جسم بسیار بسیار کوچکتر از جسم عظیم می باشد تا موقعی که اندازه آن دو جسم برابر است.در این بخش در این مورد توضیح می دهیم . و البته برای ساده شدن مطلب ابتدا مدارهای دایره ای را بررسی می کنیم .
۱) مدار حرکت دو جسم
وقتی می گوئیم ماهواره (چند کیلوئی ) دور زمین می چرخد و یا ماه به دور زمین می چرخد، وقتی از چرخش سیاره ها در مدار خورشید صحبت می کنیم و یا چرخش ستاره های مزدوج (که جرمشان تقریبا برابر است ) صحبت می کنیم در واقع از مسئله دو جسم را که تحت گرانش یکدیگر قرار دارند صحبت می کنیم . این دو جسم هر نسبتی که با هم داشته باشند برای جلوگیری از برخورد با یکدیگر هر دو ( باز هم تاکید می کنیم هر دو ) دور مرکز جرم مشترکشان می چرخند . حرکت مداری یکطرفه نیست در واقع هر دو جسم مداری را جداگانه حول مرکز جرم مشترکشان تشکیل می دهند که این مدار یکی از مقاطع مخروطی می باشد . برای ساده تر شدن مسئله ابتدا مدار دایره ای را مورد بررسی قرار می دهیم و با توجه به فرمول مرکز جرم حالت های مختلف را به همراه مثال مورد بررسی قرار می دهیم .
۲) حالتی که مرکز جرم عملا بر مرکز جسم بزرگ منطبق می شود
این همان حالتی است که قبلا بررسی کردیم مثال بارز آن گردش یک ماهواره به دور زمین می باشد در این حالت می توانیم ازجرم جسم دوم در مقابل جسم اول صرف نظر کنیم (همان کاری که قبلا کردیم ) بنابر این داریم :

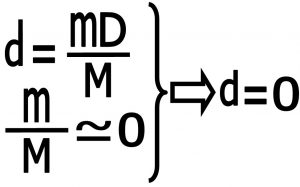
بنابر این فاصله مرکز جرم تا مرکز جسم عظیم مرکزی صفر می شود و مرکز جرم بر مرکز جرم بزرگتر منطبق می شود (شکل های شماره ۴ و ۵)
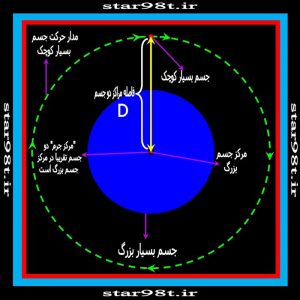
شکل شماره ۴ – مدار یک جسم بسیار کوچک در مقابل جسم بسیار بزرگ
همانطور که توضیح داده شد نمونه آن گردش ماهواره بر گرد زمین می باشد همچنین از مدار زمین به دور خورشید هم می توان نام برد . اگر چه مرکز جرم فاصله قابل ملاحظه ای از مرکز خورشید دارد .
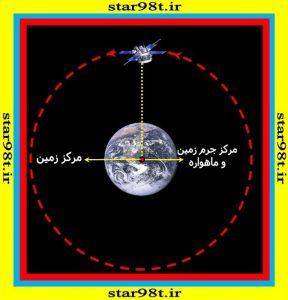
شکل شماره ۵ – ماهواره ای در مدار زمین نمونه ای از عظیم بودن جسم مرکزی
نکته : در مورد مرکز جرم و فرمول آن در بخش قبلی توضیح کافی دادیم
این تصویر متحرک هم این نوع حرکت مداری را نشان می دهد :
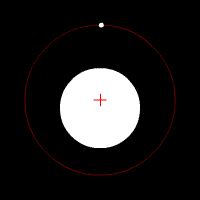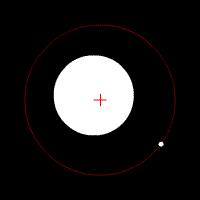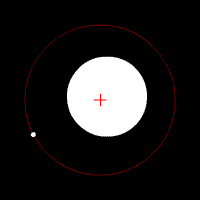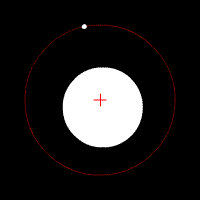
تصویر متحرک شماره ۱ – وقتی مرکز جرم تقریبا در مرکز جسم عظیم مرکزی قرار دارد .
۳) حالتی که مرکز جرم بر مرکز جرم بزرگ منطبق نمی باشد ولی در درون آن قرار می گیرد
اگر جسم دوم بقدری بزرگ باشد که نتوان از جرم آن در مقابل جسم اول صرف نظر کرد مرکز جرم دیگر در مرکز جسم بزرگ قرار نمی گیرد بلکه به مقدار قابل ملاحظه ای از مرکز آن فاصله می گیرد در این صورت اگر
شعاع جسم دوم به اندازه کافی بزرگ باشد در این صورت مرکز جرم در درون جسم بزرگ قرار می گیرد و جسم بزرگتر هم حول مرکز جرم خود که درونش قرار دارد دوران می کند که اگر این مرکز جرم به مرکز جسم دوم نزدیک باشد از دور شبیه نوعی حرکت نوسانی و ارتعاش به نطر می رسد . ( شکل های شماره ۶ و ۷)
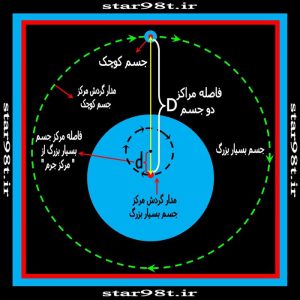
شکل شماره ۶ – حالتی که مرکز جرم بین مرکز جسم بزرگ و سطح آن قرار دارد
مثال بارز آن مجموعه ماه و زمین می باشد که مرکز جرم آن در فاصله ۴۷۰۰ کیلوتری مرکز زمین قرار دارد و اگر از دور به زمین نگاه کنیم حرکت ارتعاشی زمین حول مرکز جرم مشترکش با ماه کاملا مشهود است .
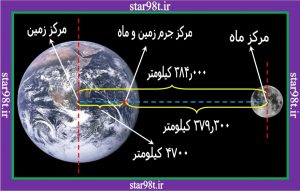
شکل شماره ۷ – مرکز جرم ماه و زمین
نکته : در این حالت ( مدار دایره ای )چرخش دو کره باید به گونه ای انجام می شود که فاصله مرکز جرم از مرکز دو کره تعغیر نکند .
این تصویر متحرک هم این نوع حرکت مداری را نشان می دهد :
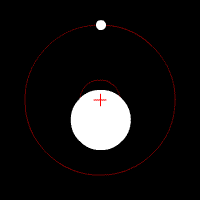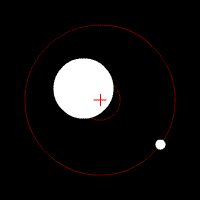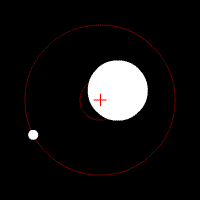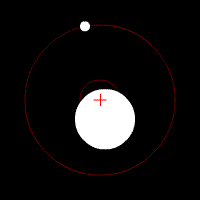
تصویر متحرک شماره ۲ – وقتی مرکز جرم بین مرکز و سطح جسم عظیم قرار دارد .
۴) اندازه دو جسم متفاوت است ولی مرکز جرم در خارج از هر دو جسم قرار دارد
این حالت موقعی پیش می آید که جرم دو جسم با هم تفاوت می کند ولی تفاوت در آن حدی نیست که مرکز جرم در دورن جسم بزرگتر قرار بگیرد (یا شعاع جسم بزرگتر آنقدر بزرگ نیست که مرکز جرم را درون خودش جای دهد)بنابراین دو کره مانند یک مجموعه دوتائی هر کدام به طور جداگانه حول مرکز جرم مشترکشان دوران می کنند . از دور که نگاه کنیم دو جسم را می بینیم که هر دو ضمن این که حالت تقابل خود را حفظ می کنند ( درست مقابل همدیگر قرار دارند)حول نقطه ای نامرئی به گونه ای دوران می کنند(جهت دوران هر دو در یک جهت است) که فاصله خود را حفظ می کنند برای این مجموعه دو مدار تعریف می شود مدار بزرگتر که جسم کوچکتر در آن دوران می کند و مدار کوچکتر که جسم بزرگتر دوران می کند (شکل های شماره ۸ و ۹) در طبیعت از این گونه مدارها زیاددیده می شود آشناترین آنها ستارگان مزدوج (دوتائی) می باشد که یکی بزرگتر ودیگری تا حدی کوچکتر است و هردو به همان ترتیب که گفته شدحول مرکز جرم مشترکشان گردش می کنند(درمورد ستارگان درمقاله ای دیگر شرح می دهیم)
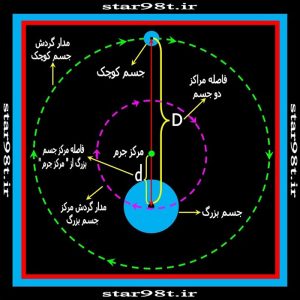
شکل شماره ۸ – حالتی که مرکز جرم در خارج از جسم بزرگترقرار دارد
آشناترین نمونه آن درمنظومه شمسی پلوتون و قمرش شارون می باشد .

شکل شماره ۹ – پلوتو و شارون حالتی که یکی از دو جسم بزرگتر است ولی نه آنفدر بزرگتر که مرکز جرم درون آن قرار بگیرد
این تصویر متحرک هم این نوع حرکت مداری را نشان می دهد :
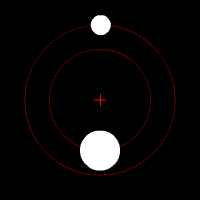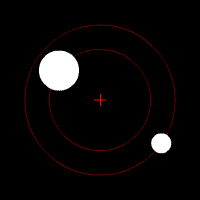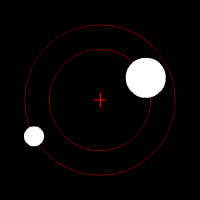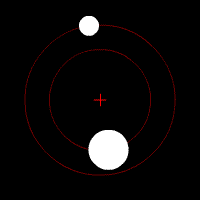
تصویر متحرک شماره ۳ – وقتی جرم دو جسم مساوی نبوده ولی مرکز جرم خارج از جسم بزرگتر قرار می گیرد .
۵) هر دو جسم دقیقا اندازه هم هستند
در این حالت دو جسم تقریبا هم اندازه هستند (زیرا احتمال این که دقیقا جرم برابر داشته باشند خیلی کم است ) در این صورت بجای مدارهای جداگانه دو حسم حول یک مدار مشترک گرد مرکز جرم مشترکشان می چرخند به گونه ای که هر دو در دوسر قطری از دایره ای که مدار را تشکیل داده است قرار می گیرند . (شکل شماره ۱۰ )
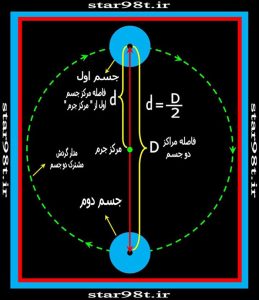
شکل شماره ۱۰ – حالتی که دو جسم جرم یکسان داشته باشند و بنابراین در مدار مشترکی حول مرکز جرم مشترکشان می چرخند
با استفاده از فرمول مرکز جرم می توانیم این مسئله را نشان دهیم : ( یعنی مرکز جرم وسط فاصله دو جسم قرار می گیرد )
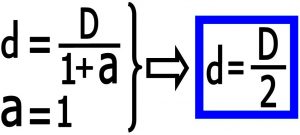
این تصویر متحرک هم این نوع حرکت مداری را نشان می دهد :
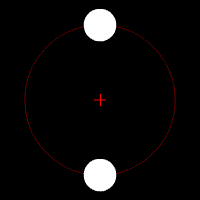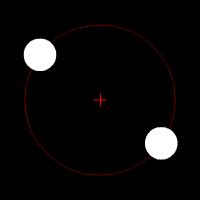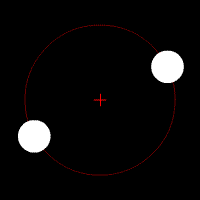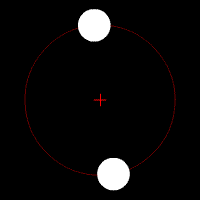
تصویر متحرک شماره ۴ – وقتی جرم دو جسم مساوی می باشد
۶) مدارهای بیضی
در مورد حالت های خاصی که دو جسم تحت تاثیر گرانش متقابل یکدیگر قرار می گیرند تا اینجای کار مدارها را دایره در نظر گرفتیم ولی همانطور که قبلا هم گفته شد مدارهای می توانند یکی از مقاطع مخروطی باشند (البته در مورد مدارهای سهمی و هذولی که به معنی فرار از گرانش یکدیگر می باشد توضیح نمی دهیم) ولی در واقع بیشتر مدارها بیضی (ازبیضی نزدیک به دایره تا بیضی کشیده ) هستند «شکل شماره ۱۱» یکی از این مدارها را نشان می دهد . که در آن دو جرم برابرند .
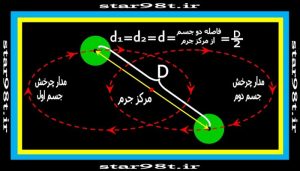
شکل شماره ۱۱ – حالتی که دو جسم جرم یکسان داشته باشند ولی مدار بیضی می باشد.
نکته : درحالتی که مدارها بیضی باشد فاصله دو جسم ثابت نبوده و تعغیر می کند ( همچنین فاصله مرکز جرم از مراکز دو جسم) ولی مکان مرکز جرم همیشه به گونه ای است که وسط دو جسم قرار می گیرد .
۷) محاسبه مرکز جرم ماه و زمین و زمین و خورشید
با استفاده از فرمول مرکز جرم میتوانیم مرکز جرم مجموعه ماه و زمین و زمین و خورشید را حساب کنیم .
۷-۱) مجموعه زمین و ماه : زمین حدود ۸۰برابر ماه می باشد بنابر این مرکز جرم به فاصله ۴۷۴۰ کیلومتری مرکز زمین واقع شده است .نه در مرکززمین ، بنابراین گرانش ماه سبب می شود که زمین علاوه بر گردش به دور خورشید دور مداری که در فاصله ۴۷۴۰ کیلومتری مرکزش قرار دارد دوران کند . ( شکل شماره ۷)

۷-۲) مجموعه زمین و خورشید : خورشید حدود ۰۰۰ر۳۳۰برابر زمین جرم دارد . بنابر این مرکز جرم به فاصله ۴۵۰ کیلومتری مرکز خورشید واقع شده است . با توجه به شعاع تقریبا ۷۰۰ هزار کیلومتری خورشید فاصله ۴۵۵ کیلومتر را می توانیم تقریبا در مرکز خورشید بگیریم .

۷- ماهواره
در این بخش در مورد ماهواره و اهمیت ماهواره در تکنولوژی امروز توضیح می دهیم تکنولوژی که در بسیاری از وسائل ساخت بشرکه به فضا فرستاده شده ودرمدار زمین ویا سیارات دیگر منظومه شمسی قرارداده شده اند به کار می آید. و با استفاده از قوانین گرانش و قوانین کپلر کار می کنند.
در مورد ماهواره و اهمیت آن در مقاله ای جداگانه به نام “ ماهواره “ به طور مفصل توضیح می دهیم در این بخش توضیحی مختصر راجع به ماهواره و مدارهای ماهواره ای و… می دهیم .
۱) ماهواره( Satellite )چیست ؟
هر دستگاهی که توسط بشر ساخته شده و به فضا فرستاده شود و در مداری (دایره ای یا بیضی) به دور زمین و یا سیارات دیگر می چرخند ماهواره (شبیه ماه) و یا قمر مصنوعی نامیده می شود. ماهواره کاربردهای بسیار متنوعی دارند به گونه ای که تکنولوژی ما بدون ماهواره و تجهیزات مرتبط با آن بکلی فلج می شود .
۲) تاریخچه ماهواره
بعد از کشف قانون گرانش جهانی و پی بردن به چگونگی حرکت سیاره ها بر گردخورشید کم کم این ایده در ذهن ها شکل گرفت که اگر بتوان یک جسم را به فضای خارج از زمین برده و سرعت مناسبی به آن بدهند برای همیشه در مداری (دایره ای و یا بیضوی) به دور کره زمین می چرخد. از آن زمان تا نخستین پرتاب ماهواره درسال۱۹۵۷(اسپوتینگ یک) دانشمندان و نویسندگان زیادی در مورد اهمیت ساخت و فرستادن فمر مصنوعی ( که بعدها ماهواره نام گرفت) به مدار زمین گفتند و نوشتند و امروزه دیگر برای همگان مشخص شده که ماهواره چه کاربردهائی می تواندداشته باشد و چگونه ماهواره ها زندگی بشر را دگرگون کرده اند .
۳) کاربردهای ماهواره
مهمترین چیزی که ماهواره را به وسیله ای بسیار مهم و پرکاربرد تبدیل کرده است این است که ارتفاع ماهواره از سطح زمین (نسبت به اشیاء زمینی مانند کوه ها و…)خیلی زیاد است و در آن ارتفاع زیاد قسمت های بسیار زیادی از سطح زمین دیده می شود . همچنین ماهواره با حرکت سریع به دور زمین می تواند در آن ارتفاع بالا قسمت بسیار زیادتری را هم تحت پوشش خود در آورد بنابراین از یک ماهواره می توان برای عکس برداری و فیلم برداری (ازنقاط مختلف زمین)و…تا مخابره امواج رادیوئی ،برای کاربردهای (علمی و تحقیقاتی،جاسوسی و نظامی،خدمات رسانی در بخش مخابرات و…)استفاده کرد.
۴) ماهواره چگونه پرتاب می شود ؟
ماهواره ها را از روی زمین با موشک های بزرگ به فضا می فرستند و در ارتفاعی که از قبل مشخص شده (نوع موشک و سوخت موشک هم به همین منظور طراحی شده) قرار می دهند و بعد سرعت لازم را با توجه به ارتفاع و نوع مدار(دایره ای و بیضی بودن)به ماهواره داده و ازآن پس ماهواره تا مدت زمانی که عمر ماهواره نامیده می شود در مدار خود باقی مانده و خدمات لازم را ارائه می کند .
۵) تکنولوژی پرتاب ماهواره
موشک هائی که ماهواره را به ارتفاع مورد نظر می فرستند موشک های ماهواره بر نامیده می شوند این موشک ها جزء بزرگترین موشک ها می باشند و هر چه ارتفاعی که ماهواره باید فرستاده شود بیشتر باشد موشک بزرگتری مورد نیاز می باشد . از این رو تکنولوژی ساخت و فرستادن و در مدار قرار دادن ماهواره در اختیار معدودی از کشورهای جهان که تکنولوژی و امکانات وسیعتری دارند قرار دارد . بنابراین کشورهائی که تازه در این گروه قرار می گیرند ابتدا با فرستادن ماهواره در ارتفاع کمتر شروع می کنند .
۶) ماهواره تا چه ارتفاعی بالا می رود ؟
با توجه به وظیفه و کارکرد ماهواره ارتفاع ها و مدارهای مختلفی برای ماهواره ها وجود دارد ولی نکته ای که بسیار مهم می باشد این است که ماهواره باید تا ارتفاعی بالا برود که جو زمین یا تمام شود و یا به حداقل مقدار خود برسد در غیر این صورت سرعت ماهواره بر اثر برخورد با مولکول های هوا کم و کمتر شده و در یک مدار مارپیچی به درون جو زمین سقوط می کند از همین رو هرچه ارتفاع ماهواره بیشتر باشد مدت زمانی هم که ماهواره در مدار باقی می ماند بیشتر می شود . امروزه مشخص شده کمترین ارتفاع برای باقی ماندن ماهواره ارتفاع ۳۰۰ کیلومتری می باشد که ارتفاع پائین نامیده می شود .
۷) محاسبه دوره تناوب و سرعت ماهواره ها
سرعت و دوره تناوب ماهواره ها با توجه به قوانین کپلر و قانون جاذبه عمومی نیوتن مشخص می شود . در بخش سوم همین مقاله (۳- کاربرد قانون سوم کپلر ) دوره تناوب و سرعت متوسط یک قمر را که دور سیاره مادر می چرخد بدست آوردیم کافی است در فرمول به جای M جرم زمین((M=Meو به جای r فاصله ماهواره از مرکز زمین (r=Re+H) قرار دهیم )H ارتفاع ماهواره از سطح دریا می باشد- شکل شماره ۱۲) بنابر این داریم :
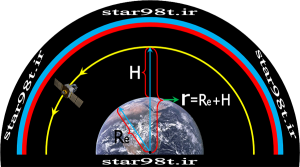
شکل شماره ۱۲ – محاسبه دوره تناوب و سرعت ماهواره
در شکل متحرک زیر نیروهای وارد شده به ماهواره نشان داده شده است :
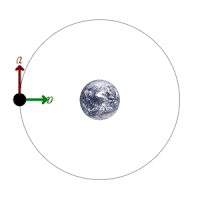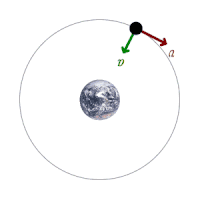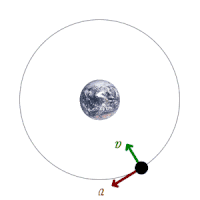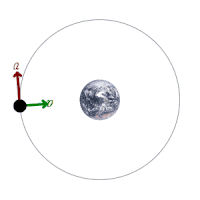
تصویر متحرک شماره ۵ – یک ماهواره در حال گردش به دور زمین و نیروهای وارد شده به آن
۷-۱) دوره تناوب ماهواره :
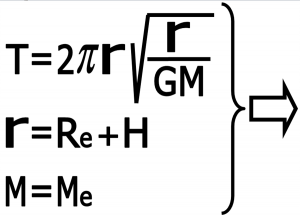
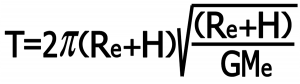
بنابر این دوره تناوب ماهواره عبارت است از :
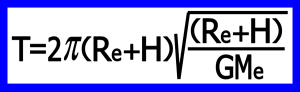
۷-۲) سرعت متوسط ماهواره :
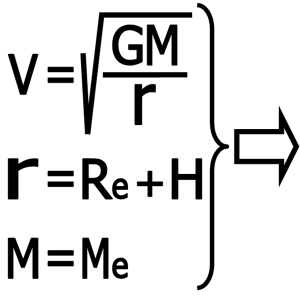
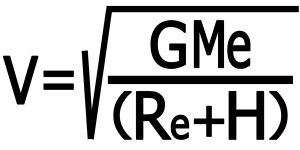
بنابراین سرعت ماهواره برابر است با :

مقادیر ثابت در این فرمول ها عبارت است از :

۸) انواع مدارهای ماهواره ؟
ماهواره ها بنابر وظیفه و کاری که برای آن طراحی شده اند همچنین امکانات و تجهیزاتی که دادند در مدارهای مختلفی قرار داده می شوند و خدمات مختلفی انجام می دهند . تعریف های زیادی برای مدارهای ماهواره وجود دارد که یکی از آنها مدارهای ماهواره را بر اساس ارتفاع طبقه بندی می کند .
۸-۱)ماهواره های مدار پائین(لئو):ارتفاع این ماهواره ها بین۳۲۰تا۸۰۰کیلومتر می باشد دوره تناوب آنها بین ۹۰ تا۱۰۰دقیقه می باشد.معروفترین ماهواره ای که دراین رده جای دارد ایستگاه فضائی بین المللی می باشد.
۸-۲) مدارهای قطبی:مدارچرخش این گروه از ماهواره ها در امتداد نصف النهارها و از روی قطب های شمال و جنوب می گذرد مزیت این مدار این است که در مدتی که ماهواره یک دور به دور زمین می چرخد زمین هم مقداری به دور خودش می چرخد و بنابراین ماهواره سطح بیشتری را می تواند پوشش دهد .
۸-۳)ماهواره های زمین ثابت:این مدار یکی از مهمترین مدارها می باشد تقریبا تمام ماهواره های مخابراتی و رادیوئی و تلویزیونی و… همه در این مدار قرار دارند . در قسمت بعد راجع به این مدار توضیح می دهیم .
۹) مدار زمین ثابت
مدار زمینثابت (Geostationary orbit) یا مدار زمینایستا که بدان کمربند کلارک نیز گفته میشود . یکی از مهمترین مدارهای ماهواره می باشد . برای این که دستگاه های گیرنده برنامه های ماهواره موقع پخش برنامه های تلویزیونی و… مرتب تعغیر جهت ندهند مکان ماهواره باید در آسمان ثابت باشد برای این کار دوره تناوب ماهواره با دوره تناوب گردش زمین به دور خودش (یک شبانه روز نجومی که ۲۳:۵۶:۰۴ می باشد) برابر باشد . بنابراین با توجه به فرمول دوره تناوب ماهواره ارتفاع ماهواره ها از سطح زمین باید ۳۵۷۸۶ کیلومتر باشد ( با توجه به فرمول رابطه دوره تناوب و ارتفاع که ذکر شد بسادگی می توانید این مقدار را بدست بیاورید )
تصاویر متحرک زیر نشان می دهد یک ماهواره زمین ثابت چگونه بالای یک نقطه ثابت می ماند .

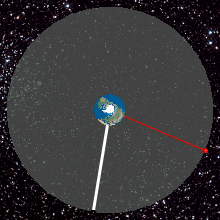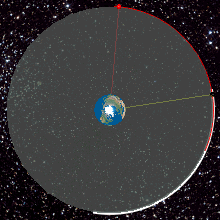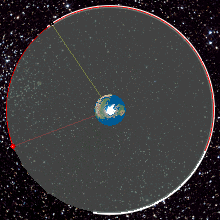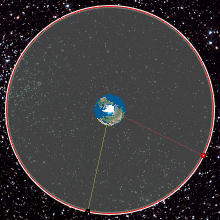
تصویرهای متحرک شماره ۶ و ۷ – ماهواره های زمین مرکز از نمای بالا و روبرو
۸- خلاصه مطلب
مکانیک مداری یا اخترپویاشناسی( astrodynamics) شاخهای ازعلم مکانیک است که به حرکت اجرام آسمانی (کهکشان ها تا ستارگان و سیارات و قمرها و…ماهواره ها) و مدارهائی که بر اثر گرانش متقابل یکدیگر تشکیل می دهند می پردازد.حرکت اجرام سماوی بر اساس قانون جاذبه عمومی نیوتن و همچنین قوانین کپلر(که بر گرفته از همان قانون گرانش جهانی است)می باشد.
۱) مختصری از مکانیک مداری یک
مکانیک مداری شاخهای از علم مکانیک است که به حرکت اجرام آسمانی و مدارهائی که بر اثر گرانش متقابل یکدیگر تشکیل می دهند می پردازد . درمقاله “مکانیک مداری و قوانین کپلر(۱)“ در مورد مکانیک مداری ، قوانین کپلر و اثبات این قوانین توضیح دادیم آنچه در این بخش توضیح می دهیم در واقع خلاصه مطالبی است که در این مقاله گفته شده است بنابر این قبل از مطالعه مقاله حاضر مقاله “مکانیک مداری و قوانین کپلر(۱)“ را حتما مطالعه کنید .
۲) کاربرد قانون سوم کپلر
قانون سوم کپلر استفاده های گسترده ای در نجوم و فضانوردی و…دارد . ازجمله :
استفاده ازقانون سوم کپلر در اندازه گیری فاصله زمین تا خورشید (که سنگ بنای تمام اندازه گیری ها در کیهان است)، اندازه گیری جرم خورشید از روی فاصله زمین تا خورشید و دوره تناوب زمین، اندازه گیری فاصله سیاره ها از خورشید، اندازه گیری جرم سیاره ها به کمک دوره تناوب قمرهایشان و…بسیاری از موارددیگر همچون اندازه گیری جرم ستاره های دوتائی به کمک دوره تناوب آنها و…تا محاسبه جرم کلی کهکشان و…تا استفاده در فضانوردی و…در بخش(کاربرد قانون سوم کپلر) درمورد کاربردهای مختلف قانون سوم کپلر توضیح می دهیم .
۳)حرکت در سطح سیاره
در این بخش مسئله ای خاص را در نظر می گیریم فرض کنیم سطح زمین(یا هر سیاره مادر دیگر)عاری از جو و هرگونه پستی و بلندی بود و ما یک ماهواره (یا قمر) را تقریبا در سطح زمین(ارتفاع صفر کیلومتر)قرار می دادیم. می خواهیم دوره تناوب و سرعت این ماهواره را بدست بیاوریم . با توجه به فرمول هائی که از قانون سوم کپلر بدست آوردیم براحتی می توانیم به جای r مقدار Ry (شعاع سیاره y) را قرار دهیم . همچنین در این بخش دوره تناوب و سرعت این قمر ( قمری که دقیقا همسطح سیاره گردش کند ) را بر اساس جرم حجمی (چگالی) سیاره حساب کرده و نشان می دهیم که این دوره تناوب به جرم و شعاع سیاره مادر بستگی ندارد و فقط به چگالی سیاره بستگی دارد . همچنین این دوه تناوب با دوره تناوب جسمی که در چاه بی انتها ( چاهی که از یک سر زمین حفر شده و بعد از گذشتن از مرکز زمین از طرف دیگر خارج شود ) سقوط می کند برابر است .
۴) مسئله دو یا چند جسم
یکی از مسائل بسیار مهم در مکانیک سماوی این است که اگر موقعیت ، جرم و سرعت دو یا چند جسم را بدانیم با توجه به نیروهای گرانشی که به هم وارد می کنند آیا می توانیم موقعیت آنها را در هر زمان پیشگوئی کنیم؟ این مسئله از زمان نیوتن مطرح شد و با وجودی که به نظر می رسد حل این مسئله (با توجه به فرمول های قانون گرانش جهانی) ساده باشدولی واقعیت این است که حل این مسئله فقط در مورد دو جسم امکان پذیر می باشد و در مورد سه جسم و بیشتر از زمان نیوتن تا امروزحل نشده مانده است. در این بخش توضیح می دهم که چرا مسئله سه جسم و بیشتر اینقدر مشکل است و چرا تا امروز (با وجود همه پیشرفت های بشر در نجوم و ریاضیات )هنوز هیچ راه حل ریاضی برای آن پیدا نشده است . همچنین در این بخش در مورد مرکز جرم هم توضیح می دهیم و در بخش بعدی انواع حرکت های مداری را مورد بررسی قرار می دهیم .
۵) انواع حرکت های مداری
در بخش های قبل در مورد حرکت یک جسم کوچک در مدار اجسام بسیار بزرگ توضیح دادیم ،مدارهائی که بر اساس قوانین کپلر توضیح داده می شود.در آنجا فرض کردیم که جسم در مدارقرار داده شده نسبت به جسم مادر بسیار بسیار کوچک است بنابراین جسم کوچکتر در مدارهائی که یکی از مقاطع مخروطی است به دور جسم بزرگتر دوران میکند ولی آیا همیشه همینطور است؟دربسیاری از مواردجسم دوم یا مساوی جسم اول است یا فقط مقداری کوچکتر است و نمی توانیم ازجرم آن صرف نظر کنیم همچنین دربخش قبلی مسئله دو یا چند جسم که تحت نیروی گرانش یکدیگر واقع شدند را توضیح دادیم و گفتیم که اگر سه جسم و بیشتر داشته باشیم حل مسئله بسیار بغرنج بوده به طوری که تا امروز راه حل ریاضی برای آن پیدا نشده است ولی در حالت ساده تر یعنی دو جسم می توانیم می توانیم انواع حالت های مختلف را در نظر بگیریم که در آن یکی از دو جسم بسیار بسیار کوچکتر از جسم عظیم می باشد تا موقعی که اندازه آن دو جسم برابر است.در این بخش در این مورد توضیح می دهیم . و البته برای ساده شدن مطلب ابتدا مدارهای دایره ای را بررسی می کنیم .
۶) ماهواره
امروز اهمیت ماهواره بر کسی پوشیده نیست. (از ماهواره های مخابراتی و… تا ماهواره های علمی و تحقیقاتی و همچنین ماهواره های نظامی)هزاران ماهواره در مدار زمین درحال گردش هستند(البته بجز صدها میلون زباله فضائی) به گونه ای که امروزه بدون ماهواره بخش بزرگی از تکنولوژی ما مختل می شود .
در این بخش در مورد ماهواره و اهمیت ماهواره در تکنولوژی امروز به طور مختصر توضیح می دهیم تکنولوژی که در بسیاری از وسائل ساخت بشرکه به فضا فرستاده شده ودرمدار زمین ویا سیارات دیگر منظومه شمسی قرارداده شده اند به کار می آید ، ماهواره هائی که با استفاده از قوانین گرانش و قوانین کپلر کار می کنند.
در مورد ماهواره و اهمیت آن در مقاله های جداگانه به نام “ ماهواره(۱) – مدارهای ماهواره “ و “ ماهواره(۲) – کاربرد ماهواره “ و به طور مفصل توضیح می دهیم در این بخش توضیحی مختصر راجع به ماهواره و مدارهای ماهواره ای و… می دهیم .
![]()
برای مطالعه سایر مقاله های نجومی روی شکل زیر کلیک کنید.
![]()
برای مطالعه مقاله های روانشناسی اینجا را کلیک کنید .
![]()
عکس های طبیعت, طبیعت خوانسار , شکوفه های بهاری , گلستان کوه ,دانلود آلبوم های کامل بهترین و زیباترین عکس ها ,آلبوم هائی با صدها عکس کیفیت بالا , در هیچ کجای اینترنت این عکسها را پیدا نمیکنید , عکس هابدون استفاده از تکنیک های فتوشاپ تهیه شده , کاملا طبیعی
![]()
برای آموزش کامل و حرفه ای گوگل مپ روی شکل زیر کلیک کنید
![]()
۱) هر گونه اظهار نظر را در فرم اظهار نظر کاربران وارد کنید .
۲) نظرات بعد از تایید مدیریت نشان داده می شود .
۳) با انتقادات و پیشنهادات سازنده خود ما را هرچه بیشتر همراهی کنید . مدیریت از انتقادات و پیشنهادات سازنده شما استقبال میکند .
۴) نوشته های قرمز پر رنگ ارجاع به لینک هستند که هنوز لینک آنها قرار داده نشده است ( هنوز صفحه آنها منتشر نشده است )
۵) نوشته های آبی پر رنگ ارجاع به لینک هستند که لینک آنها قرار داده شده است ( صفحه آنها منتشر شده است )
۶) هرگونه بهره برداری : کپی تمام و یا قسمتی از مطالب این سایت بدون ارجاع منبع آن ممنوع می باشد .
۷) تکثیر فایل های Pdf با ذکر منبع آزاد ولی فروش آن تحت هر عنوان و با ذکر منبع هم ممنوع می باشد.
![]()