خسوف ( ماه گرفتگی )

خسوف یا ماه گرفتگی یکی از زیباترین پدیده های طبیعت است . زمانی بشر از ماه گرفتگی وحشت داشت و افسانه های و توجیهات غیر علمی و یا بعضا شبه علمی در مورد این پدیده زیبا می ساخت .
در این بخش در مورد :
تاریخچه ماه گرفتگی , افسانه های مربوط به آن , انواع ماه گرفتگی ها , علت آن و… پدیده هائی در این ارتباط توضیح داده و در نهایت با استفاده از ماه گرفتگی به محاسبه فاصله ماه تا زمین می پردازیم .

۱-  افسانه‏‌های عجیب و غریب در مورد ماه‌گرفتگی

در زمان های گذشته که علت پدیده های طبیعت ناشناخته بود و علم هنوز در مراحل اولیه بود . مردم عامی برای هر پدیده ای به افسانه ها و خرافات متوسل می شدند . از جمله در مورد کسوف و خسوف نیز افسانه های بیشماری ساخته و پرداخته بودند. ناپدید شدن ماه برای آن مردمان نشانه مصیبت و بدبختی بود (حیوانات قاتل و خونخوار , دیوهای وحشتناک , اژدها و…. از جمله موجوداتی بودند که عامل ناپدید شدن ماه بودند و در زمان خسوف به زمین می آمدند) و این اقوام برای دفع بدبختی و رفع خطر هر کاری می کردند . در بسیاری از اقوام ابتدائی حتی برای این منظور قربانی ها می کردند . در اینجا به پاره ای از این افسانه ها می پردازیم .

۱) زوزه کشیدن بر سر ماه

در افسانه های اینکاها( اقوام باستانی امریکای جنوبی ) , جاگواری ( پلنگ آمریکای جنوبی ) وجود دارد که به ماه حمله کرده و می خواهد ماه را بخورد ( از این رو رنگ ماه به رنگ خون در می آید ) و اگر ماه را بخورد به انسان ها حمله می کند . از این رو تمام کوشش خود را می کردند تا این موجود خطرناک را دفع کنند .
نیزه ها را به سوی ماه پرتاب می کردند و سرو صدا ایجاد می کردند . سگ ها را کتک می زدند تا بلند زوزه بکشند و … گزارشات این رفتار اینکاها در زمانی که اسپانیائی ها به خاک آمریکا پا گذاشتند ثبت شده است

 

 شکل شماره ۱ – زوزه کشیدن بر سر ماه

 ۲) پادشاه بدلی

اهالی بین النهرین ماه گرفتگی رانتیجه حمله به ماه می دانستندو متهمان اصلی دراین میان هفت دیو بودند .
مردم آن دوران هرچه را در آسمان اتفاق می افتاد به زمین نسبت می دادند و چون شاه را نماینده خدا در روی زمین می دانستند . ماه گرفتگی را حمله به شخص شاه قلمداد می کردند و بخاطر در امان ماندن شاه از حمله دیوان در مدت ماه گرفتگی پادشاه را به جای امن برده و یک پادشاه خیالی را به جای پادشاه اصلی بر سر تخت می گذاشتند ( آنها چون تخصص در پیش بینی گرفتگی ها داشتند حتی قبل از گرفتگی  زمینه را برای پادشاه بدلی فراهم می کردند )
جالب اینجا بود که در مدت ماه گرفتگی با پادشاه بدلی مانند یک شاه واقعی رفتار می کردند ولی بعد از خسوف اغلب او را می کشتند تا از شرش در امان بمانند .

۳) درمان ماه

یک قبیله بومی در شمال کالیفرنیا به نام “ هوپا “ اعتقاد داشتند که ماه ۲۰ همسر و تعداد زیادی حیوان خانگی دارد . حیوانات خانگی او شامل شیرهای کوهی و مارها و … حیوانات خطرناک بوند . وقتی غذای کافی به حیوانات نمی رسید آنها به ماه حمله می کردند و او را خونین و مالی می کردند و در این موقع همسران ماه می آمدند و حیوانات را پراکنده می کردند و ماه را درمان می کردند که خسوف پایان می پذیرفت .
برای قبیله لویزنو در جنوب کالیفرنیا، ماه گرفتگی نشان این بود که ماه مریض شده است. وظیفه اعضای قبیله خواندن مناجات یا دعا برای بازگرداندن سلامتی او بود.

۴) افسانه‌های مردم  باتامالیبا

سرزمین باتامالیبا بین دو کشور توگو و بنین در آفریقا می باشد . بین این مردم افسانه ای شایع است که در موقع ماه گرفتگی , خورشید و ماه در حال جنگ هستند و مردم از آنها می خواهند که جنگ را تمام کنند ولی شرطش این است که بین خودشان جنگ را تمام کنند از این رو در موقع ماه گرفتگی فرصتی است برای دور هم جمع شدن و رفع کدورت ها و خشم های قدیمی, این داستان ها و اعتقادات تا همین امروز دوام داشته است .

۵) افسانه های کالینا ( Kalina)

مردم کالینا ( Kalina) ساکن شمال نواحی ساحل آمریکای جنوبی هستند . در افسانه های کالینا ماه و خورشید برادرند و بیشتر اوقات با هم خوبند ولی بعضی اوقات بین آنها دعوا می شود و این دعوا بقدی پر حشونت است که می تواند دنیا را با خطر بزرگی مواجه کند از این رو آنها با ایجاد صداهای بسیار بلند ( همانند کوبیدن روی طبل و زدن فلزات به هم و… ) همچنین پایکوبی و… سعی می کنند به این دعوا خاتمه دهند .
محو شدن خورشید(کسوف) و یا محو شدن ماه (خسوف)به این معنی است که یکی از برادران دیگری را شکست داده است. در این زمان است که مردم فریاد می زنند “پدر بیدار شو!” آن ها به دلیل احترامی که برای برادران قائل هستند از این نام استفاده می کنند نه به این دلیل که بر این باورند که خورشید یا ماه جزو اجداد آن ها هستند.
آن ها تن و بدنشان را در موقع کسوف (خورشید گرفتگی ) می پوشاندند و اعتقاد داشتند که این خون خورشید است که در جنگ با ماه به زمین ریخته و آن را مقدس می دانستند و بعد از کسوف تن و بدن خود را در رودخانه می شستند .

۲- تاریخ مطالعات ماه گرفتگی و خورشید گرفتگی

خورشید گرفتگی و ماه گرفتگی از زمان های قدیم بشدت مورد توجه بشر بوده و همچنان که ذکر شد برای آن دلائل خرافی و افسانه می ساختند در این قسمت با اندیشه های علمی و گاها شبه علمی در مورد خسوف و همچنین کسوف آشنا می شویم .

۱) خسوف و کسوف نزد ملت های قدیمی

صرف نظر از افسانه ها و خرافات ساخته شده در مورد خسوف و کسوف ملت های باستانی هم در مورد خسوف و کسوف اعتقاداتی داشته و کارهائی هم انجام دادند از جمله پیش بینی خسوف و کسوف که در این میان بابلی ها و بعد یونانی ها و بعدها ملت های دیگر قدم های مهمی در این راه برداشتند . قدیمی ترین نوشته به سه تا چهار هزار سال پیش می رسد .

۲) خسوف و کسوف نزد بابلی ها

یکی از مهمترین مراکز تمدن در جهان بابل بود . بابلی ها در ۷ قرن پیش از میلاد برای نخستین بار پرسش های اساسی در مورد خسوف و کسوف مطرح کردند و پی به این حقیقت بردند که کسوف تنها در آغاز ماه قمری و خسوف تنها  موقعی روی می دهد که ماه در حالت بدر کامل باشد . و قاعده معروفی که دو خسوف ماه بعد از ۶ و یا ۵ ماه قمری رخ می دهد . از این رو بابلی ها شروع به پیدا کردن راه هائی برای پیش بینی کسوف و خسوف کردند (در بخش کسوف در مورد پیش بینی بابلی ها توضیح می دهیم )
اما همین منجمان زبر دست بابلی یک نظریه علمی که بتوان بر اساس آن زمان و مکان یک کسوف و یا خسوف را بدقت پیش بینی کرد نداشتند . زیرا لازمه این امر آن است که با حرکات ماه و خورشید آشنائی کامل داشته باشیم . منجمان بابلی با حرکات خورشید مشکل نداشتند ولی حرکات ماه پیچیده بود و از همان زمان جزء معظلات به حساب می آمد و بی نظمی های متعددی را پدید آورده بود .

۳) خسوف و کسوف نزد یونانی ها

بعد ازسقوط امپراتوری بابل ادامه کار به منجمان ایرانی و بعد یونانی سپرده شد . بی نظمی های حرکات ماه را که بابلی ها نتوانسته بودند کشف کنند یونانی ها دنبال کردند و دو عدد از این بی نظمی ها را کشف کردند یکی از این ها توسط ابرخس کشف شد و معادله آن هم نوشته شد و بی نظمی دوم هم توسط بطلمیوس کشف شد . بطلمیوس همچنین قطر ظاهری خورشید و ماه را نسبت به زمین محاسبه کرد و این هم از جمله چیزهائی بود که منجمین بابلی دنبال آن بودند و یکی از نقاط برتری نجوم یونانی نسبت به نجوم بابلی می باشد . نجوم یونانی بر خلاف نجوم بابلی یک علم دقیق بود .

۴) خسوف و کسوف از دیدگاه ابوریحان بیرونی

ابوریحان بیرونی اولین کسی بود که در هزار سال پیش پدیده خسوف و کسوف را بدرستی و منطبق با نظر منجمین عصر حاضر شرح داد . همچنین  او برای خسوف و کسوف جزئی هم که تا آن زمان هیچکس برای آن پاسخی نداشت بدقت پاسخ داد . ابوریحان بیرونی تحقیقات خود را در خصوص کسوف و خسوف در کوه های لغمان در اطراف کابل قدیم انجام داده است .

۵) خسوف و کسوف از نگاه خواجه نصیرالدین طوسی

ابو جعفر محمد بن محمد بن حسن توسی مشهور به خواجه نصیرالدین (زادهٔ ۵ اسفند ۵۷۹ در توس – درگذشتهٔ ۱۱تیر۶۵۳دربغداد) شاعر،همه‌چیزدان، فیلسوف، متکلم، فقیه، ستاره‌شناس، اندیشمند، ریاضیدان، منجم، پزشک و معمار ایرانی سده هفتم است. کنیه‌اش «ابوجعفر» و به القابی چون «نصیرالدین»، «محقق طوسی»، «استاد البشر» و «خواجه» شهرت دارد. ( شکل شماره ۲ )
خواجه نصیرالدین طوسی بیشتر از هر دانشمندی در زمان خود به مطالعه خسوف و کسوف و دلائل علمی آن پرداخت .او نه تنها دلیل اتفاق افتادن خسوف و کسوف کلی راتشریح کرده بلکه در موردخسوف و کسوف جزئی نیز تحقیقات ارزشمندی کرد و دلائل آن را بدقت شرح داده است.در رساله معینه فصل۱۳ابتدا تعریفی ازخسوف و کسوف ارائه می دهد و بعد به تشریح دقیق خسوف و کسوف جزئی و کلی می پردازد و می نویسد :
 “چون نور ماه از آفتاب است ، پس هر گاه به زمین مایل حایل شود میان ماه و آفتاب نور ازو باز دارد .”
طبق نظر خواجه نصیرالدین خسوف و کسوف وقتی رخ می دهد که ماه و زمین و خورشید در یک خط راست قرار گیرند . بعد در تعریف کسوف می نویسد : 
“کسوف خورشید به هنگام مقارنه روی می دهد و در این هنگام ماه ، مابین چشم ناظر و خورشید است .در این حالت نور خورشید به ساکنان زمین و نیز سطح قابل رویت ماه نمی رسد و این سطح که رنگ خاص خود را به خود می گیرد تیره و تار به نظر می آید و هم از این روست که قرص خورشید سیاه دیده می شود.”
 او همچنین به نقش گره ها (در مورد گره ها و نقش آنها در کسوف و خسوف در قسمت های بعد توضیح می دهیم ) اشاره کرده و می نویسد :
کسوف هنگامی روی می دهد که ماه در حالت ماه نو نزدیک یکی از گره ها (گره صعودی و یا نزولی) واقع باشد و خسوف موقعی رخ می دهد که ماه در حالت ماه بدر در نزدیکی یکی از این گره ها باشد . طوسی همچنین اهمیت اختلاف منظر را در محاسبه خورشید گرفتگی گوشزد می کند .
در رساله معینه طوسی فاصله میان دو کسوف و دو خسوف را شش ماه قمری می داند :
“و باید دانست که اغلب میان دو کسوف یا دو خسوف شش ماه قمری افتد .”
همچنین در فصل اول از بخش سوم رساله معینه به گرفتگی ستاره ها و سیارات توسط ماه اشاره می کند :
” ماه جملگی کواکب را در وقت قِران می پوشاند و هیچ کوکب او را نمی پوشاند و عطارد زهره را و زهره مریخ را و مریخ مشتری را و مشتری زحل را و زحل برخی از ثوابت را می پوشاند .”
همچنین در فصل ۱۴ از همین بخش در مورد گذر زهره نیز از کتاب شفای ابن سینا  نقل می کند که ابن سینا زهره را چون خال سیاهی بر روی خورشید دیده و عنوان کرده بنابر این زهره از خورشید به زمین نزدیکتر است .  که همه این ها نشان می دهد او کاملا آگاه بوده ماه از همه اجرام دیگر به زمین نزدیکتر است .

شکل شماره ۲ – خواجه نصیرالدین طوسی

۳- سایه و منبع نور

جسم منیر ( چشمه نور ) جسمی است که از خودش نور تولید می کند . اجسامی که در مقابل این جسم قرار می گیرند( جسم حائل کدر) جلو نور را سد کرده و در پشت خود ( جهت مخالف جسم ) یک سایه ایجاد می کند شکل سایه و اندازه آن به نوع چشمه نور و فاصله آن تا منبع نور بستگی دارد که در این قسمت در مورد آن توضیح می دهیم .

۱) سایه حاصل از جسم منیر نقطه ای

چشمه نور نقطه ای چشمه ای است که اندازه نداشته باشد و همه نور از یک نقطه تراوش کند در این حالت برای چشمه نور اندازه در نظر نمی گیریم . وقتی جسم حائل مانع رسیدن نور می شود . مخروط سایه ای ایجاد می کنند که راس آن جسم حائل و به صورت یک مخروط بزرگ شونده تا بینهایت پیش می رود . مرز تاریکی و روشنائی کاملا مشخص و نیم سایه هم تشکیل نمی شود .

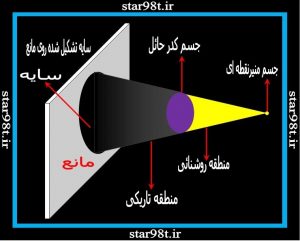
شکل شماره ۳ – چشمه نور نقطه ای و سایه مخروطی آن

۲) سایه حاصل از جسم منیر گسترده

اگر یک جسم منیر , نقطه ای نباشد گسترده است . سایه حاصل از جسم منیر گسترده با جسم نقطه ای تفاوت زیادی دارد . اگر یک حائل باعث ایجاد سایه در جسم گسترده شود مخروط حاصل به اندازه  جسم حائل در مقایسه با چشمه نور گسترده و فاصله جسم حائل با چشمه نور بستگی دارد که مخروط حاصل سه حالت دارد . نکته دیگر این که بر خلاف چشمه نور نقطه ای در اینجا علاوه بر سایه نیم سایه هم داریم .
نیم سایه وقتی ابجاد می شود که جسم حائل نتواند تمام چشمه نور را بپوشاند و قسمتی از نور به درون منطقه تاریک راه پیدا کند . شکل نیم سایه هم به اندازه منبع نور گسترده و جسم حائل و فاصله آنها از همدیگر بستگی دارد  ,که سه حالت موجود می باشد . که بستگی به قطر زاویه ای چشمه نور و جسم حائل دارد 
شکل های شماره ۴ تا  ۶ این مطلب را به خوبی نشان می دهد .

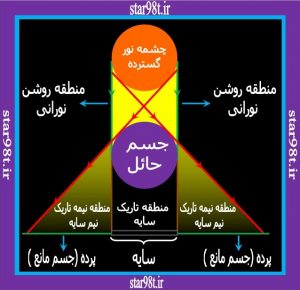
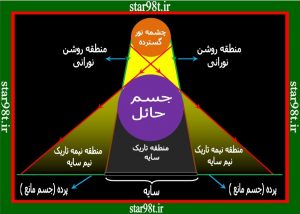
شکل شماره  ۴-  چشمه نور گسترده مخروط  کوچک شونده ایجاد می کند

شکل شماره ۵ – چشمه نور گسترده مخروط به موازات جسم حائل به پیش می رود

شکل شماره ۶ – چشمه نور گسترده مخروط بزرگ شونده ایجاد می کند

۴ – سایه زمین

در این قسمت در مورد سایه زمین که توسط خورشید ایجاد می شود و در فضا به دنبال  زمین کشیده می شود توضیح می دهیم .

۱) سایه زمین

زمین در حرکت خود بدور خورشید که یک سال طول می کشد, همواره نصف آن با نور خورشید روشن می شود و نصفه دیگر آن در تاریکی باقی می ماند (پدیده ای که ما به عنوان شب می شناسیم ) چون خورشید در هر زمان تنها نصف زمین را می تواند روشن کند .
همانند همه اجسامی که می بینیم در مقابل نور سایه ایجاد می کند کره زمین هم در مقابل خورشید سایه ایجاد می کند که به صورت یک مخروط به دنبال زمین خرکت می کند.این مخروط از شب زمین شروع شده و حداکثر تا ۰۰۰ر۳۸۰ر۱کیلومتر ادامه پیدا می کند ( ۱۰۸ برابر قطر زمین ) که البته این بستگی به فاصله زمین تا خورشید داشته و تا ۰۰۰ر۴۰کیلومتر می تواند کمتر باشد (۰۰۰ر۳۴۰ر۱تا ۰۰۰ر۳۸۰ر۱کیلومتر) از نظر نوع چشمه نور ,خورشید چشمه نور گسترده  است و یک مخروط کوچک شونده را برای زمین ایجاد می کند . ( شکل شماره  ۷ )

 

 شکل شماره ۷ – سایه زمین به دنبال زمین در فضا

 ۲) نیم سایه

همچنان که تمامی سایه های ایجاد شده توسط مخروط های کوچک شونده علاوه بر سایه نیم سایه هم دارند سایه زمین در فضا هم نیم سایه دارد که از الگوی شکل شماره ۴ تبعیت می کند( شکل شماره ۸ )

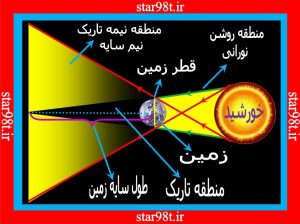
شکل شماره ۸ – سایه زمین

۳) طول و اندازه سایه زمین و پارامتر دلتا  

سایه ای که زمین در حرکتش به دور خورشید ایجاد می کند مخروطی دراز می باشد که قاعده آن قطر کره زمین و طول آن در حدود ۰۰۰ر۳۸۰ر۱ تا ۰۰۰ر۳۴۰ر۱ آنچه اهمیت دارد نسبت طول سایه زمین به قطر زمین می باشد که پارامتر دلتا می نامند(Δ)  . بنابر این دلتا(Δ) بین ۱۰۵تا ۱۰۸می باشد. هرچه زمین به خورشید نزدیکتر باشد (نقطه حضیض) مقدار(Δ) بیشتر و هرچه زمین ازخورشید دورتر باشد (Δ) کمتر می باشد. برای محاسبات این قسمت و قسمت های بعد , ما مقدار (Δ) را همان ۱۰۸در نظر می گیریم .   

در قسمت های بعد با استفاده از مقدار(Δ), فاصله زمین تا ماه همچنین  فاصله زمین تا خورشید را محاسبه خواهیم کرد . ولی قبل از آن راجع به قطر زاویه ای توضیح می دهیم .

۵ – قطر زاویه ای

در نجوم قطر اجسام را که در کره آسمان دیده می شود به قطر زاویه ای بیان می کنند و قطر واقعی در درجه بعد محاسبه می کنند . در این قسمت در مورد قطر زاویه ای و رابطه آن با قطر واقعی توضیح می دهیم .

۱) قطر زاویه ای

اگر از یک فاصله مشخص به یک جسم دور و یا نزدیک نگاه کنیم و مثلثی را در نظر بگیریم که یک راس آن چشمان ما باشد و دو راس دیگر آن دو سر جسمی که می بینیم . در آن صورت قطر زاویه ای,  زاویه راس سوم مثلث می باشد که در چشمان ما قرار دارد ( شکل شماره ۹ )
اندازه اجسام آنطور که از زمین دیده می شوند . مقداری از کره آسمان را اشغال می کند . اگر کره آسمان را کره ای کامل در نظر بگیریم ( کره آسمان کره ای است فرضی که ناظر همواره نصف بالائی آن را می بیند – مراجعه کنید به  کره آسمان و شرح پاره ای از اصطلاحات نجومی  ) قطر جسم مشاهده شده یک کمانی از دایره عظیمه کره آسمان می باشد که بایدبرحسب واحد های زاویه (ماننددرجه یا رادیان)بیان شود.
هرچه جسم بزرگتر و نزدیکتر باشد قطر زاویه ای آن بیشتر و هرچه جسم کوچکتر باشد قطر زاویه ای آن کوچکتر است .
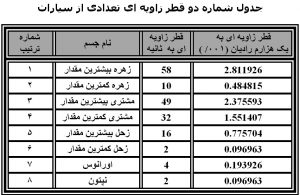
در جدول های شماره ۱ و ۲ می توانید قطر زاویه ای تعدادی از اجرام آسمانی را می توانید ببینید .با دقت در جدول مشاهده می شود که بیشترین قطر زاویه ای متعلق به ماه و خورشید می باشد که حدود ۵/ درجه قوسی می باشد (به یک درجه هم نمی رسد) و بعد قطر سیارات منظومه شمسی که همه آنها زیر یک دقیقه هستند و به ثانیه بیان می شود و بیشترین مقدار متعلق به زهره می باشد . قطر زاویه ای ستارگان بقدری کوچک است که همه آنها اجسام نقطه ای می باشند وبزرگترین قطر را شعرای یمانی دارد که ۰۰۷/ ثانیه قوسی می باشد . برای تبدیل قطر زاویه ای به قطر واقعی باید فاصله تا جسم مورد نظر را داشته باشیم . در قسمت بعد این موارد را محاسبه می کنیم .

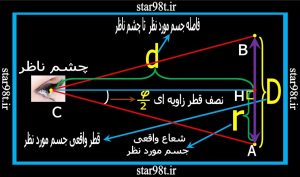
شکل شماره ۹ – قطر زاویه ای و رابطه آن با فاصله

۲) رابطه بین قطر زاویه ای و فاصله  

در شکل شماره ۹ داریم  :

بنابر این می توانیم بنویسیم : 

نکته : بزرگترین قطر زاویه ای متعلق به خورشید می باشد که مقدار بسیار کوچکی است . بقیه اجرام سماوی هم قطر زاویه ای بسیار کوچکی دارند.بنابر این در مورد اشیاء آسمانی همیشه می توانیم با دقت بسیار زیادی مقدار tan زاویه را برابر با زاویه (بر حسب رادیان ) در نظر بگیریم در صورتی که جسم بقدری نزدیک باشد (اشیاء معمولی روی زمین) که مقدار (∝) بزرگ باشد و نتوانیم تقریب بالا را بکار برویم می توانیم فرمول را به این صورت بنویسیم :

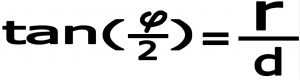
۳) جداول قطر زاویه ای اجسام آسمانی

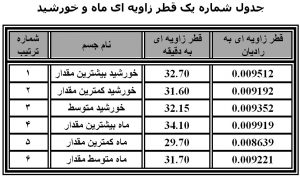
جدول های شماره یک و دو قطر زاویه ای ماه و خورشید را به دقیقه و رادیان نشان می دهد و جدول شماره ۲ قطر زاویه ای تعدادی از سیارات را به ثانیه نشان می دهد .
قطر زاویه ای شعرای یمانی (بزرگترین قطر در میان ستارگان ) فقط ۰۰۷/ ثانیه می باشد که اگر به رادیان حساب کنیم ۰۰۰۰۰۰۰۳۴/ رادیان می شود .

 

 ۶ – محاسبه دلتا

با دانستن فاصله زمین تا خورشید می توان مقدار (Δ) را بدست آورد و برعکس با اندازه گیری دقیق (Δ)  می توان فاصله زمین تا خورشید را بدست آورد.در اینجا محاسبات مربوطه به اندازه گیری دلتا را انجام می دهیم .

۱) محاسبه (Δ) از روی فاصله زمین تا خورشید

با توجه به شکل شماره ۱۰ داریم :

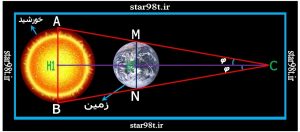
شکل شماره ۱۰ – محاسبه دلتا و فاصله زمین از خورشید

ابتدا مقادیر اولیه را می نویسیم :

حال با توجه به شکل  شماره ۱۰ می توانیم بنویسیم :

    

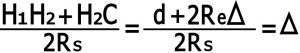
بنابر این می توانیم بنویسیم :

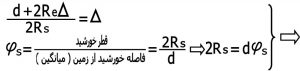
حال  می توانیم  فرمول را بر حسب (Δ) بدست حل کنیم که نتیجه می شود :

بدست آوردن دلتا بر حسب فاصله زمین تا خورشید

حال می توانیم با جاگزاری مقادیر معلوم , مقدار (Δ) را محاسبه کنیم  :
۱) قطر زاویه ای خورشید به دقیقه مقدار ۳۱٫۶ در نظر گرفته که این مقدار میانگین قطر زاویه ای می باشد .
۲) قطر زاویه ای را به رادیان تبدیل کرده و در فرمول فوق قرار می دهیم برای تبدیل دقیقه به درجه قطر زاویه ای را بر ۶۰ تقسیم می کنیم .
قبل از محاسبه باید ابتدا قطر زاویه ای خورشید را از دقیقه به درجه و بعد به رادیان تبدیل کند . برای تبدیل  درجه به رادیان از این فرمول استفاده می کنیم . ( برای دقت بیشتر مقدار عدد پی را ۳٫۱۴۱۶ در نظر بگیرید )

با جاگزاری مقادیر معلوم  می توانیم بنویسیم :               ۱۰۷٫۹۳۵ = Δ
نکته : در صورتی که ماشین حساب های پیشرفته و مهندسی در دست ندارید برای محاسبات خود می توانید با لینک زیر رفته و از ماشین حساب آنلاین استفاده کنید :  ماشین حساب آنلاین

۲)  محاسبه مقدار (Δ) برای اجسام کوچک   

در فرمول بالا اگر بجای زمین یک جسم دیگر قرار گیرد می خواهیم محاسبه کنیم مقدار (Δ) چه قدر می شود و یا به عبارت بهتر در روی زمین نسبت طول مخروط سایه ای که نور خورشید برای اجسام  ایجاد می کنند نسبت به قطر اجسام چقدر است؟ در اینجا بخاطر تمایز از (Δ) در اینجا این پارامتر را به طور ساده (Δa) می نامیم و بجای Re هم Da ( قطر جسم ) را قرار می دهیم :

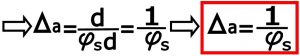
یعنی مقدار (Δa) برابر معکوس قطر زاویه ای خورشید است و این برای همه اشیاء مقداری ثابت است .
برای محاسبه  مقدار (Δa)  در مخرج کسر از مقدار Da  که در مقابلs d∝بسیار بسیار کوچک می باشد صرفه نظر کردیم ( s d= 1,400,000 km∝ ) در حالی که Da ابعادی در حدود متر و سانتیمتر دارد .

۳) محاسبه نسبت (Δ) با استفاده از (Δa)  

در واقع قطر زمین( ۱۲,۷۴۰Km )هم به اندازه  کافی در مقابل( s d= 1,400,000 km∝ ) کوچک است تا بتوانیم همین قاعده را هم در مورد (Δ) در نظر گرفته و مقدار (Δ) و (Δa) را برابر هم و برابر معکوس قطر زاویه ای خورشید بگیریم . ولی در جائی که به محاسبات دقیق تری نیاز داشته باشیم . باید مقدار دقیق (Δ) را بدست بیاوریم . بنابر این با توجه به فرمول های بدست آمده می توانیم بنویسیم :

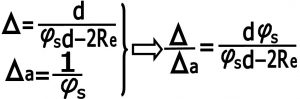
با جاگزاری مقادیر معلوم می توانیم بنویسیم :

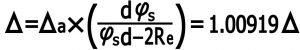
 ۴) اندازه گیری مستقیم (Δa)

مقدار (Δa) در روی زمین برابر است با نسبت طول مخروط سایه ای که خورشید برای اجسام بوجود می آورد به قطر اجسام , این پارامتر را می توان به راحتی با یک آزمایش اندازه گرفت . به این صورت که در موقع طلوع خورشید و یا موقعی که ارتفاع خورشید پائین است . یک توپ معمولی ( هرچه توپ بزرگتر باشد دقیق تر بدست می آید)در مقابل یک دیوار گرفته در این صورت سایه اش روی دیوار می افتد. توپ را بدقت و کم کم عقب برده تا سایه اش کوچک و کوچکتر شود ور لحظه ای که سایه توپ محو شد . فاصله توپ را از دیوار اندازه بگیرید . این فاصله قطر مخروط می باشد و با اندازه گیری قطرتوپ و همچنین قطر زاویه ای خورشید در موقع آزمایش براحتی می توان مقدار  (Δa) و به تبع  آن مقدار (Δ) را اندازه گرفت . ( شکل شماره ۱۱ )

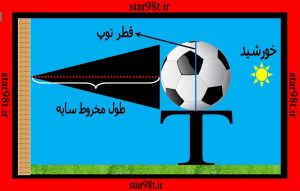
شکل شماره ۱۱ – روش مستقیم اندازه گیری دلتا

۷ – محاسبه فاصله زمین تا خورشید با استفاده از دلتا

در قسمت قبل با استفاده از فاصله ماه تا زمین به اندازه گیری (Δ) پرداختیم در این قسمت با استفاده از مقدار (Δ) فاصله زمین تا خورشید را محاسبه می کنیم .  

۱) اهمیت فاصله زمین تا خورشید و واحد نجومی

فاصله زمین تا خورشید یکی از مهمترین پارامترهای نجومی می باشد . در واقع همانند یک متر استاندارد در نجوم می باشد . از اندازه گیری فواصل اجرام نزدیک همانند ماه (البته اندازه گیری فاصله ماه تا زمین از روش های دیگر هم امکان پذیر است) تا سیارات منظومه شمسی و نزدیک ترین ستارگان و… دورترین کهکشان ها همه وابسته به اندازه گیری فاصله زمین تا خورشید می باشد . اهمیت فاصله زمین تا خورشید به حدی است که یکی از واحد های اندازه گیری فواصل بین سیارات  “واحد نجومی “ می باشد .
در فصل ها و بخش های آینده روش دقیق اندازه گیری فاصله زمین تا خورشید را ( اندازه گیری از روی گذر زهره ) شرح می دهیم در اینجا با استفاده از مقدار (Δ) این فاصله را اندازه گیری می کنیم .
واحد نجومی چیست : واحد نجومی که (به انگلیسی: astronomical unit) با نماد AU یا au نمایش داده می‌شود یکی از یکاهای طول است. متوسط فاصلهٔ زمین تا خورشید؛ که حدود ۱۵۰ میلیون کیلومتر یا ۹۳ میلیون مایل است، برابر با یک واحد نجومی در نظر گرفته شده‌است. ( مقدار دقیق آن ۱۴۹٬۵۹۷٬۸۷۰٬۷۰۰ متر می باشد)

۲) اندازه گیری فاصله زمین تا خورشید با استفاده از مقدار  (Δ)

در فرمول :

مقدار d را بر حسب (Δ)  بدست می آوریم . بنابر این داریم  :        

حال با استفاده از مقادیر معلوم همچون قطر زاویه ای ( بر حسب رادیان ) و  (Δ) و شعاع  زمین براحتی می توانیم فاصله زمین تا خورشید را بدست آوریم . در این مورد لازم است به نکات زیر توجه کنیم :
۱) برای تبدیل قطر زاویه ای به رادیان به عدد پی نیاز داریم که باید حداقل از ۴ رقم اعشار استفاده کنیم .
۲) باید مقدار (Δ) را با دقت بالا و در حدود حداقل ۴ رقم اعشار بدست آوریم . دقت کمتر از ۲ رقم میلون ها کیلومتر در اندازه گیری خطا ایجاد می کند .
۳) بدست آوردن مقدار دقیق (Δ) سخت ترین قسمت کار می باشد در واقع با روش هائی مانند روش اندازه گیری قطر مخروط سایه توپ مقدار (Δ) را نمی توانیم حتی با دقت متوسط تعیین کنیم و از این رو بدست آوردن مقدار d (فاصله زمین تا خورشید) از این راه بسیار سخت است . اگر چه از نظر تئوری ساده است .

۸ –  خسوف چگونه اتفاق می افتد ؟ ( ماه درون سایه زمین  )

سایه زمین به صورت مخروطی که قاعده اش قطر زمین را می سازد در فضا به دنبال زمین کشیده می شود . ماه در مدارش به دور زمین گاه گاهی از درون سایه زمین می گذرد در این حالت یا تمام و یا قسمتی از ماه ناپدید شده و یا به رنگ های :  نارنجی یا قرمز روشن و قرمز تیره و  آتشین دیده می شود .

۱) انواع خسوف

بسته به این که ماه چگونه از درون سایه زمین عبور کند انواع مختلف خسوف ( اتفاق می افتد ) شماره ۱۲ برای خسوف سه حالت در نظر می گیریم که خسوف کامل خود به دو حالت مختلف تقسیم می شود .
۱-۱) خسوف نیم سایه ای : در این نوع از خسوف ماه فقط از منطقه نیم سایه عبور می کند . مشاهده این نوع خسوف با چشم غیر مسلح بسیار مشکل می باشدزیرا تعغیر رنگ ماه بسیار اندک می باشد.( حالت۱)
حدود ۳۵ ٪ از خسوف ها خسوف نیم سایه ای هستند .
۲-۱) خسوف جزئی : در این حالت قسمتی ار قرص ماه از منطقه سایه عبور می کند و هرگز تمام قرص ماه از منطقه تمام سایه عبور نمی کند . با این حال قسمت عبور کرده محو شده و با چشم غیر مسلح براحتی دیده می شود . در این حالت سایه زمین هم روی ماه کاملا مشهود می باشد . ( حالت ۲)
حدود ۳۰ ٪ از خسوف ها خسوف جزئی هستند .
۳-۱) خسوف کامل :  در این نوع از خسوف قرص ماه تماما از منطقه سایه عبور می کند و بیشتر اوقات بجای محو شدن به رنگ های نارنجی مایل به قرمز تا قرمز تیره و جگری دیده می شود . در خسوف کامل گاهی مرکز ماه از مرکز سایه زمین می گذرد ( حالت ۳ ) که در این حالت زمان کسوف به حداکثر مقدار خود می رسد . و گاهی از بالا و پائين مرکز سایه زمین می گذرد که در این حالت زمان کسوف کامل کمتر می شود ( حالت ۴) 
حدود ۳۰٪ از خسوف ها کامل می باشند

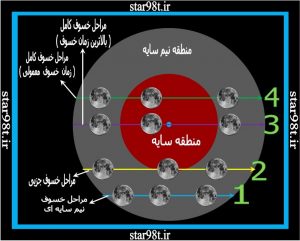
شکل شماره ۱۲ – انواع مختلف خسوف

 ۲) زمان های خسوف

زمان کل خسوف از لحظه ورود ماه به نیمسایه و بعد به تمام سایه در حالت های مختلف تفاوت های اساسی با هم دارد . بیشترین زمان مربوط به موقعی است که ماه در خسوف کامل بوده و مرکز ماه از مرکز سایه زمین می گذرد.فاصله ماه تازمین و فاصله زمین تاخورشید هم تاثیر زیادی درمدت زمان خسوف دارد.
از طرفی وقتی ماه نزدیکترین فاصله را با زمین داشته باشد,  قطر سایه زمین در محلی که ماه عبور می کند زیادتر بوده و ماه مسیر بیشتری را باید بپیماید . از طرف دیگر وقتی ماه نزدیکترین فاصله را با زمین داشته باشد در نقطه حضیض است و سرعت حرکت ماه بیشتر است و زودتر از سایه خارج می شود . همچنین وقتی ماه در دورترین فاصله باشد,  قطر سایه کمتر و در عوض سرعت حرکت ماه  هم کمتر است .
همچنین وقتی خورشید فاصله کمتری با زمین داشته باشد قطر سایه بیشتر می شود .
با درنظر گرفتن تمام این مواردحداکثر مدت زمان خسوف مربوط به زمانی می شودکه ماه از مرکز سایه بگذرد .
زمان های خسوف را می توانیم به این صورت طبقه بندی کنیم . و در یک رصد دقیق و علمی خسوف این زمان ها را یادداشت کنیم . ( شکل شماره ۱۳ )
۱) لحظه ورود ماه به تمام سایه t1 ( شروع گرفتگی )
۲) لحظه کامل شدن خسوف t2
۳) لحظه خروج ماه از تمام سایه t3 ( شروع باز شدن )
۴) لحظه خروج کامل ماه از تمام سایه t4 ( پایان کسوف )
البته زمان های ورود و خروج ماه به نیمسایه هم اهمیت خود را دارد ولی در اینجا به آن نمی پردازیم .
حال زمان های گرفت را از لحظه ورود ماه به تمام سایه در نظر گرفته و ببینیم حداکثر زمان گرفت چقدر است .
۱-۲) زمان وارد شدم قطر ماه در تمام سایه  :  از لحظه ورود ماه به تمام سایه تا لحظه کامل شدن خسوف یعنی (t2-t1) , که برابر است با لحظه شروع باز شدن ماه تا لحظه پایان خسوف تمام سایه (t4-t3) بنابر این :  t4-t3= t2-t1 این زمان حداکثر یک ساعت است .
۲-۲)زمان ورود نقطه ای در ماه به تمام سایه و خروج آن نقطه از  تمام سایه : گذشتن کامل ماه ازلحظه وارد شدن ماه به تمام سایه (شروع کسوف کلی) تا لحظه شروع به باز شدن ماه(t3-t1)  که این زمان برابر است با فاصله زمانی از لحظه کسوف کامل تا لحظه باز شدن کامل ماه ( پایان خسوف ) یعنی ( t4-t2 ( بنابر این : t3-t1= t4-t2 این زمان حداکثر ۲ساعت و ۴۴دقیقه می باشد .

    

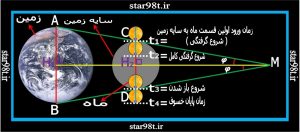
شکل شماره ۱۳ – زمان های ماه گرفتگی و تعیین فاصله ماه تا زمین

۳) مقابله و مقارنه چیست ؟

ماه در هر بار گردش به دور زمین موقعیتی پیش می آید که مراکز ماه و خورشید و زمین دقیقا در یک صفحه (نه لزوما در یک خط راست) قرار می گیرند دو حالت برای این موقعیت می توان در نظر گرفت .  
۱-۳) مقارنه : وقتی دو جسم به گونه ای کنار هم قرار می گیرند که ناظر زمینی آنها را در کنار هم می بیند به این حالت مقارنه می گویند آنچه در فضا اتفاق می افتد این است که مراکز زمین و دو جسم دیگر همزمان در یک صفحه واقع می شوند . بنابر این هنگامی که مراکز زمین و ماه و خورشید در یک صفحه واقع شوند می گویند مقارنه ماه و خورشید اتفاق افتاده است .

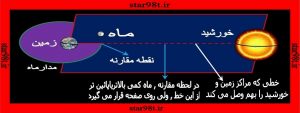
شکل شماره ۱۴- مقارنه ماه و خورشید

در مقارنه ماه و خورشید مراکز ماه و زمین و خورشید در یک صفحه قرار گرفته و ماه بین زمین و خورشید قرار می گیرد در روی زمین وقتی این حالت اتفاق می افتد ماه شب نو ( ماه پنهان و یا محاق ) می باشد و ماه در نزدیکی خورشید بوده و اگر مرکز ماه از یک حدی به خط واصل بین مراکز زمین و خرشید نزدیکتر شود کسوف ( خورشید گرفتگی ) جزئی یا کامل رخ می دهد . در این مورد در قسمت کسوف بیشتر توضیح می دهیم .
۲-۳) مقابله : مراکز ماه و زمین و خورشید در یک صفحه قرار گرفته ( نه لزوما در یک خط راست ) و زمین بین ماه و خورشید قرار می گیرد به این حالت مقابله می گویند.(شکل شماره ۱۵ )
در روی زمین ماه کامل ( بدر ) می باشد. در اینجا هم اگر مرکز ماه به خطی که مرکز زمین و خورشید را بهم وصل می کند از حدی نزدیکتر شود(۹/۵درجه)خسوف (کامل و ناقص و نیمسایه )قطعی می باشد .

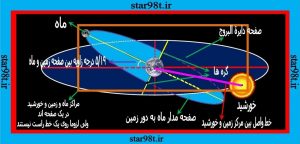
شکل شماره ۱۵ – مقابله ماه و خورشید

۴) خسوف چه موقع اتفاق می افتد ؟

در هر بار گردش ماه به دور زمین یک مقابله و یک مقارنه اتفاق می افتد یعنی مراکز ماه و زمین و خورشید در یک صفحه قرار می گیرد ولی لزوما خسوف( ماه گرفتگی) و کسوف (خورشید گرفتگی) اتفاق نمی افتد.زیرا برای خسوف و کسوف باید مرکز ماه هم تا حدودی به خطی که مرکز زمین و ماه را بهم وصل می کند نزدیک شود ( کافی است کمتر از ۹/۵درجه فاصله) و این امر در هر بار گردش ماه به دور زمین اتفاق نمی افتد .
دلیل آن این است که صفحه ای که در فضا مدار ماه را در بر می گیرد با صفحه ای که مدار زمین به دور خورشید (دایرۀ البروج) را در بر می گیرد بر هم منطبق نیستند و زاویه ۵/۱۹ درجه با هم می سازند . این امر موجب می شود که ماه گاهی از بالا و گاهی از پائین مخروط سایه زمین عبور کند و داخل مخروط(منطقه سایه و حتی نیم سایه ) قرار نگیرد (حداکثر ۳۲ کیلومتر از مخروط فاصله می گیرد ).بنابر این خسوف هم منتفی می شود .

۵) گره ها و خسوف

در واقع صفحه ای که مدار ماه به دور زمین را شامل می شود در دو نقطه دایره البروج را قطع می کند . که به این دو نقطه گره می گویند . یکی از گره ها را گره صعودی و یکی از گره ها را گره نزولی می گویند . وقتی مقابله ماه و خورشید اتفاق می افتد ( ماه کامل یا بدر ) ماه در قسمت های مختلفی در مدارش قرار می گیرد گاهی در روی گره ها ویا نزدیک گره ها و گاهی از گره ها فاصله می گیرد . موقعی شب بدر ( ماه شب کامل ) که به مقابله نزدیک می شویم اگر ماه به یکی از گره ها تا حدودی نزدیک باشد (و یا روی گره ها قرار بگیرد ) ماه داخل مخروط سایه شده و یکی از حالت های سه گانه خسوف (خسوف نیمسایه , خسوف ناقص و یا خسوف کامل ) اتفاق می افتد . (شکل های شماره ۱۶ و ۱۷ )

 

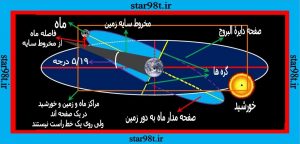
 شکل شماره ۱۶ – به زمان مقابله نزدیک شدیم ولی ماه از گره ها فاصله دارد  خسوف اتفاق نمی افتد

 

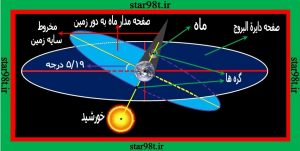
 شکل شماره ۱۷ – به زمان مقابله نزدیک شدیم  ماه در نزدیکی گره ها قرار دارد خسوف اتفاق می افتد 

 ۶) چرا ماه در موقع خسوف قرمز می شود ؟

اگر زمبن جو نداشت در هنگام خسوف ماه کاملا ناپدید می شد . ولی اتمسفر زمین قسمتی از نور خورشید را به ماه می رساند . نور خورشید از طیف های مختلفی تشکیل شده است (بنفش , آبی , سبز و…. قرمز ) نورهای آبی و بنفش که طول موج کوچکتری دارند پراکنده شده و این لاعث می شود ما آسمان را آبی ببینیم . ( نگاه کنید به آسمان و افق در ماه  – چرا آسمان آبی است ؟ ) ولی نورهای طیف قرمز و نارنجی از جو عبور کرده و همین نورها می باشند که در هنگام خسوف که در کره ماه قرص خورشید پوشیده شده به سطح ماه می رسند . علاوه بر این سطح ماه هم نورهای تابیده شده از جو زمین را تعغیر می دهد و در مجموع در هنگاه خسوف ماه به رنگ های مختلف از زرد و نارنجی و قرمز روشن و تیره تا مسی تعغیر می کند عوامل مختلفی در این امر دخیل هستند .
۱) شرایط جوی , آلودگی هوا , خاکستر حاصل از آتش سوزی جنگل ها و فوران آتشفشان ها و… می توانند رنگ نوری را که به سطح ماه برخورد می کند تعغیر دهند و بر درخشندگی رنگ ها تاثیر گزار باشند .
۲) سطح ماه هم رنگ های تابیده را تعغیر داده و بازتابش می کند و با توجه به عوارض ماه و جنس خاک در قسمت های مختلف ماه نور بازتابیده تعغیر کرده و در مجموع رنگ قسمت های مخلف تفاوت های جزئی باهمدیگر پیدا می کنند .
در مجموع همه عوامل فوق باعث ایجاد رنگ های مختلف شده که از یک خسوف تا خسوف دیگر تفاوت هائی با یکدیگر دارند .
حال فرض کنید در سطح ماه ایستاده اید وقتی زمین به طور کامل قرص ماه را پوشاند حلقه ای آتشین با رنگ های زرد تا قرمز (بستگی به خسوف دارد )دور قرص سیاه شده خورشید را می پوشاند و سطح ماه با نور نارنجی تا قرمز روشن می شود . 

۷) طبقه یندی خسوف بر اساس رنگ ماه

همانطور که گفته شد رنگ و درخشندگی ماه بستگی به میزان گرد و غباری دارد که در طی خسوف در اتمسفر زمین وجود دارد. بنابر این رنگ های مختلفی در یک خسوف نسبت به خسوف دیگر مشاهده می شود  دانژون دانشمند فرانسوی كسي بود كه بر اساس شدت تيرگي ماه از قرمز تند تا قرمز روشن را بين Lتا L4 تقسيم بندي نمود.
با استفاده از« میزان درخشندگی دانژون» برای ماه گرفتگی ، منجمان آماتور می توانند رنگ و درخشندگی ماه را طبقه بندی کنند.
۱)  بسیار تاریک:  در این حالت ماه تقریبا “غیر قابل مشاهده” است.
۲)تاریک : ماه به رنگ خاکستری یا قهوه ای دیده می شود.جزییات سطح ماه به سختی قابل تشخیص است.
۳) نسبتا” تاریک : یک لکه تیره درون قرص دیده می شود وکناره های قرص روشن تر دیده می شوند.
۴) سرخ آجری : گاهی نوری روشن یا زردی در کناره های قرص مشاهده می شود.
۵) رنگ مسی یا نارنجی- سرخ : قرص ماه روشن دیده می شود.
شکل شماره ۲۰  , ماه را نشان می دهد که در دو خسوف متفاوت وارد سایه زمین می شود .
در حالت اول ( خسوف A ) از قسمت بالاتر می گذرد و وارد منطقه پرتوهای قرمز می شود . ( شکل شماره ۱۹)
در حالت دوم ( خسوف B ) از قسمت پائین تر گذشته و وارد منطقه تاریکی می شود . ( شکل شماره ۲۰ )
در هر کدام آنچه از زمین و ماه دیده می شود به تصویر کشیده شده است .

 

 شکل شماره ۱۸ – ماه در حرکتش به سمت سایه زمین دو خسوف متفاوت خسوف A
( داخل پرتوهای قرمز ) خسوف B ( داخل منطقه تاریکی)

 

 شکل شماره ۱۹ – خسوف A ماه در حرکتش به سمت سایه زمین از منطقه پرتوهای قرمز می گذرد . آنچه در روی زمین و ماه دیده می شود

 

 شکل شماره ۲۰ – خسوف B ماه در حرکتش به سمت سایه زمین از منطقه تاریک می گذرد . آنچه در روی زمین و ماه دیده می شود

 

 ۹-اندازه گیری همزمان فاصله ماه تا زمین و قطر ماه با استفاده از روش آریستاخوس

یکی از فوائد خسوف این است که به هنگام خسوف می توان بسیاری از محاسبات نجومی از جمله اندازه گیری فاصله ماه تا زمین را انجام داد این کار پیشینه تاریخی دارد . در این قسمت به اندازه گیری فاصله ماه و قطر ماه در هنگام خسوف می پردازیم .

۱) آریستارخوس چه کسی بود ؟

آریستارخوس (به یونانی: Ἀρίσταρχος) (حدود ۳۱۰ تا ۲۳۰ ق. م) ستاره‌شناس و ریاضی‌دان یونانی برجسته در یونان باستان بود.

وی اولین دانشمند شناخته شده‌ای است که به الگوی سامانه خورشیدی و گردش زمین و سیاره‌های دیگر به دور خورشید باور داشت. اندیشه‌های او در دوران باستان طرفدار چندانی نیافت و جهان علم تا مدت‌ها از نظریهٔ مرکزیت زمین و کیهان‌شناسی بطلمیوسی پیروی می‌کرد. ۱۸۰۰ سال بعد کپرنیک ایدهٔ مرکزیت خورشید را دوباره مطرح کرد. آریستارخوس از اندیشه‌های فیلولائوس متأثر بود ولی سیاره‌ها را به ترتیب درستی بر پایهٔ فاصلهٔ آن‌ها در گرداگرد خورشید «آتش مرکزی» قرار داد. مانند آناکساگوراس او نیز باور داشت که: ستارگان هم شاید چیزهایی مانند خورشید باشند .
اولین اندازه گیری ها برای تعیین فاصله ماه تا زمین توسط او انجام شد . او توانست به کمک ماه گرفتگی و اندازه گیری زمان های گرفت فاصله ماه تا زمین را حدود۶۰برابر شعاع زمین اندازه گیری کند.که چیزی حدود ۰۰۰ر۳۸۶ کیلومتر شد.که در نوع خود بی نظیر بود . او همچنین پی برد که اندازه سایه زمین در محلی که ماه از آنجا عبور می کند بیش از ۲/۵ برابر قطر ماه می باشد .  

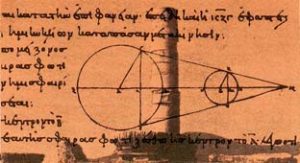
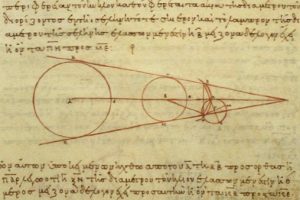
شکل های شماره ۲۱ و ۲۲ – یاد داشت های آریستارخوس در باره اندازه گیری فاصله ماه تا زمین

 

شکل شماره ۲۳ – آریستارخوس

۲) اندازه گیری فاصله ماه تا زمین به روش آریستارخوس

برای اندازه گیری فاصله ماه تا زمین به این صورت عمل می کنیم  :
۱-۲)  مقادیر معلوم : ابتدا مقادیر اولیه و معلوم را می نویسیم :

قبل از آن به  قسمت : “ ۷   – خسوف چگونه اتفاق می افتد ؟ ( ماه درون سایه زمین  ) “ – “۲) زمان های خسوف”  همچنین شکل شماره ۱۳  مراجعه می کنیم .

شکل شماره ۱۳ – مربوط به محاسبات این قسمت

۲-۲ ) مقادیر مجهول  : مقادیری  که باید اندازه گیری کنیم از این قرار است .

۳-۲) اندازه گیری قطر زاویه ای ماه و سایه زمین از روی زمان های کسوف :  دوره تناوب ماه یعنی مدت زمانی که طول می کشد ماه یک دور دور زمین بچرخد را با T نشان می دهیم که این مدت ۲۷/۳ روز ( ۷۰۸ ساعت ) است

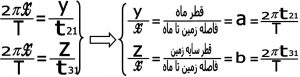
مقدار a  در این فرمول همان اندازه زاویه ای ماه ( بر حسب رادیان ) می باشد که می توان به صورت مستقیم با اندازه گیری قطر زاویه ای ماه تعیین کرد . و مقدار b هم اندازه زاویه ای  سایه زمین می باشد که آن هم می توان در موقع خسوف ناقص به طور مستقیم تعیین کرد ولی هدف ما در این قسمت اندازه گیری a و b با توجه به زمان های  خسوف می باشد .
مراجعه کنید به : “قسمت ۵ – قطر زاویه ای  “ – “۲) رابطه بین قطر زاویه ای و فاصله ”    همچنین شکل شماره ۹  

شکل شماره ۹ – مربوط به قطر زاویه ای

نکته : در بدست آوردن این تناسب مدار ماه به دور زمین را دایره در نظر گرفته  و سرعت حرکت ماه را در مدت خسوف ثابت فرض کردیم . دیگر این که مسیر حرکت ماه را در سایه زمین خط راست فرض کردیم .

۴-۲) تشابه مثلث ها : در شکل شماره ۱۳ مثلثABM  و  مثلث MCD متشابهند . بنابر این داریم :

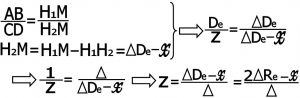
۵-۲) تشکیل سه معادبه و سه مجهول  : سر انجام  با توجه به معادلات نوشته شده دستگاه سه معادله و سه مجهول تشکیل می دهیم .

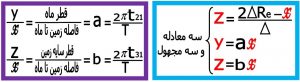
۶-۲) حل دستگاه سه معادله و سه مجهول : با حل سه معادله و سه مجهول مقادیر مجهول x و y و Z را بدست می آوریم.با توجه به حداکثر زمان خسوف که مربوط به گذر مرکز ماه از مرکز سایه زمین می باشدداریم

 با جاگزاری مقادیر معلوم در معادله ها داریم :

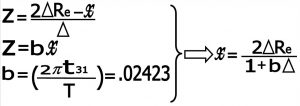
نکته : این اندازه گیری ها در صورتی صحیح است که مرکز ماه از مرکز سایه زمین بگذرد . که در آن صورت زمان های خسوف به حداکثر مقدار خود می رسد . پس رصد گر زمینی باید چندین خسوف کامل را رصد کند تا بتواند بالاترین زمان خسوف را بدست بیاورد , که همان هم به عوامل مختلفی مانند فاصله زمین از خورشید و فاصله ماه تا زمین بستگی دارد . با توجه به دامنه تعغیرات فاصله ماه تا زمین (از۳۵۶ تا ۴۰۵ هزار کیلومتر ) این مقدار با تقریب خوبی قابل قبول است .

۳) بقیه پارامترها

تا اینجای کار توانستیم فاصله ماه تا زمین را با تقریب بسیار خوبی بدست بیاوریم  
۱) قطر , سایه زمین در محل ماه گرفتگی :

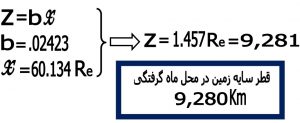
۲) قطر ماه  :

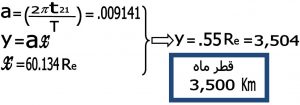
 ۳) اندازه مخروط سایه زمین :

با توجه به آن که در زمان  آریستارخوس  هنوز شعاع زمین بدرستی معلوم نشده بود اندازه گیری ها را بر اساس شعاع زمین تعیین کرد مثلا فاصله ماه تا زمین را ۶۰ برابر شعاع زمین محاسبه کرد . و مقدار دلتا را هم با آزمایش توپ توانست بدست بیاورد و زمان ها را هم از ساعت های شنی و ابزاری مشابه آن بدست می آوردند .

۱۰- اندازه گیری فاصله ماه تا زمین و قطر بوسیله سایه زمین در خسوف ناقص

در موقع خسوف ناقص سایه زمین قسمتی از ماه را می پوشاند و شکل سایه به صورت کامل و مشخص دیده می شود . این یکی از دلائلی بود که قدما به کروی بودن زمین پی بردند .
در این قسمت با استفاده از تصویر سایه زمین در روی ماه و بدست آوردن نسبت قطر سایه زمین به قطر ماه همان محاسبات قسمت قبل را کامل می کنیم .

۱) روش کلی محاسبه بدون اندازه گیری زمان های خسوف

تمام اندازه گیری هائی که در قسمت قبل ( قسمت ۸ ) انجام دادیم از روی زمان های خسوف بود . به کمک زمان های خسوف مقادیر a و b (قطر زاویه ای ماه و سایه زمین) را بدست آورده و بعد از روی آن xو yو z (فاصله ماه تا زمین , قطر ماه,  قطر سایه زمین)را بدست آوردیم در اینجا مقادیر a و b را مستقیم از روی نسبت قطر سایه زمین به فاصله ماه تا زمین (z/x) و همچنین نسبت قطر ماه به فاصله ماه تا زمین(y/x) بدست می آوریم. توجه کنید آنچه مستقیما اندازه گیری می کنیم نسبت ها می باشد.و بعد به کمک معادلاتی که در قسمت قبل بدست آوردیم . مقادیر  x و y و z را بدست می آوریم . بنابر این داریم (فرمول های قسمت قبل – قسمت ۸ ) :
  

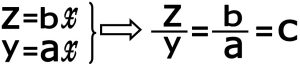
 نسبت محاسبه شده را c نامگزاری می کنیم بنابر این آنچه برای ما مهم است بدست آوردن مقدار c و a می باشد که در این صورت مقدار b هم بدست می آید و به طبع آن x و y و z را هم بدست می آوریم .
خوبی این روش در آن است که دیگر نیازی نیست منتظر خسوفی باشیم  که ماه از سایه زمین بگذرد ( خسوفی با بالاترین زمان های خسوف ) بلکه کافی است از یک خسوف ناقص عکس با کیفیت بالا گرفته و همان شب قطر زاویه ای ماه را با ابزارهای اندازه گیری زاویه اندازه بگیریم .

۲) بدست آوردن (b/a) از روی مشخص کردن مراکز دایره ها(قطر ماه و قطر سایه زمین) از عکس

همانطور که گفته شد در این روش باید یک عکس کیفیت بالا از خسوف ناقص بگیریم .

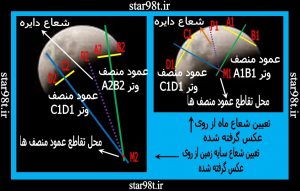
شکل شماره ۲۴ – تعیین مرکز ماه  ( اندازه گیری شعاع ) و مرکز سایه زمین ( اندازه گیری شعاع ) از روی عکس

به ترتیب این مراحل را دنبال می کنیم .( شکل شماره ۲۴ )
۱) رسم دو وتر روی عکس ماه :  در روی عکسی که از ماه تهیه کردیم دو وتر رسم می کنیم . ( وترهای A1B1 و D1C1 )
۲) عمود منصف وترها را رسم می کنیم :   عمود منصف خطی است که از وسط پاره خط  برآن عمود می شود .
۳) محل تقاطع عمود منصف ها را بدست می آوریم :  همچنان که روی شکل دیده می شود محل تقاطع عمود منصف ها مرکز دایره می باشد . بنابر این خطی که از محل تقاطع عمود منصف ها ( نقطه M ) به محیط دایره وصل شود شعاع دایره می باشد بنابر این M1P1 شعاع ماه می باشد و ۲M1P1 قطر ماه که می توانیم آن را با خط کش دقیق اندازه بگیریم .
۴)شعاع و قطر سایه ماه: به همین ترتیب شعاع(M2P2) قطرسایه زمین(۲M2P2)را هم بدست می آوریم .

حال با توجه به مقادیر بدست آمده داریم :

با توجه به اندازه گیری های انجام شده این مقدار  ۲/۶۵ می باشد ( شما می توانید خودتان این مقدار را اندازه بگیرید )

برای ادامه محاسبات به مقدار a هم نیاز داریم که این مقدار در واقع قطر زاویه ای ماه بر حسب رادیان می باشد . قطر زاویه ای ماه ‘۳۱٫۴۲ ( دقیقه ) می باشد که باید به رادیان تبدیل شود .

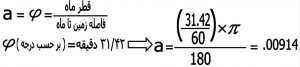
بنابر این مقدار b برابر است با :

با مشخص شدن a ( قطر زاویه ای ماه به رادیان ) و b( قطر زاویه ای سایه زمین به رادیان )مقادیرx ( فاصله زمین تا ماه ) و y ( قطر ماه ) و z ( قطر سایه زمین ) هم بدست می آید .

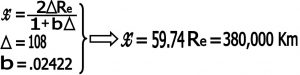
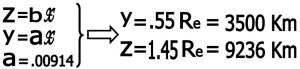
نکته : بهتر است برای سالم ماندن عکس چند کپی از عکس گرفته شده و روی کپی خط های حاصل را بکشیم ) بعد این مراحل را دنبال کنیم .

 ۳) روش اندازه گیری شعاع های ماه و سایه زمین در عکس با واژه پرداز Word

 می توانیم عکس گرفته شده را بدون چاپ کردن روی یک صفحه  Word آورده و بعد دایره ای رسم کنیم که ماه را بپوشاند و همچنین دایره ای که سایه زمین را بپوشاند و می توانیم قطر دایره ها را در همان Word پیدا کرده و نسبت (b/a) را از روی عکس تعیین کنیم ( شکل شماره ۲۵ )

شکل شماره ۲۵ – تعیین قطر ماه و قطر سایه زمین از روی عکس در واژه پرداز Word

 با این مقادیر بدست آمده و پس از جاگزاری داریم

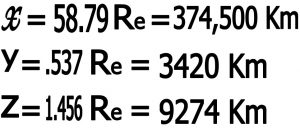
۴) نسبت زمان های خسوف (t21/t31)

  می توانیم با توجه به قسمت ۸  و تمام مطالب گفته شده تا اینجا بنویسیم :

 

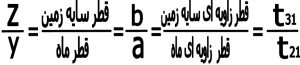
۱۰- قوانین خسوف و کسوف و پیش بینی و سایر مسائل مربوط به گرفتگی ها

نظر به این که خسوف و کسوف بسیار شبیه هم هستند و معمولا در یک مبحث بررسی می شوند ما قوانین و روش های پیش بینی را در قسمت کسوف مفصل شرح می دهیم در اینجا فقط  توضیح کوتاهی می دهیم .

۱) قوانین گرفتگی ها

همانطور که قبل از این هم اشاره شد . برای این که یک خسوف رخ دهد باید شرایط زیر باشد .
۱) ماه باید درحالت ماه بدر باشد این وضعیت هر ۲۹/۵روز یک بار تکرار می شود .
۲) ماه باید روی گره ها و یا نزدیک به گره ها باشد . این وضعیت هر ۳۴۶/۶۲ روز یک بار تکرار می شود .
تشریح کامل قوانین گرفتگی ها ( ماه گرفتگی و خورشید گرفتگی ) در بخش کسوف خواهد آمد .

جونپوری دانشمند هندی(متولد ۱۲۰۵تا ۱۲۷۳هجری شمسی) زاده جونپور (شمال هند) می باشد. او ریاضیدان و منجم هندی بوده و کتاب ها تالیفات فراوانی در نجوم و ریاضی از خود به یادگار گذاشت . از جمله کتاب جامع بهادر خانی که در نجوم وریاضیات است .
جونپوری در کتاب زیج بهادرخانی خود، شرایطی برای قابلیت مشاهده پذیری ماه گرفتگی ذکر کرده است. این شرایط عبارت اند از:
۱- به هنگام شب باشد یا از طلوع آفتاب بیش از ۲ ساعت و ۴ دقیقه نگذشته باشد یا به غروب آفتاب بیش از ۲ ساعت و ۴ دقیقه باقی نمانده باشد.
۲- ماه از گره‌ها بیش تر از ۱۲ درجه و ۲۸ دقیقه حرکت نکرده باشد.

۲) پیش بینی خسوف

پیش بینی خسوف به دو روش صورت می گیرد .
۱) از روی محاسبه دقیق مختصات ماه و خورشید
۲) از روی چرخه های ساروس که منجمان بابلی با پی گیری این چرخه ها می توانستند خسوف و کسوف را بدقت پیش بینی کنند . ( چرخه های ساروس دوره های حدود ۱۸ ساله هستند که یک کسوف یا خسوف دقیقا تکرار می شود )
توضیح کامل پیش بینی خسوف و کسوف و همچنین چرخه های ساروس دربخش کسوف تشریح خواهدشد .

۳) نماز آیات 

خسوف وکسوف از نظر مذهبی هم مهم است زیرا به واسطه آن نمازی به نام نمازآیات هم واجب می شود .
نماز آیات در این موارد واجب می شود .
۱) خسوف و کسوف هر چند کسی از آنها نترسد .
۲) زلزله بنابر احتیاط واجب اگر کسی نترسد هم باید خوانده شود .
۳) رعد و برق شدید و بادهای سرخ و سیاه فقط در صورتی که کسی بترسد .
برای آشناشدن به جزئیات به لینک زیر از دفتر آیت الله سیستانی مراجعه کنید .
نماز آیات ( از رساله حضرت آيت الله العظمي سیستانی )

برای مطالعه مقاله های روانشناسی اینجا  را کلیک کنید .

عکس های طبیعت, طبیعت خوانسار , شکوفه های بهاری  , گلستان کوه ,دانلود آلبوم های کامل بهترین و زیباترین عکس ها ,آلبوم هائی با صدها عکس کیفیت بالا ,  در هیچ کجای اینترنت این عکسها را پیدا نمیکنید , عکس هابدون استفاده از تکنیک های فتوشاپ تهیه شده , کاملا طبیعی 

برای آموزش کامل و حرفه ای گوگل مپ روی شکل زیر کلیک کنید

همه جیز در مورد گوگل مپ

۱) هر گونه اظهار نظر را در فرم اظهار نظر کاربران وارد کنید .
۲) نظرات بعد از تایید مدیریت نشان داده می شود .
۳) با انتقادات و پیشنهادات سازنده خود ما را هرچه بیشتر  همراهی کنید . مدیریت از انتقادات و پیشنهادات سازنده شما استقبال میکند .
۴) هرگونه بهره برداری : کپی تمام و یا قسمتی از مطالب این سایت بدون ارجاع منبع آن ممنوع می باشد .
۵) تکثیر فایل های Pdf با ذکر منبع آزاد ولی فروش آن تحت هر عنوان و با ذکر منبع هم ممنوع می باشد .