در این مقاله در مورد مقاطع مخروطی توضیح می دهیم . از چگونگی بوجود آمدن مقاطع مخروطی تا موارد استفاده از آنها و… توضیح می دهیم .
ولی قبل از آن توضیح کوتاهی در مورد بعضی از بخش های مختلف این مقاله می دهیم .
۱-تعریف و مقدمه ای بر مقاطع مخروطی و بخش های مختلف مقاله
در این بخش مطالب مختلفی که در بخش های مختلف این مقاله ذکر شده به طور بسیار مختصر معرفی شده است و توضیحات کاملتر در بخش مربوط ذکر شده است .
۱) مقاطع مخروطی چیست ؟
چهار شکل هندسی را به عنوان مقاطع مخروطی می شناسیم که عبارتند از : دایره ، بیضی ، سهمی و هذولی ( شکل شماره یک )
علت نامگذاری این اشکال به نام مقاطع مخروطی این است که این اشکال از برخورد یک صفحه با مخروط دوار تشکیل می شود که در بخش سوم به طور کامل توضیح می دهیم .
از آنجائی که بحث مقاطع مخروطی به صورت عمده به مخروط مربوط می شود و مخروط هم به هرم مربوط می شود قبل از مطالعه این بخش به مقاله های “ هرم “ و همچنین “ مخروط “ مراجعه کنید . همچنین لازم به یادآوری است که برای درک بهتر این مقاله و مقاله های در ارتباط با آن باید حداقلی از دانش و مهارت در سطح دیپلم متوسطه از ریاضیات و هندسه داشته باشید .
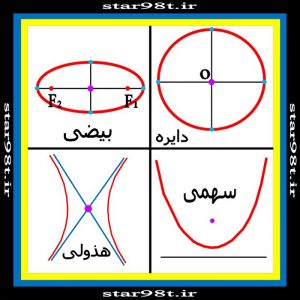
شکل شماره ۱ – مقاطع مخروطی : دایره ، بیضی ، سهمی و هذولی
۲) تعریف بر اساس مکان هندسی
همچنین مقاطع مخروطی را می توان بر اساس مکان هندسی نیز تعریف کرد. تعریف مکان هندسی و توضیح در مورد آن در بخش سوم به طور کامل توضیح داده می شود .
تعریف مقاطع مخروطی بر اساس مکان هندسی شامل یک تعریف نیست و هر کدام از اشکال چهار گانه تعریف های مختلفی دارند که در همان بخش سوم توضیح داده می شود .
۳) معادله مقاطه مخروطی
سیستم های مختصات در ریاضی و فیزیک و … نجوم و…علوم مختلف کاربرد های گسترده ای دارد فرمول های فیزیکی را به صورت معادلات جبری در آورده و با حل آنها بسیاری از پدیده ها را توضیح می دهند و …
نظر به اهمیت مقاطع مخروطی معادله مقاطع مخروطی یکی از مهمترین مباحث هندسه تحلیلی (دکارتی ) می باشد.(توضیح کاملتر هندسه دکارتی در مقاله “هندسه دکارتی“ در آینده منتشرخواهد شد داده می شود ) در بخش ششم توضیح مختصری در باره معادله مقاطع مخروطی می دهیم ولی بحث معادله مقاطع مخروطی و بزودی در مقاله “ معادله مقاطع مخروطی “ منتشر خواهد شد
۴) متناظر فضائی مقاطع مخروطی
مقاطع مخروطی که در اینجا ذکر می شود تنها اشکال دو بعدی هستند هر کدام از این اشکال متناظر سه بعدی هم دارند این اشکال عبارتند از : کره ( متناظر دایره ) ، کره گون ( شکلی بین کره و بیضی گون ) ، بیضی گون ، سهمی گون بیضوی( کاسه ای) ، سهمی گون هذولی وار (زین اسبی) ، هذولی گون یک پارچه و همچنین هذولی گون دو پارچه ( شکل شماره ۲) در مورد این اجرام در بخش ۷ توضیح می دهیم .
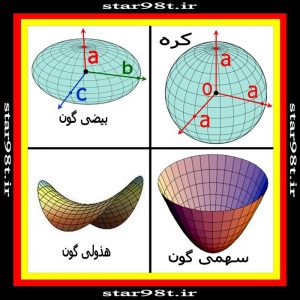
شکل شماره ۲ – کره ، بیضی گون ، سهمی گون کاسه ای و هذولی گون زین اسبی
۵) محیط و مساحت و حجم
در بین مقاطع مخروطی دایره و بیضی شکل های هندسی مسطح و سطح محدود می باشند بنابراین می شود برای آنها محیط و مساحت تعیین کرد . همچنین در مورد اشکال فضائی متناظر آنها مانند کره و کره گون و بیضی گون نیز وضع به همین ترتیب می باشد در بخش هشتم در موردمحیط و مساحت و حجم توضیحات مفصل تری می دهیم .
۶) هندسه های غیر اقلیدسی
تاکنون در هندسه از اصولی استفاده می کردیم که اقلیدس آن ها را درحدود ۳۰۰ سال پیش از میلاد مسیح برای اولین بار در کتاب “اصول” خود جمع آوری کرده بود. هندسه ای که اقلیدس در کتاب خود جمع آوری کرد به نام هندسه اقلیدسی نامیده می شود . این هندسه مخصوص فضای تخت می باشد ولی باید بدانیم بجز هندسه اقلیدسی انواع مختلفی از هندسه موجود می باشد که مخصوص فضای تخت نمی باشد این هندسه را هندسه نااقلیدسی می نامند . این هندسه ها به طور مستقیم به مقاطع مخروطی و متناظر فضائی آنها (کره ، بیضی گون ، سهمی گون و همچنین هذولی گون ) مربوط می شود در بخش نهم از همین مقاله به طور کامل در مورد آن توضیح داده شده است .
همچنین برای آشنائی با هندسه کروی می توانید به مقاله “هندسه های نا اقلیدسی و هندسه کروی “ از همین سایت مراجعه کنید .
۷) تاریخچه مقاطع مخروطی
تاریخچه مقاطع مخروطی یعنی تاریخچه بشر از شناخت مقاطع مخروطی ، نظر به اهمیت این موضوع در دو بخش مختلف ( بخش دهم تاریخچه مقاطع مخروطی در دوران باستان ) و بخش یازدهم ( تاریخچه مقاطع مخروطی در دوران اسلامی) به بررسی آن می پردازیم .
۸) استفاده از مقاطع مخروطی در علوم و تکنولوژی
دانش مقاطع مخروطی کاربردهای مختلفی در علوم و صنعت و تکنولوژی دارند و یکی از مهمترین دروس ریاضیات به حساب می آیند بنابراین ما در بخش دوازدهم به طور کامل در مورد استفاده از مقاطع مخروطی در علم و تکنولوژی توضیحات مفصل می دهیم .
۲- مخروط دوار
مخروط دوار شکلی است که از دوران یک خط حول خط دیگری در فضا بوجود می آید ولی قبل از پرداختن به موضوع مخروط دوار بهتر است ابتدا مخروط را تعریف کنیم .
۱) مخروط چیست ؟
مخروط یکی از شکل های هندسی می باشد که تعاریف مختلفی برای آن می توان کرد . از یک نظر مخروط را می توان نوعی هرم حساب کرد . هرم شکلی است که از وصل کردن تمام نقاط یک شکل مسطح (چند ضلعی و یا یک منحنی و…) به یک نقطه ثابت در فضا بدست می آید (برای توضیحات کاملتر در مورد هرم و انواع هرم و محاسبه حجم و … به مقاله “ هرم “ مراجعه کنید.) بنابر این مخروط را هم می توان نوعی هرم حساب کرد .
با این وجود می توان مخروط را هم مستقل از هرم تعریف کرد به این صورت که با دوران یک مثلث قائم الزاویه حول یکی از اضلاعش (بجز وتر) یک مخروط بدست می آید در این صورت ضلعی که دوران حول آن صورت گرفته ارتفاع و ضلع دیگر شعاع قاعده و وتر مثلث به یال مخروط تبدیل می شود . (برای توضیحات کاملتر در مورد مخروط و انواع مخروط و محاسبه حجم و مساحت مخروط و… به مقاله “ مخروط “ مراجعه کنید.)
نکته : در صورتی که مثلث قائم الزاویه حول وترش دوران کند دو مخروط کامل و عمودی که در قاعده مشترک و بهم چسبیده هستند بدست می آید .
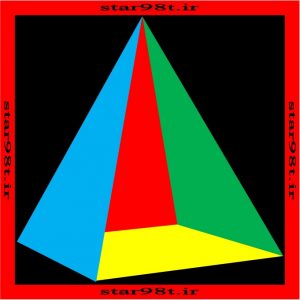
شکل شماره ۳ – هرم
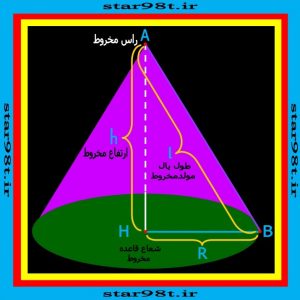
شکل شماره ۴ – مخروط معمولی
۲) مخروط دوار چگونه بدست می آید؟
در صورتی که یک مثلث قائم الزاویه حول یکی از اصلاعش دوران کند مخروط بدست می آید با حجم و مساحت جانبی مشخص ، ولی فرض کنیم دو خط متقاطع در فضا داشته باشیم و یکی از خطوط دور خط دیگر شروع به دوران کند در این صورت دو مخروط بی انتها بدست می آید که از طرف راس به هم چسبیده اند . خطی که دوران حول آن صورت گرفته خط محور مخروط و خطی که دوران کرده مولد مخروط نامیده می شود از آنجائی که این دو مخروط انتها ندارند حجم و قاعده و مساحت و مساحت جانبی نمی توان در مورد آن تعریف کرد .
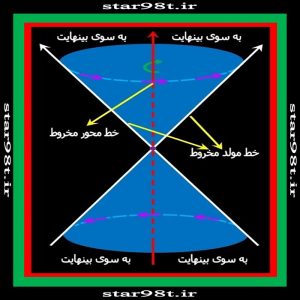
شکل شماره ۵ – مخروط دوار
۳- تقاطع یک صفحه با مخروط دوار
در این بخش مقاطع مخروطی را تعریف کرده و در مورد چگونگی تشکیل آن توضیح می دهیم .
در صورتی که یک مخروط دوار در فضا داشته باشیم و صفحه ای این مخروط را قطع کند بسته به این که چگونه و با چه زاویه ای مخروط را قطع کند شکل های مسطحی در صفحه پدید می آید که به آن مقاطع مخروطی می گویند. و ابتدا فقط توضیح کوتاهی راجع به این شکل ها می دهیم و بعد هر کدام را در یک بخش به طور مفصل بررسی می کنیم . ( شکل شماره ۶ )
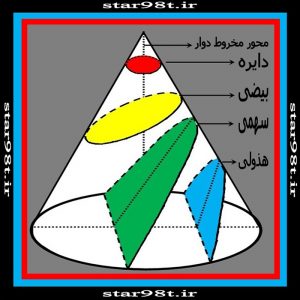
شکل شماره ۶ – کلیه مقاطع مخروطی
۱) خطوط مولد مخروط دوار
وقتی یک خط حول خط دیگری دوران پیدا کند مخروط دوار درست می شود در این صورت خط های بیشماری را در سطح مخروط دوار می توان در نظر گرفت که کاملا روی سطح مخروط دوار قرار گرفته و از راس مخروط می گذرند . این خطوط را می توان خطوط مولد(تولید کننده ) مخروط نامید . در حقیقت در ابتدا یک خط وجود داشت بر اثر دوران آن خط و بعد از ساخته شدن مخروط دوار بینهایت خط مولد تولید شد . ( شکل شماره ۷ )
نکته ۱: باید در نظر گرفت مخروط دوار دو بخش مجزا و کاملا شبیه هم دارد که یکی در بالا و یکی در پائینِ راس مشترک قرار دارد وقتی از مخروط دوار صحبت می کنیم در واقع هر دو بخش مخروط را مدنظر قرار می دهیم .
نکته ۲ : وقتی مخروط دوار را مورد بررسی قرار می دهیم دو بخش مخروط تا بینهایت گسترده شده و نمی توان آن را محدود دانست . در واقع مهمترین تفاوت مخروط دوار با مخروط معمولی در این است که مخروط دوار یک شکل نامحدود می باشد و بنابراین حجم و سطح جانبی نمی توان برای آن در نظر گرفت . این نکته در توضیح اشکالی مانند هذولی و سهمی که نامحدود هستند بسیار مهم می باشد .
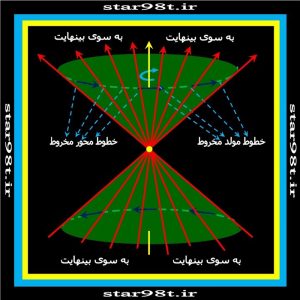
شکل شماره ۷ – خطوط مولد مخروط دوار
۲) دایره(Circle)
اگر یک صفحه عمود بر محور مخروط دوار (خطی که دوران حول آن صورت گرفته –شکلهای شماره ۸و ۹) مخروط را قطع کند فصل مشترک مخروط و صفحه یک منحنی بسته ای را تشکیل می دهد که دایره می نامیم.( تعریف دیگر دایره را در بخش چهار توضیح می دهیم ) اگر کسی روی یک دایره در یک جهت حرکت کند سرانجام به نقطه ای که شروع به حرکت کردیم برمی گردیم . از اینرو این شکلی مانند دایره را شکل بسته می نامیم .
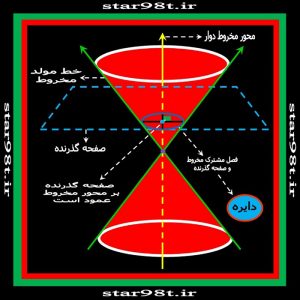
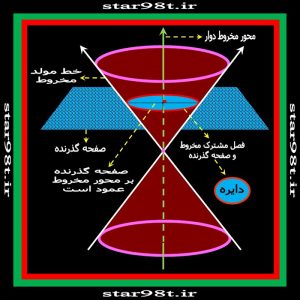
شکل های شماره ۸ و ۹ – صفحه عمود بر محور مخروط ، مخروط را قطع کرده است و تشکیل دایره داده است .
۳) بیضی (Ellipse)
حال فرض کنیم صفحه قطع کننده بر محور مخروط عمود نبوده ولی با هیچکدام از خطوط مولد هم موازی نباشد فصل مشترک مخروط و صفحه یک منحنی بسته ای را تشکیل می دهد که بیضی می نامیم ( تعریف دیگر بیضی را در بخش چهار توضیح می دهیم) اگر زاویه صفحه قاطع با محور مخروط اندکی کمتر از ۹۰درجه باشد بیضی نزدیک به دایره بدست می آید حال هرچه این زاویه از ۹۰درجه دورتر شود بیضی کشیده تر می شود . ( شکل های شماره ۱۰ و ۱۱) در بیضی هم چون یک شکل بسته است ( مانند دایره ) کسی که از یک نقطه در روی بیضی و در یک جهت شروع به حرکت کند سرانجام به محل اولش برمی گردد .
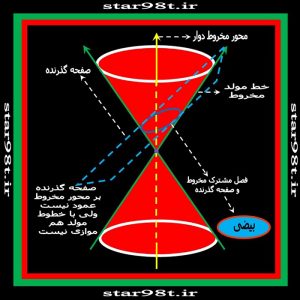
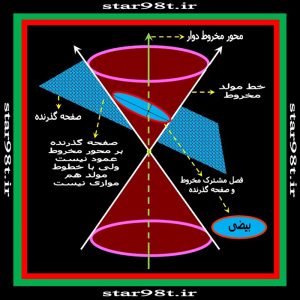
شکل های شماره ۱۰ و ۱۱ – صفحه قطع کننده به صورت مایل می باشد ولی هنوز موازی خطوط مولد مخروط نشده است و از این رو بیضی تشکیل داده است.
۴) سهمی (Parabola)
حال صفحه قطع کننده مخروط دوار که بر محور مخروط عمود نبوده بیضی تشکیل داده است . زاویه صفحه را باز هم از۹۰درجه دور تر می کنیم بیضی کشیده تر می شود ، باز هم دورتر باز هم بیضی کشیده تر و… تا جائی می رسد که صفحه قاطع با یکی از خطوط مولد موازی می شود . در این صورت دیگر سطح بسته ای به نام بیضی بدست نمی آید بلکه سطح بازی (سطح باز سطحی است که خطوط آن تا بینهایت گسترده شده و هرگز بهم نمی رسد تا شکل بسته و محدودی را درست کند) به نام سهمی بدست می آید ( تعریف دیگر سهمی را در بخش چهار توضیح می دهیم) سطحی که باز بوده به طوری که اگر کسی روی آن حرکت کند هرگز به جای اولش بر نمی گردد . ( شکل های شماره ۱۲ و ۱۳ )
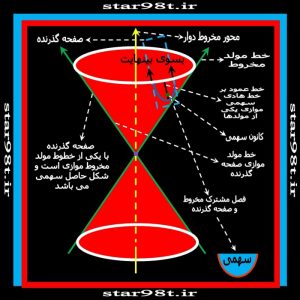

شکل های شماره ۱۲و ۱۳ – صفحه قطع کننده موازی یکی از خطوط مولد مخروط شده است از این رو سهمی تشکیل شده است.
۵) هذولی(Hyperbola)
وقتی که صفحه به موازات یکی ازخطوط مولد مخروط دوار را قطع کرد شکلی باز به نام سهمی بدست می آید. صفحه قاطع که فصل مشترک آن با مخروط دوار تشکیل سهمی را داده مخروط را در یک طرف قطع می کند . ولی اگر باز هم صفحه گذرنده را کج کنیم سهمی های مختلفی بدست می آید ولی هرگز صفحه قاطع مخروط را در دو طرف قطع نمی کند به علاوه دیگر سهمی فقط یک شاخه دارد .
اگر به کج کردن صفحه ادامه دهیم سرانجام صفحه با محور مخروط موازی می شود و در این صورت صفحه قاطع مخروط را در دو طرف راس قطع می کند و دو شکل باز بدست می آید که از نظر هندسی در واقع دو شاخه یک شکل هستند شکل جدید دیگر سهمی نیست بلکه هذولی نام دارد . ( تعریف دیگر هذولی را در بخش چهار توضیح می دهیم) در هذولی نیز مانند سهمی اگر کسی روی یکی از شاخه های هذولی حرکت کند هرگز به جای اولش بر نمی گردد .
مهمترین تفاوت هذولی با سهمی در این است که سهمی یک شاخه و در یک طرف مخروط دارد ولی هذولی دو شاخه و در دو طرف مخروط (دو طرف راس مخروط )دارد . (شکل شماره ۱۴ ) بنابراین هذولی شکلی باز با دو شاخه مجزا می باشد .
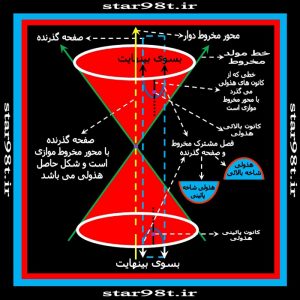
شکل شماره ۱۴ – صفحه قطع کننده موازی محور مخروط شده است از این رو هذولی تشکیل شده است به دو شاخه هذولی دقت کنید.
۶) خطوط متقاطع
صفحه ای که به موازات محور مخروط ، مخروط را قطع کند تشکیل هذولی می دهد حال هرچه این صفحه به محور مخروط نزدیکتر باشد دو شاخه هذولی بیشتر به هم نزدیک شده و انحنای هذولی کمتر می شود و بنابراین هذولی های مختلفی بدست می آید . حال صفحه باز هم به نزدیکتر شدن به محور مخروط ادامه داده تا سرانجام بر محور مخروط منطبق شود (محور مخروط جزئی از خطوط صفحه شود) در این صورت دیگر هذولی تشکیل نمی شود بلکه دو خط متقاطع بوجود می آید . ( شکل شماره ۱۵ )
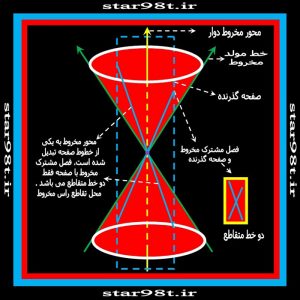
شکل شماره ۱۵- صفحه قطع کننده بر محور مخروط منطبق شده است از این رو تنها دو خط متقاطع تشکیل می شود .
۴- تعاریف و ویژگی های هندسی مقاطع مخروطی
در بخش قبلی توضیح دادیم که چگونه از برخورد یک صفحه با یک مخروط دوار شکل های مختلفی بوجود می آید( دایره ، بیضی ، سهمی و هذولی ) در اینجا در مورد تعریف این شکل های هندسی و ویژگی های آن توضیح کوتاهی می دهیم . ولی قبل از آن در مورد یک اصطلاح مهم در هندسه به نام مکان هندسی توضیح می دهیم .
۱) مکان هندسی
مجموعه نقاط بهم پیوسته ای را در نظر بگیرید که همه این نقاط دارای یک خاصیت هندسی مشترک باشند و بر عکس هر نقطه ای دارای این خاصیت باشد عضوی از این مجموعه نقاط باشد . این مجموعه نقاط را در هندسه “مکان هندسی” می گویند .
مکان هندسی در هندسه بسیار اهمیت دارد و بسیاری از مسائل هندسی را به این طریق می توان حل و فصل کرد برای نمونه می توان به این موارد اشاره کرد : مکان هندسی کلیه نقاطی که از دو سر سر پاره خط به یک فاصله باشند عمود منصف آن پاره خط نام دارد و یا مکان هندسی کلیه نقاطی که از دو ضلع یک زاویه به یک فاصله باشند نیمساز زاویه نام دارد و… در هندسه نمونه های بسیاری را می توان مثال زد که بوسیله مکان هندسی تعریف می شوند .
۲) دایره(Circle)
دایره تعاریف مختلفی دارد . دایره را همانظور که در بخش سوم شرح دادیم می توان از برخورد صفحه ای عمود بر محور یک مخروط بدست آورد (مخروط محدود و با انتها یا مخروط نامحدود بی انتها ) ولی تعاریف مختلفی را می توان برای دایره بر شمرد .
۱-۲) تعریف بر اساس مخروط : دایره شکلی است که از قطع کردن مخروط دوار توسط یک صفحه عمود بر محور مخروط تعریف می شود که در این مورد در بخش قبلی مفصل توضیح دادیم .
۲-۲) تعریف اقلیدسی : مکان هندسی کلیه نقاطی که از یک نقطه ثابت به نام مرکز به یک فاصله باشند دایره نامیده می شود . مطابق با این تعریف آن نقطه ثابت مرکز دایره حساب می شود . و فاصله نقاط روی دایره از مرکز شعاع دایره نامیده می شوند . ( دو برابر شعاع هم قطر نامیده می شود ) این تعریف از دایره تعریف اقلیدسی ( اقلیدس ریاضیدان بزرگ یونان باستان سده سوم قبل از میلاد و پدر علم هندسه) نامیده می شود .
بنابر این با توجه به شکل شماره ۱۶ داریم :
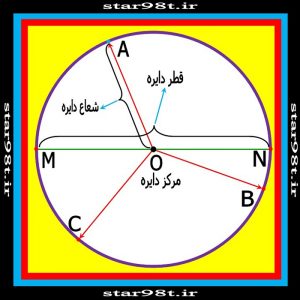
شکل شماره ۱۶- دایره و تعریف آن و قسمت های مختلف دایره و خواص آن

۳-۲) تعریف آپولونیوسی : آپولونیوس( ریاضیدان سده سوم پیش از میلاد که شهرت او به واسطه تحقیق در مقاطع مخروطی می باشد) نشان داد که دایره را میتوان به عنوان مکان هندسی همهٔ نقاطی نشان داده که نسبت فواصلشان از دو نقطهٔ ثابت عددی است ثابت و برابر است با نسبت فواصل دو نقطهٔ ثابت از دایره (شکل شماره ۱۷ )
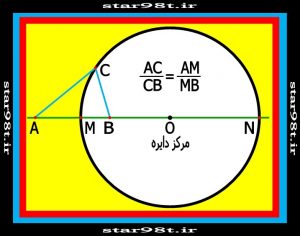
شکل شماره ۱۷ – تعریف آپولونیوسی دایره
نکته : می توان ثابت کرد که تعریف آپولونیوسی و اقلیدسی دایره معادل هم هستند .
۴-۲) دایره بی نهایت ضلعی منتظم : چند ضلعی های منتظم چند ضلعی هائی هستند که اندازه همه اضلاع و همه زوایا در آنها با هم مساوی هستند.حال هرچه تعداد ضلع های این چند ضلعی ها بیشتر شود چند ضلعی بیشتر به دایره میل می کند بنابراین دایره را می توان یک چند ضلعی با بی نهایت ضلع در نظر گرفت . ( شکل شماره ۱۸ )
شکل شماره ۱۸ – در یک چند ضلعی منتظم با افزایش تعداد اضلاع چند ضلعی به دایره نزدیکتر می شود.
۳) بیضی (Ellipse)
بیضی نیز تعاریف مختلفی دارد که در اینجا به طورخلاصه شرح می دهیم .
۱-۳) تعریف بر اساس مخروط : بیضی شکلی است که از قطع کردن مخروط دوار توسط یک صفحه به صورت مایل (و نه عمود) بر محور مخروط تعریف می شود که در این مورد در بخش قبلی مفصل توضیح دادیم .
۲-۳) تعریف بیضی با اعمال تجانس بر دایره : بیضی را میتوان به عنوان نتیجهٔ اعمال یک نگاشت خطی (تبدیل آفین) بر دایرهای به شعاع یک تعریف کرد. به دلیل پیچیده بودن این تعریف در اینجا در مورد آن توضیح دیگری نمی دهیم .
۳-۳) بیضی به عنوان مکان هندسی : بیضی مکان هندسی کلیه نقاطی است که مجموع فاصله آنها از دو نقطه ثابت مقداری ثابت است .که این دو نقطه را کانون بیضی می نامند و این مقدار ثابت برابر با قطر بزرگ بیضی است . ( شکل شماره ۱۹ )
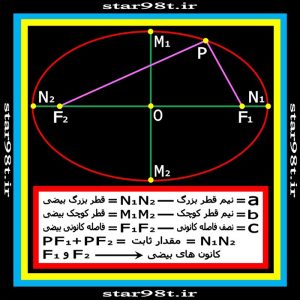
شکل شماره ۱۹ – بیضی و پارامتر های مربوط به بیضی (به نوشته های زیر شکل دقت کنید)
۳-۴) تعریف بر اساس خط هادی : بیضی را می توان مکان هندسی نقاطی تعریف کرد که نسبت فاصله اشان از یک نقطه (یکی از کانون های بیضی ) و یک خط راست (یکی از خطوط هادی) مقداری ثابت باشد . می توان ثابت کرد که این مقدار ثابت همان خروج از مرکز بیضی می باشد (تعریف دقیق تر خروج از مرکز در بخش بعدی تشریح خواهد شد ) شکل شماره ۲۰
نکته : همانطور که در شکل شماره ۲۰ مشخص شده نسبت فاصله هر نقطه از دو خط هادی (در دو طرف بیضی ) مشخص شده و این نسبت از طریق دو خط هادی اندازه گیری می شود که با هم برابر می باشند .
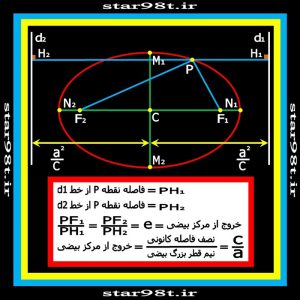
شکل شماره ۲۰ – بیضی و دو خط هادی آن و توضیحات مربوطه در زیر تصویر
۴) سهمی (Parabola)
سهمی نیز مانند دایره و بیضی تعریف های مختلفی دارد .
۱-۴) بر اساس مخروط : همانطور که گفته شد سهمی شکلی است که از برخورد صفحه ای به موازات یکی از خطوط مولد مخروط دوار پدید می آید و یک شکل غیر بسته و باز می باشد .
۲-۴) بر اساس مکان هندسی : سهمی ( شلجمی ) مکان هندسی نقاطی از صفحه است که از یک نقطه ثابت ( به نام کانون ) و یک خط ( خط هادی سهمی ) به یک فاصله است . ( فاصله هر نقطه به صورت جداگانه با کانون و خط هادی یکسان است ) (شکل شماره ۲۱ )
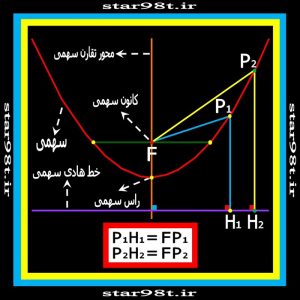
شکل شماره ۲۱ – سهمی و قسمت های مختلف آن
۵) هذولی (Hyperbola)
هذولی یکی دیگر از مقاطع مخروطی است که در مورد آن توضیح داده و تعاریف دیگر آن را نیز توضیح می دهیم .
۵-۱) بر اساس مخروط : همانطور که گفته شد هذولی شکلی است که از برخورد صفحه ای به موازات محور مخروط دوار پدید می آید و یک شکل غیر بسته و باز می باشد .
۵-۲) بر اساس مکان هندسی : هذولی مکان هندسی کلیه نقاطی است که اختلاف فاصله آنها از دو نقطه ثابت مقداری ثابت است .که این دو نقطه را کانون هذولی می نامند و این مقدار ثابت برابر با قطر بزرگ هذولی می باشد . ( تعریف قطرهای هذولی در شکل شماره ۲۳ مشحص شده است ) شکل های شماره ۲۲ و ۲۳
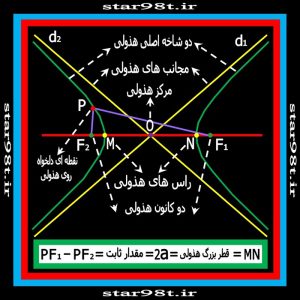
شکل شماره ۲۲ – هذولی و قسمت های اصلی آن
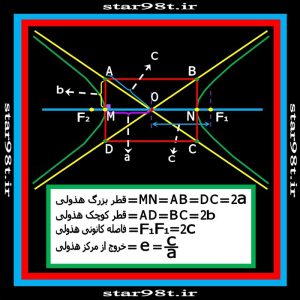
شکل شماره ۲۳ – مشخصات قسمت های مختلف هذولی
۵- خروج از مرکز
یک صفحه مخروط دوار را به طریق مختلف قطع می کند و شکل های مختلفی تشکیل می دهد در بخش های قبلی در این مورد به اندازه کافی توضیح دادیم . و بعد در مورد شکل های چهار گانه (دایره ، بیضی ، سهمی و هذولی) تعاریف و پارامترهای مختلفی را معرفی کردیم .یکی از این پارامترها که نه تنها نوع شکل بلکه چگونگی آن را هم مشخص می کند.خروج از مرکز یا برون مرکزی می باشد در واقع خروج از مرکز یک شکل انحراف آن شکل را از حالت دایره کامل مشخص می کند به گونه ای که اگر دو مقطع مخروطی خروج از مرکز برابر داشته باشند با یکدیگر متشابه هستند در این بخش خروج از مرکز را بررسی می کنیم .
۱) خروج از مرکز و خط هادی
خروج از مرکز یا برون مرکزی تعاریف مختلفی دارد و در واقع معیاری است که انحراف یک مقطع مخروطی را از حالت دایره بودن می سنجد .
هریک از مقاطع مخروطی میتوانند بدینگونه تعریف شوند : مکان هندسی نقاطی که فاصلهٔ آنها از یک نقطه (کانون) و یک خط (هادی) دارای نسبتی ثابت باشند. این نسبت، خروج از مرکز است و با e نمایش مییابد.
۲) تعریف خروج از مرکز بر اساس زاویه مولد مخروط دوار و صفحه قطع کننده
فرض کنیم یک مخروط دوار قائم را داریم که محورش بر سطح افق عمود است (سطح افق را به عنوان مبنا در نظر می گیریم ) و خطوط مولدش با سطح افق زاوبه “ آلفا “ را می سازد حال فرض کنیم یک صفحه با زاویه “بتا “نسبت به افق این مخروط را قطع می کند ( شکل شماره ۲۴ ) می خواهیم فقط با توجه به زاویه های “ آلفا “و “بتا “ فصل مشترک صفحه را با مخروط دوار بررسی کنیم که چه شکلی را می سازد . ( جدول شماره یک )
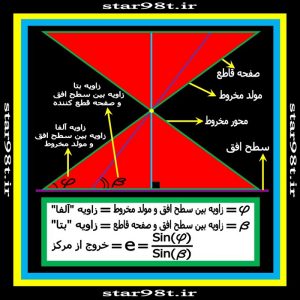
شکل شماره ۲۴ – مخروط دوار و زاویه خطوط مولد و همچنین صفحه قطع کننده با افق
جدول شماره یک : رابطه بین خروج از مرکز و شکل مقطع مخروطی
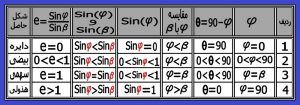
۳) فاصله کانونی و قطرهای مقاطع مخروطی
بین مقاطع مختلف مخروطی ، بیضی و هذولی دو کانون داشته و دایره و سهمی یک کانون (در مورد دایره این کانون مرکز نام دارد بنابر این فاصله کانونی دایره صفر است) دارند . فاصله کانونی را با “۲c” نشان می دهند و بنابراین “c” نصف فاصله کانونی می باشد ( شکل شماره ۲۳ )
علاوه بر این در مورد بیضی و هذولی قطر بزرگ و کوچک ( قطر کوچک و بزرگ دایره با هم مساوی و بنابراین دایره فقط یک قطر دارد ) قطر بزرگ بیضی و هذولی را با “۲b” نشان می دهند و قطر کوچک را با “۲a” بنابر این “b” و “a” به ترتیب نیم قطر بزرگ و نیم قطر کوچک نامیده می شود .
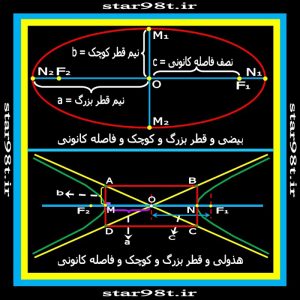
شکل شماره ۲۵ – نصف فاصله کانونی و نیم قطر بزرگ و کوچک بیضی و هذولی
۴) رابطه بین خروج از مرکز و قطر کوچک و قطر بزرگ و فاصله کانونی
با توجه به آنچه در مورد تعریف قطر بزرگ و کوچک و همچنین فاصله کانونی گفته شد و با توجه به شکل شماره ۲۵ می توان ثابت کرد که بین خروج از مرکز بیضی (و البته هذولی) و قطرهای بزرگ و کوچک این روابط برقرار است :
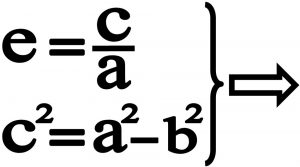

۵) خروج از مرکز دایره و سهمی
دایره یک کانون بیشتر ندارد بنابراین فاصله کانونی “۲c” در دایره صفر بوده و خروج از مرکز دایره صفر می باشد . بنابراین یک نوع دایره بیشتر نداشته و همه دایره های عالم با یکدیگر متشابه هستند .
در مورد سهمی هم با وجودی که یک کانون بیشتر ندارد ولی می توان ثابت کرد خروج از مرکز یک سهمی همیشه یک می باشد .
۶) خروج از مرکز بیضی و هذولی
خروج از مرکز بیضی بین صفر و یک می باشد هرچه خروج از مرکز بیضی به صفر نزدیکتر باشد فاصله کانونی کوچکتر و بیضی به دایره شبیه تر می شود و هرچه به یک نزدیکتر باشد بیضی کشیده تر و در حالتی که به یک برسد بیضی به سهمی تبدیل می شود . بنابراین با توجه به شباهت بیضی با دایره می توان دایره را هم نوعی خاص از بیضی حساب کرد که خروج از مرکز آن صفر شده است .
در مورد هذولی خروج از مرکز بزرگتر از یک می شود و با تعغیر خروج از مرکز هذولی های متفاوتی ساخته می شود .
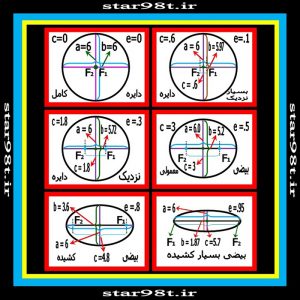
شکل شماره ۲۶ – با تعغیر خروج از مرکز بیضی از دایره کامل تا بیضی کاملا کشیده ساخته می شود .
۶- معادله مقاطع مخروطی
درفضای بیکران و یا روی یک صفحه مسطح و یا یک کره و یا حتی یک خط راست برای این که بتوان موقعیت یک مکان (نقطه ، شی و…) را تعیین کرد باید از سیستم مختصات استفاده کرد .
از طرفی هر شکلی (خط راست ، دایره ، بیضی و…) از تعداد نامتناهی نقطه تشکیل شده است . در دستگاه مختصات دکارتی (دو بعدی) هر نقطه با دو مختصات(x,y) تعریف می شود . در بسیاری از شکل ها یک یا چند رابطه جبری (معادله جبری ) بین x,y برقرار می باشد . به گونه ای که مختصات تمام نقاط واقع بر آن شکل در آن معادله یا معادلات صدق می کند. این معادلات جبری را معادله آن شکل در دستگاه محتصات دکارتی می نامند . در این بخش توضیحات کلی در مورد معادله مقاطع مخروطی داده ولی برای توضیحات کامل به مقاله “معادله مقاطع مخروطی “ مراجعه کنید .
۱) معادله کانونیک و گسترده مقاطع مخروطی در سیستم دکارتی
معادلات مقاطع مخروطی را در سیستم به دو صورت معادله کانونیک و معادله گسترده ( معادله ضمنی) می نویسند . ( برای آشنائی با سیستم مختصات دکارتی و سیستم های دیگر مختصات به مقاله “ مختصات در ریاضیات “ مراجعه کنید )
۱-۱) معادله کانونیک مقاطع مخروطی : معادله ای است که در آن پارامترهای مقاطع مخروطی (قطر ها و خطوط هادی و مرکز و یا راس مقطع مخروطی ) را بتوان از آن بدست آورد . در مقاله “معادله مقاطع مخروطی “ نشان می دهیم که چگونه می توان این معادلات را مستقیما از تعریف مقاطع مخروطی بدست آورد .
۱-۲) معادله گسترده : معادله ای است که به صورت کلی معادلات درجه دوم نوشته می شود .
۲) تبدیل معادلات کانونیک به گسترده و برعکس
معادلات کانونیک مقاطع مخروطی را مستقیما می توان از روی پارامترهای مقاطع مخروطی بدست آورد . و این معادلات کانونیک با انجام عملیات ساده ای به معادله گسترده تبدیل کرد و همچنین می توان معادلات گسترده را از طریق عملیات جبری به معادله کانونیک تبدیل کرد اهمیت این قسمت بیشتر در آن است که با تبدیل معادلات گسترده به معادلات کانونیک می توان پارامترهای لازم را از آن استخراج کرد . در مقاله “معادله مقاطع مخروطی “ نشان می دهیم که چگونه می توان معادلات گسترده را به معادلات کانونیک تبدیل کرد .
۳) معادلات مقاطع مخروطی در سیستم قطبی
در یک صفحه می توانیم بجای دو محور عمود برهم فقط یک محور در نظر بگیریم و مختصات یک نقطه را به جای فاصله از دو محور فاصله از مبدا و زاویه ای که پاره خط بین “ آن نقطه و مبدا “ با محور در جهت خلاف عقربه های ساعت می سازد ملاک قرار دهیم به این معادلات معادله قطبی می گویند .
۴) اهمیت معادلات مقاطع مخروطی
دانش مقاطع مخروطی کاربردهای مختلفی در علوم و صنعت و تکنولوژی دارند و یکی از مهمترین دروس ریاضیات به حساب می آیند . از ساخت لوازم و … مهندسی گرفته تا دانش فیزیک و نجوم (حرکت سیارات و… ) که در بخش دهم (۱۲- استفاده از مقاطع مخروطی در علوم و تکنولوژی) در چنین مواردی ( مانند حرکت سیارات و… ) مسیر حرکت به صورت معادله یکی از مقاطع مخروطی می شود و می توان روی آن مطالعه کرد .
۷- متناظر فضائی مقاطع مخروطی
دایره ، بیضی ، سهمی و هذولی شکل های دو بعدی هستند که در فضای سه بعدی هم متناظرهائی دارند که بعضی از این شکل ها از دوران مقاطع مخروطی حول قطر و یا محور آنها بوجود می آید . این اشکال سه بعدی می باشند . در این بخش در مورد این اشکال توضیح می دهیم .
۱) کُره (Sphere)
کره یک جسم سه بعدی و کاملا متقارن می باشد به گونه ای که هیچکدام از قسمت های ان نسبت به قیمت های دیگر برتری و ارجعیتی ندارد . تمام نقاطی که در سطح کره قرا دارند فاصله یکسانی از مرکز کره دارند که شعاع کره نامیده می شود . بیشترین فاصله دو نقطه در روی سطح کره پاره خطی است که از درون کره گذشته و همچنین مرکز کره هم بگذرد . و دو نقطه از کره را به هم وصل می کند که این پاره خط قطر کره نام دارد و دو برابر شعاع کره می باشد . هر صفحه ای که در فضای سه بعدی کره را قطع کند فصل مشترک آن با کره یک دایره می باشد .
در واقع کره را می توان شکلی دانست که از دوران دایره حول یکی از اقطارش بدست می آید .
بی شک کره یکی از ساده ترین و متقارن ترین و فراوانترین اشکال هندسی موجود در جهان می باشد کامل ترین نوع نظم و بیشترین تنوع، همگی در یک کره جمع شده اند . از زمینی که بر روی آن زندگی می کنیم تا ستارگان و سیارات گرفته تا … بسیاری از اجسام همه کره می باشند( در واقع شبیه کره هستند ) تحت تاثیر نیروی کشش سطحی و در غیاب گرانش همه قطرات مایع به شکل کره در می آیند .
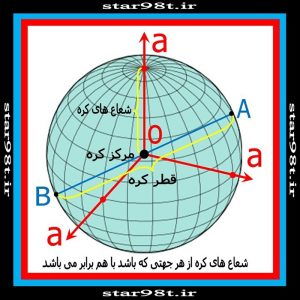
شکل شماره ۲۷ – کره و پارامترهای آن
۲) بیضی گون (Ellipsoid)
بیضی گون متناظر بیضی در فضای سه بعدی می باشد . بر خلاف کره که همه شعاع ها در هر راستائی مانند هم می باشد در بیضی گون همه شعاع ها (پاره خط هائی که مرکز بیضی گون را به سطح آن وصل می کند) با هم مساوی نیستند و بنابر این قطرهای بیضی گون هم مساوی هم نیستند . بیضی گون سه محور مختلف دارد که در سه راستای مختلف و عمود بر هم در مرکز بیضی گون به هم می رسند . و در حالت کلی با هم مساوی نیستند ( اگر مساوی باشند نام های دیگری به خود می گیرند ) هر صفحه ای که بیضی گون را قطع کند سطح مقطع یک بیضی می شود . بهترین مثال در مورد بیضی گون همان تخم مرغ می باشد .
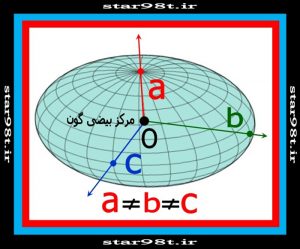
شکل شماره ۲۸ – بیضی گون و پارامترهای آن
۳) کره گون(Spheroid)
در حالی که بیضی گون از سه محور (سه قطر) با اندازه های گوناگون تشکیل شده است . کره گون نوعی بیضی گون می باشد که از سه محور دو محور آن هم اندازه هستند . و یک محور با دیگری فرق دارد .
کره گون را می توان شکل حاصل از دوران یک بیضی حول یکی از اقطارش بدست آورد . در حالی که بیضی گون از دوران هیچ شکلی بدست نمی آید .
۱-۳) کره گون دراز : اگر بیضی حول قطر بزرگش دوران کند کره گون دراز بدست می آید . ( توپ راگبی )
۲-۳) کره گون پهن : اگر بیضی حول قطر کوچکش دوران کند کره گون مسطح بدست می آید .
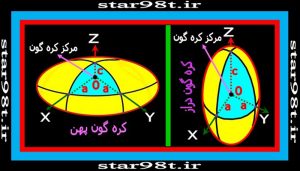
شکل شماره ۲۹ – انواع کره گون
۴) کره کامل و کره گونی و بیضی گون
در واقع کره کامل و کره گون را می توان حالت های خاصی از بیضی گون در نظر گرفت اگر مرکز بیضی گون را نقطه “O” بنامیم و سه محور عمود بر هم در مرکز بیضی گون در نظر یگیریم . و فاصله محل تقاطع محورها با سطح بیضی گون را تا مرکز بیضی گون را “a” و “b” و “c” بگیریم سه حالت وجود دارد .
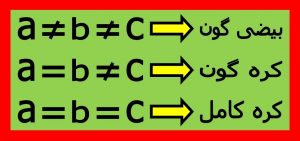
۵) کره کامل وجود ندارد
واقعیت این است که در دنیای واقعی کره کامل وجود ندارد .(حتی کره گون هم وجود ندارد) هر جسمی (چه طبیعی و چه مصنوعی مانند: ستارگان و سیارات و…تا توپ فوتبال و…) که ما آن را کره کامل می پنداریم تفاوت هر چند ناچیز بین قطرهای کوچک و بزرگ آن وجود دارد و این کافی است تا ازنظر هندسی دیگر کره به حساب نیاید. بنابراین اگر چه از نظر فیزیکی در نظر ما آنها کره کامل هستند ولی از نظر هندسی کره کامل نیستند و همگی بیضی گون به حساب می آیند . آنچه برای ما مهم می باشد نزدیکی با کره کامل می باشد .
به عنوان مثال ما زمین را یک کره کامل حساب می کنیم ولی باید بدانیم بین قطر استوائی زمین(۱۲۷۵۲ کیلومتر) و قطر قطبی زمین (قطری که از دو قطب میگذرد و۱۲۷۱۴کیلومتراست) ۳۸کیلومتر اختلاف وجود دارد ( ۳/ درصد) . با این وجود کره زمین از هر توپ و کره ای (توپ استاندارد فوتبال و والیبال و…) گردتر است . سایر سیارات و کرات آسمانی نیز وضعیت مشابهی دارند . خورشید کمترین اختلاف را بین قطر قطبی و استوائی خود دارد و گرد ترین جسم منظومه شمسی سایر ستارگان هم از سیارات به مراتب گردترند .
۶) رویه های درجه دوم
رویه های درجه دوم رویه هائی هستند که در سیستم مختصات دکارتی معادله آنها نسبت به سه مجهول (x,y,z) از درجه دوم باشد . رویه در فضا در واقع شبیه یک شکل دو بعدی در صفحه است بنابر این صفحه ای است خمیده معادله ای هم که نوشته می شود تنها مربوط به پوسته این صفحه می باشد ( سطح روی شکل با ضخامت صفر) در مورد معادله های این اشیا در سیستم دکارتی سه بعدی در آینده توضیح می دهیم . در اینجا تنها به این رویه ها اشاره می کنیم . این رویه ها عبارتند از :
۶-۱) گروه اول ، استوانه ( سطح مقطع بیضی یا دایره ) و مخروط دوار : در مورد مخروط دوار در بخش دوم همین مقاله توضیح داده و در مورد استوانه هم در آینده توضیح خواهیم داد .
۲- ۶) گروه دوم ، بیضی گون ، کره گون و کره : در مورد این رویه هادر قسمت قبل توضیحات کافی دادیم .
یکی از شباهت های این رویه ها به یکدیگر قرار گرفتن در گروه بیضی گون ها و دیگر داشتن سطح محدود است بنابراین ما آنها را به صورت یک شی سه بعدی در فضا می بینیم .
۶-۳) گروه سوم ، سهمی و هذولی گون ها : در مورد این رویه ها در قسمت بعدی توضیح می دهیم . شباهت این گروه این است که سطحی نامحدود داشته و ما تمام آنها را به صورت یک جسم نمی بینیم .
۷) سهمی و هذولی گون ها
رویه هائی هستند که متناطر سه بعدی سهمی و هذولی در فضای سه بعدی می باشند . و به چند گروه
تقسیم می شوند و در اینجا در مورد آنها توضیحات مختصری می دهیم .
۷-۱) سهمی گون بیضوی : سطحی است که در اثر گردش جسم سهمی بهدور محورش تشکیل میشود. شکل ظاهری آن (در صورتی که بالای آن توسط صفحه ای قطع شده باشد شبیه یک کاسه می باشد ) نمونه آن آینه های مقعر می باشد .

شکل شماره ۳۰ – سهمی گون کاسه ای
۷-۲) سهمی گون هذولی وار : نوع دیگر سهمی گون وجود دارد که شکل آن بر خلاف نوع اول به صورت کاسه نبوده و به صورت زین اسب می باشد از این رو سهمی گون زین اسبی هم نامیده می شود . نمونه دیگر این شکل چیپس خوراکی می باشد .

شکل شماره ۳۱ – سهمی گون زین اسبی
۷-۳) هذولی گون یک پارچه : بر اثر گردش یک هذولی و انتهای مخروط دواری که هذولی را تشکیل داده حول محورش بوجود می آید. ( چیزی شبیه قرقره خیاطی )

شکل شماره ۳۲ – هذولی گون یک پارچه
۷-۴) هذولی گون دو پارچه : بر اثر گردش فقط یک جسم هذولی حول محورش دو رویه در دو سوی مخالف هم بوجود می آید .

شکل شماره ۳۳ – هذولی گون دو پارچه
۸- محیط و مساحت و حجم
سهمی و هذولی یک شکل نامحدود و باز هستند بنابراین محیط و مساحت در مورد آنها نمی توان تعیین کرد ولی اگر همین سهمی یا هذولی را با یک (در مورد سهمی ) و یا دو خط قطع کرد محیط و مساحت محدود به شکل و خط را نیز می توان تعیین کرد همچنین متناظرهای سه بعدی هم که دارای سطح جانبی و حجم هستند می توان در مورد حجم و سطح کل آنها بررسی کرد در این صورت شکل هائی که در فضا بسته هستند دارای حجم و سطح جانبی می باشند ( کره و بیضی گون و کره گون ) ولی انواع سهمی گون ها و هذولی گون ها شکل های بازی هستند و نمی توان حجم و سطح جانبی در مورد آنها تعیین کرد . در این بخش فقط فرمول های مربوط به مساحت و محیط و سطح جانبی و سطح کل و حجم را می آوریم . ولی قبل از آن در مورد یک ثابت بسیار مهم در ریاضیات توضیح بدهیم .
۱) عدد پی
در ریاضی می توان اثبات کرد که نسبت محیط دایره به قطر آن عدد ثابتی به نام عدد “π ” ( عدد پی ) می باشد . این به آن معنی است که نسبت محیط دایره به قطر آن عددی ثابت می باشد و این به قطر و اندازه دایره بستگی ندارد یعنی دایره چه کوچک و چه بزرگ باشد نسبت محیط به قطر آن همیشه عددی ثابت به نام “عدد پی “ می باشد .(در مورد عدد پی یک مقاله مفصل به نام “ عدد پی “ در اینده توضیح خواهیم داد )
“عدد پی “ یکی ار ثابت های بسیار مهم در ریاضیات می باشد . بدون دانستن این عدد تمام پیشرفت های بشر ( در زمینه صنعت و تکنولوژی و علوم پایه و… ) غیر ممکن می شد از این رو روز ۱۴مارس ( برج سوم میلادی به نشانه رقم قبل از ممیز و روز ۱۴ بخاطر رقم بعد از ممیز ) مطابق با ۲۳ اسفند به عنوان روز جهانی عدد پی نامگزاری شده است .
عدد پی گنگ بوده یعنی تعداد رقم های بعد از اعشار آن نامحدود بوده و هیچ الگوی تکراری مشخصی هم ندارد فرمول های زیادی برای بدست آوردن عدد پی موجود می باشد که در اینجا به آن نمی پردازیم . مقدار آن با دو رقم اعشار ( که در بیشتر محاسبات بیشتر نیاز نیست ) تقریبا برابر است با ۳٫۱۴ = Π

۲) محیط و مساحت دایره
همانطور که در قسمت قبل گفته شد نسبت محیط دایره به قطر آن عددی ثابت به نام “عدد پی “ می باشد بنابراین محیط دایره برابر است با حاصل ضرب قطر در عدد پی ، مساحت دایره هم برابر است با مربع شعاع ضربدر عدد پی

نکته ۱: با توجه به محیط دایره مساحت دایره با روش انتگرال گیری از محیط دایره قابل اثبات می باشد.
۳) محیط و مساحت بیضی
تمام شعاع های دایره برابر هستند ولی بیضی دو قطر دارد با این حال فرمول مساحت بیضی شبیه دایره می باشد بنابراین بجای مجذور شعاع نیم قطرهای بیضی را که شبیه شعاع های دایره هستند در فرمول قرار می دهیم .

ولی برای مساحت بیضی فرمول خاصی وجود ندارد و فرمول هائی که تاکنون بدست آمده همه تفریبی هستند یکی از فرمول های مهم فرمول اویلر است :

۴) حجم و مساحت کره
مساحت و حجم کره از فرمول های زیر بدست می آید : ( اثبات این فرمول ها هم با روش انتگرال گیری اثبات می شود )

۵) حجم و مساحت بیضی گون و کره گون
فرمول های حجم بیضی گون و کره گون هم شبیه حجم کره می باشد و به این صورت است ولی برای مساحت فرمول دقیقی ارائه نشده است فرمول های مربوط به مساحت تقریبی بوده و ما در اینجا آنها را ارائه نمی کنیم .

۹- هندسه های غیر اقلیدسی
تاکنون در هندسه از اصولی استفاده می کردیم که اقلیدس آن ها را درحدود ۳۰۰ سال پیش از میلاد مسیح برای اولین بار در کتاب “اصول” خود جمع آوری کرده بود. این هندسه را هندسه تخت یا اقلیدسی می نامیم هندسه اقلیدسی در حدود ۲۰۰ سال پیش توسط دو ریاضیدان به نام “گاوس” و “ریمان” مورد بازنگری قرار گرفت و هندسه های دیگری بوجود آمد که اصل پنجم اقلیدس دیگر در آن صدق نمی کرد . (سایر اصول صدق می کردند ) این هندسه ها را هندسه های غیر اقلیدسی می نامند و از آنجا که این هندسه ها به مقاطع مخروطی مربوط می شوند در اینجا توضیح کوتاهی راجع به آن می دهیم .
برای مطالعه کامل به مقاله “هندسه های نا اقلیدسی و هندسه کروی” از همین سایت مراجعه کنید .
۱) هندسه اقلیدسی و غیر اقلیدسی
هندسه اقلیدسی و اصول آن در روی سطوح تخت کاربرد دارد ولی آیا همه سطوح تخت هستند؟ به عنوان مثال ما در روی کره زمین زندگی می کنیم که تخت نیست و کروی می باشد . و می توانیم نشان دهیم که هندسه اقلیدسی در روی سطح کروی (یا بیضوی) تفاوت فاحشی با هندسه تخت دارد همچنین می توانیم سطحی به شکل هذولی در نظر گرفته و نشان دهیم که اصول هندسه در روی این سطح هم با اصول هندسه در روی سطح تخت و کروی با هم متفاوت هستند (به عنوان مثال در هندسه کروی از هر نقطه خارج هر خط هیچ خطی نمی توان به موازات آن رسم کرد) از آنجائی که دایره حالت خاصی از بیضی و همچنین کره هم حالت خاصی از بیضی گون می باشد بجای هندسه کروی می توانیم هندسه بیضوی را به کار ببریم بنابراین سه نوع هندسه داریم . هندسه تخت ، هندسه بیضوی و هندسه هذولی
۲) هندسه هذولی (Hyperbolic)
هندسه هذولی یکی از هندسه های غیر اقلیدسی می باشد که تفاوت فاحشی با هندسه تخت و هندسه بیضوی دارد . به عنوان مثال در این هندسه از هر نقطه خارج هر خط بی نهایت خط راست می توان رسم کرد در این نوع هندسه فاصله خطوط در اصل توازی افزایش می یابد از این رو نام علمی آن (Hyperbolic) از کلمه یونانی هیپربالئین به معنی افزایش یافته گرفته شده است.در مورد این نوع هندسه درآینده توضیح خواهیم داد.
۳) هندسه بیضوی
هندسه بیضوی نوع دیگری از هندسه می باشد که با هر دو هندسه دیگر ( تخت و هذولی ) تفاوت دارد از آنجائی که کره نیز حالت خاصی از بیضی گون می باشد هندسه کروی هم حالت خاصی از هندسه بیضوی می باشد در مورد هندسه کروی هم در مقاله “ هندسه های نا اقلیدسی و هندسه کروی” توضیح کافی دادیم که برای مطالعه می توانید به آن مقاله مراجعه کنید .
۴) جمع بندی سه نوع هندسه
در شکل شماره ۳۴ و همچنین جدول شماره ۲ این تفاوت ها را می توانید ببینید .
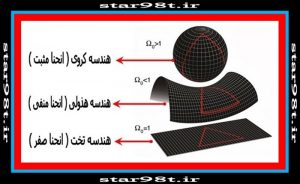
شکل شماره ۳۴ – تفاوت سه نوع هندسه
جدول شماره ۲- تفاوت سه نوع هندسه

۱۰- تاریخچه مقاطع مخروطی در دوران باستان
مقاطع مخروطی کاربرد بسیار زیادی در علوم و تکنولوژی دارد.شناخت مقاطع مخروطی از زمان یونان باستان با کتاب مخروطات آپولونیوس (در حدود ۲۰۰ قبل از میلاد) شروع شد .
۱) مقاطع مخروطی در دوران باستان
مقاطع مخروطی از زمان یونانیان باستان شناخته شده بود . کارهائی که ریاضیدانان یونان روی مقاطع مخروطی انجام دادن در دوران های بعد راهنمای کارهای دانشمندان و ریاضیدانان مختلف بود البته ریاضیدانان یونان باستان استفاده عملی از مقاطع مخروطی در علوم پایه (فیزیک و نجوم و…) نمی کردند ولی تحقیقات و اکتشافات زیادی در این زمینه انجام دادند . به عنوان مثال به عدد پی می توان اشاره کرد که روش علمی اندازه گیری عدد پی را به ارشمیدس نسبت می دهند چون اولین اندازه گیری ها را ارشمیدس انجام داد . به نام ثابت ارشمیدس هم نامیده می شود .
۲) اولین فرمول عدد پی توسط ارشمیدس
ارشمیدس دانشمند و ریاضیدان یونانی در سال ۲۷۸ قبل از میلاد در شهر سیراکوز یونان چشم به جهان گشود و در جوانی برای آموختن دانش به اسکندریه رفت. بیشتر دوران زندگیاش را در زادگاهش گذراند و با فرمانروای این شهر دوستی نزدیک داشت. او اکتشافات زیادی داشت که مهمترین کشف او در فیزیک به نام قانون ارشمیدس می باشد .
در زمینه ریاضی یکی از مهمترین کشفیات او بدست آوردن عدد پی”pi” می باشد.در آن زمان ”pi”نزد ریاضیدانان یونان شناخته شده بود آنها ”pi” را به طریق تجربی بدست آورده بودند ولی فرمولی علمی نتوانستند ارائه دهند.ارشمیدس نه تنها توانست اولین فرمول را برای ”pi” ارائه دهد (روش ارشمیدس
برای محاسبه ”pi” در مقاله “ عدد پی “در آینده به طور مفصل شرح داده خواهد شد) بلکه به طریق ریاضی ثابت کرد نسبت محیط دایره به قطر آن عددی ثابت است .
بعد از تصرف سیراکوز توسط رومیان در سال۲۱۲ قبل از میلاد ارشمیدس توسط یک سرباز مست رومی در کنار دریا کشته شد .

شکل شماره ۳۵ – ارشمیدس
۳) اقدامات آپولونیوس
آپولونیوس ریاضیدان یونانی در سال ۲۶۲ ق. م در شهر پرگا در آسیای صغیر (ساحل جنوبی ترکیه امروزی) در زمان سلطنت بطلمیوس به دنیا آمدو علم و دانش را در موزیوم فرا گرفت . او کارهائی را که اقلیدس و ارشمیدس کرده بودند تکمیل کرد . اگر چه مقام علمی آپولونیوس را کمتر از اقلیدس و ارشمیدس می دانند ولی مهمترین کار آپولونیوس کار روی مقاطع مخروطی می باشد بنابراین او را بحق پدر مقاطع مخروطی می نامند . او در کتاب خود به نام “مخروطات آپولونیوس “ برای اولین بار از تشکیل مخروط دوار و مقاطع مخروطی
(دایره ، بیضی ، سهمی و هذولی ) نام برد و خواص آنها را تشریح کرد .
آپولونيوس به طور کامل اين منحنى ها را مورد تحقيق قرار داد و حاصل کارهاى خود را در مجموعه اى متشکل از هشت کتاب ارائه کرد. اگر چه در زمان خود او پی به اهمیت کارش نبردند ولی بعدها اهمیت کار او آشکار شد . او در سال ۱۹۰ قبل از میلاد وفات کرد .

شکل شماره ۳۶ – آپولونیوس
۱۱- تاریخچه مقاطع مخروطی در دوران اسلامی
کاری که آپولونیوس شروع کرد در زمان خودش و زمان های بعد جدی گرفته نشد چون هیچ کاربرد عملی برای آن یافت نشد از این رو ادامه پیدا نکرد اوضاع چنین بود تا در دوران اسلامی به کوشش دانشمندان و ریاضیدانان ایرانی با ترجمه کتاب آپولونیوس دوباره از سر گرفته شد و ادامه پیدا کرد . در این بخش در مورد ادامه کار آپولونیوس توسط دانشمندان دوران اسلامی توضیح می دهیم .
۱) نهضت ترجمه
بعد از حمله اعراب به ایران تا مدت ها خلفای عرب تنها به فکر جهانگشائی و قتل و غارت و…بودند و از علوم مختلف اثری دیده نمی شد . بسیاری از آثار تاریخی و علمی نابود شده بودند و…
از زمان منصور عباسی بخاطر نیاز خلفا به علوم مختلف بخصوص علم پزشکی و بعدها نجوم توجه ویژه ای به این علوم شد و از آنجائی که اعراب گنجینه با ارزشی از این علوم نداشتند به همت وتشویق وزرا و اندیشمندان ایرانی توجه ویژه ای به ترجمه آثار ملل دیگر ( ایران و یونان و روم و هند و…)شد و تعداد زیادی کتب مختلف به زبان عربی ترجمه شد. دانشمندان ایرانی به ترجمه اکتفا نکردند و خود بر این گنجینه های علمی افزودند و دورانی را پدید آوردند که به دوران طلائی تاریخ اسلام معروف است . این نهضت که از زمان منصور عباسی شروع شد و در دوران هارون الرشید و مامون به اوج خود رسید به نام نهضت ترجمه معروف است .
۲) موسی بن شاکر خراسانی
زندگینامه موسی بن شاکر خراسانی در هاله ای از ابهام قرار دارد . به نقلی که چندان معتبر نیست او ابتدا راهزن بوده و بعد توبه کرده و به کسب علم و دانش و معرفت پرداخت . و منجم دربار مامون شد و خدمات با ارزشی به علم نجوم کرد .وی آثار علمی ارزندهای از خود بر جای نهاد .
۳) برادران بنوموسی
پسران “موسی بن شاکر خراسانی “ به نام های ( به ترتیب سن : حسن و احمد و محمد) که در قرن نهم میلادی می زیستند ( قرن سوم هجری ) در تاریخ علم به نام “برادران بنوموسی” نام گرفتند( آنها به به اخوان ثلاثه هم معروف هستند) آنها راه پدر را در علم و دانش ادامه دادند چون در دربار مامون عباسی صاحب نفوذ و ثروت فراوان شدند با این ثروت به کار ترجمه آثار یونانی و رومی و… پرداختند . و هم زمان تحقیقات علمی خود را در زمینه های مختلف علمی ( بخصوص ریاضی ) دنبال می کردند . آنها با هزینه شخصی افرادی را استخدام کرده و به سرزمین های مختلف (یونان و روم)برای تهیه کتب مختلف علمی می فرستادند وبا دادن دستمزدهای گاه گزاف به مترجمان حرفه ای کتاب ها را ترجمه می کردند . بنابراین خدمات فراوانی به علم کردند .

شکل شماره ۳۷ – برادران بنوموسی
شکل شماره ۳۸ – کتاب ” المخروطات ” برادران بنوموسی
۴) مشکلات ترجمه کتاب مخروطات آپولونیوس
یکی از کتاب های باارزشی که برادران بنوموسی ترجمه کردند کتاب “مخروطات آپولونیوس “ بود ولی ترجمه این کتاب به این راحتی نبود و آنها مشکلات متعددی در این راه داشتند عمده این مشکلات را به این صورت می توان خلاصه کرد .
۱-۴) نسخه بی کیفیت : برادران بنوموسی تنها نسخه ای که از مخروطات آپولونیوس در دست داشتند یک نسخه بی کیفیت بود که بسیاری از شکل ها و نوشته ها محو شده و به سختی خوانده می شد .
۱-۴) فراموش شدن بحث مقاطع مخروطی : در زمان برادران بنوموسی علم مقاطع مخروطی و کارهائی که آپولونیوس کرده بود و کتاب های او به فراموشی سپرده شده بود چون از همان زمان هم دانشمندان هیچ کاربرد عملی برای این تحقیقات پیدا نکردند و ارزش علمی هم برای آن قائل نبودند بلکه بیشتر آن را نوعی ورزش فکری می دانستند . از این رو روزی که برادران بنوموسی ترجمه “مخروطات آپولونیوس” را شروع کردند کسی نبود که در درک و فهم مطالب نوشته شده آنها را یاری دهد و از هیچکس نتوانستند کمک بگیرند .
۳-۴) همه مقاله های آن موجود نبود : کتاب آپولونیوس از هشت مقاله تشکیل شده بود که یکی از مقاله های آن را نداشتند و همین کار ترجمه را مشکل می کرد .
۴-۴) مشکل در خواندن متون یونانی : برادران بنوموسی به زبان یونانی مسلط بودند ولی هنوز هم در خواندن متون یونانی مشکل داشتند و این کار را سخت تر و پیچیده تر می کرد .
۵) چگونه برادران بنوموسی توانستند کتاب مخروطات آپولونیوس را ترجمه کنند ؟
بنا به آنچه گفته شد کار ترجمه کتاب به سختی پیش می رفت . مدتی بعد از شروع ترجمه حسن بن موسی ( برادر بزرگتر ) خودش نظریه مقاطع استوانه را وضع کرد که هم درک و فهم آن راحت تر بود و هم مقدمه ای شد بر کتاب اصلی بعد از فوت حسن ، احمد ( برادر وسطی ) بر حسب شانس توانست یک نسخه با کیفیت در سوریه پیدا کند که تنها چهار مقاله اول در آن موجود بود . به کمک این نسخه و مقاله ای که حسن در باب مقاطع استوانه ای نوشته شده بود . احمد و محمد سرانجام توانستند مطلب را کمال و تمام درک کنند . آنها ترجمه مقاله اول تا چهارم را به مترجم نامدار عرب به “هلال بن آب یهلال حمص “ و مقاله های پنجم تا هفتم را به مترجم دیگری به نام “ثابت بن قره” سپردند و تنها به کار آنها نظارت کرده و نسخه نهائی را تهیه کردند و نام آن را “ المخروطات “ گذاشتند و در نسخه های متعددی تکثیر کردند . لازم به ذکر است که نسخه پنجم مخروطات آپولونیوس یکی از سخت ترین و درخشان ترین آثار یونانی در زمینه ریاضیات می باشد .
۶) سایر کارهای برادران بنوموسی
برادران بنوموسی فقط هندسه دان نبودند بلکه آثار متعددی هم در علوم دیگر از خود برجای گذاشتند . برادر بزرگتر حسن در هندسه استاد تمام و کامل بود و بزرگترین هندسه دان زمان خودش بود او از کتاب های اقلیدس تنها نیمی از آن را خوانده بود ولی مسائلی را درک می کرد و قضیه هائی را طرح و ثابت می کرد که قبل از او هیچکس نتوانسته بود آنها را حل کند . محمد علاوه بر هندسه نجوم را هم خوب می دانست و در این زمینه استاد زمان خود بود ولی احمد به مکانیک علاقه داشت و تخصص او مکانیک بود . کوشش او صرف اختراع و ساخت دستگاه هائی شد که بدون دخالت انسان بتواند مدت های مدیدی کار کند . اگر این دستگاه ها ساخته می شد و به کار گرفته می شد انقلاب صنعتی و تکنولوژی مدرن از همان زمان آغاز می شود . او ۱۰۰ دستگاه مختلف را با شکل و توضیحات کافی( کارکرد و … جزئیات ) ارائه کرد ۲۵ تای آنها از آثار دانشمندان یونان می باشد و بقیه ( ۷۵ عدد ) از اختراعات او می باشد . که شرح و جزئیات این اختراعات در این مقاله نمی گنجد .
۷) ادامه کارهای برادران بن موسی و مطالعه و گسترش دانش مقاطع مخروطی
بعد از برادران بنوموسی ریاضیدانان و دانشمندان زیادی راه آنها را ادامه دادند و به تدریج موارد استفاده عملی از مقاطع مخروطی را هم پبدا کردند بنابراین تاریخچه مقاطع مخروطی در دوران اسلامی را می توان از سه منظر مورد مطالعه قرارداد که در قسمت های بعد به شرح تک تک آنها خواهیم پرداخت . اول از نظر دانش ریاضیات و هندسه دوم از منظر کاربرد عملی در معماری و سوم کاربرد عملی در دیگر دانش ها ی آن زمان
در مورد کاربرد مقاطع مخروطی در دانش ریاضی در همین بخش توضیح داده و در مورد کاربرد مقاطع مخروطی در سایر علوم و تکنولوژی های مربوط به آن در بخش بعدی توضیح می دهیم .
۸) از منظر علم هندسه و ریاضیات
ریاضیدانان دوره اسلامی دانش مقاطع مخروطی را بسط و گسترش دادند و در بخش های مختلف ریاضی از آن استفاده کردند . ابوجعفر خازن خراسانی ریاضیدان برجسته ایرانی ( او در قرن چهارم هجری زندگی می کرد و بین سال های ۹۶۱و ۹۷۱میلادی درگذشت) توانست به کمک مقاطع مخروطی معادله درجه سوم را حل کند بعد از او بقیه ریاضیدانان هم معادله درجه سوم را به این طریق حل می کردند .
همچنین ابن هیثم (دانشمند نور شناس ایرانی ) هم توانست با استفاده از یک سهمی و هذولی مثلث قائم الزاویه ای طراحی کند که مجموع ضلع کوچک و ارتفاعش با وتر مثلث برابر باشد .( شکل شماره ۳۹ ) این کار در طراحی نوعی کاشیکاری بسیار بکار آمد .
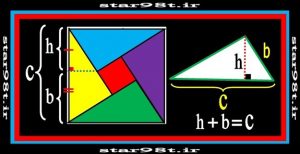
شکل شماره ۳۹ – مثلث قائم الزاویه که وترش برابر مجموع ضلع کوچک و ارتفاعش است با شکل طراحی شده با این مثلث
ابن هیثم همچنین یک مسئلۀ معروف نورشناخت را با استفاده از تقاطع دایره و هذلولی حل کرد. ( شهرت ابن هیثم بیشتر در زمینه نور می باشد . او اولین دانشمند فیزیک نور در جهان است که در زمینه شناخت نور و قانونهای شکست و بازتاب آن نقش مهمی ایفا کردهاست. )
ریاضیدان دیگری به نام ابوسهل بیژن کوهی توانست با استفاده از هذولی یک زاویه را به سه قسمت تقسیم کند.همچنین ابوسهل کوهی پرگاری ابداع کرده بود که با آن پرگار می شد تمام مقاطع مخروطی را رسم کرد .

شکل شماره ۴۰ – ابوجعفر خازن خراسانی

شکل شماره ۴۱ – ابن هیثم

شکل شماره ۴۲ – ابوسهل بیژن کوهی
۱۲- استفاده از مقاطع مخروطی در علوم و تکنولوژی
مقاطع مخروطی استفاده های گسترده ای در علوم و تکنولوژی دارد اهمیت مقاطع مخروطی و همینطور متناظر سه بعدی آنها ( کره و کره گون و… هذولی گون ) در علوم و تکنولوژی بر کسی پوشیده نیست . در اینجا بعضی از کاربردهای مقاطع مخروطی را در علوم و تکنولوژی مورد بررسی قرار می دهیم .
۱) استفاده عملی از مقاطع مخروطی در دوران قدیم
در آن زمان هنوز مدارات سیاره ها شناخته نشده بود و دانش مقاطع مخروطی کاربرد گسترده ای در دانش نجوم نداشت . ولی به کمک مقاطع مخروطی می توانستند ساعت های آفتابی دقیق تری بسازند ولی صنعتگران از مدت ها قبل ساعت های آفتابی را بر اساس جداول و شاخص هائی که تعیین کرده بود می ساختند و نیازی به مقاطع مخروطی نبود.دانشمندانی مانند ابوریحان و خاقانی با استفاده از دانش مقاطع مخروطی اسطرلاب هائی به مراتب دقیق تر ساختند ولی ساخت آنها نیاز به دقت بیشتری داشت و بسیار پرزحمت و پر هزینه تمام می شد . ولی در آن زمان مهمترین استفاده مقاطع مخروطی برای ساخت آینه سوزان بود که سهمی گون کاسه ای بهترین گزینه بود زیرا سهمی گون این خاصیت را دارد که نور را دقیقا در یک جا کانونی کند . راجع به این مطلب درقسمت های بعد توضیح می دهیم .
۲) کتاب “ المخروطات” بنوموسی چگونه به اروپا رسید ؟
دانش مقاطع مخروطی در اروپای بعد از سلطه امپراتوری روم و بعد در قرون وسطی کاملا به فراموشی سپرده شد و بجز دانش های اندک اروپائیان چیزی در این مورد نمی دانستند در حالی که در تمدن اسلامی به همت برادران بنوموسی همانطور که گفته شد استفاده های گسترده ای می کردند . بعد از دوران رنسانس اندک اندک نیاز به این شاخه ریاضی احساس شد و ریاضیدانان آن زمان جسته گریخته مطالبی را کشف کرده بودند . ولی آنقدری نبود که کاملا به کار بیاید ولی بخت با اروپائیان یار بود .
در سال ۱۵۷۸میلادی، اسقف کلیسای انطاکیه تعدادی کتاب های شرقی را به دوک اعظم توسکانی فردیناندو دو مدیچی (دوک مقامی در اروپا همانند حاکم ایالات بود ) به عنوان هدیه داد او هم به کتابدارش (فردیناندو، جیووانی ) سپرد . در میان کتاب ها نسخه ای از” المخروطات” با ویرایش ابوالفتح اصفهانی پیدا کرد او که خود ریاضیدان بود از اهمیت این کتاب آگاه شد و در صدد ترجمه برآمد ولی عمرش کفاف نداد و در گذشت . گالیله که از یافتن کتاب باخبر شده بود در صدد بدست آوردن آن شد ولی نتوانست ( تلاش زیادی نکرد و آنها هم کتاب را به او ندادند ) سرانجام در سال ۱۶۶۱ریاضی دانی به نام “جووانی آلفونسو بورلیِ“ کتاب را ترجمه کرد همزمان دو نسخه اصلی(ازبنوموسی) هم بدست آمدکه درسال۱۶۶۷چاپ شد. و این همزمان با کشف قانون جاذبه عمومی نیوتن و توضیح مدارهای کپلری بر اساس مقاطع مخروطی بود. که مورد استفاده نیوتن هم واقع شد.
۳) مقاطع مخروطی در دنیای امروز
در اروپا با شروع نظریه خورشید مرکزی کپرنیک و بعد کارهای کپلر و ارائه نظریه کپلر مبنی بر این که مدار سیارات به دور خورشید به صورت بیضی می باشد و بعد دستاوردهای قوانین گرانش نیوتن مبنی بر این که مدار هر جسم دور جسم دیگر به یکی از چهار مقطع مخروطی ختم می شود (مدارهای بسته مانند دایره و بیضی و مدارهای باز و برگشت ناپذیر سهمی و هذولی) کاربرد مقاطع مخروطی در نجوم اهمیت بسیاری یافت به صورتی که امروزه برای درک سازو کار حرکت سیارات و گرانش به این مقوله نیاز داریم ( و ما در مقاله “ گرانش “ که بزودی منتشر می شود در مورد آن توضیح می دهیم )
همچنین امروزه در دانش های مختلف همانند : ساختن عدسى ها، وسايل نورى و وسايل پيش بينى هوا، ارتباطات قمرهاى مصنوعى و… همچنین در ساختن پل ها و دانش نور و صدا و امواج رادیوئی کاربرد دارند .
۴) استفاده از مقاطع مخروطی در معماری از قدیم تا کنون
معماران به تدریج فهمیدند که نه تنها در طراحی و زیبا سازی مساجد و بناهای آن زمان نیازمند دانش مقاطع مخروطی هستند بلکه به کمک دانش مقاطع مخروطی ساختمان های مقاوم تر و بهتری می توانند طراحی کنند . ساخت گنبدها و مناره ها با استفاده از مقاطع مخروطی بسیار راحت تر و مفیدتر می باشد . از جمله نوعی گنبد که آب باران را راحت تر هدایت می کند . و بسیار با دوام تر و محکم تر می باشد . همچنین در کاشیکاری و تزئین بناها هم طرح های جالبی را به کمک مقاطع مخروطی می توان رسم کرد .
در اینجا نمونه هائی از موارد استفاده مقاطع مخروطی در معماری و مهندسی عمران می آوریم .
۱- ۴)در کاشیکاری: بسیاری از شکل های روی کاشی ها به کمک مقاطع مخروطی بدست آمده است .
۲-۴) پل کمانی سهموی : اقتصادی ترین و محکم ترین پل ها پل های سهموی هستند .
۳-۴) سازه های هذولی وار : سازههای هُذلولیوار در معماری به گونهای از سازهها میگویند که طرح آنها به شکل هندسی هذلولیوار باشد. نظر به اهمیت آن در قسمت بعدی در مورد آن توضیح می دهیم .
۲) سازه های هذولی شکل
سازه های هذولی وار ( هذولی گون یکپارچه ) به طور گسترده در ساخت برج های بلندی نظیر برج های خنک کننده (نظیر آنچه در برج های خنک کننده نیروگاه ها می بینید ) به کار گرفته می شود که ضمن خفظ زیبائی از استحکام بسیار زیادی هم برخوردار بوده و ضمنا اقتصادی نیز می باشند . همچنین برای سقف بسیاری از استادیوم ها از سازه های هذولی گون زین اسبی هم استفاده می شود . همچنین بسیاری از بناها و ساختمان ها بخاطر زیبائی هم که شده به صورت هذولی گون یکپارچه ساخته می شود(شکل های ۴۳ تا ۴۶)

شکل شماره ۴۳ – نخستین برج هذولی وار جهان در شهر نیژنی نووگورود روسیه

شکل شماره ۴۴ – کلیسای جامع برازیلیا

شکل شماره ۴۵ – برج آب با مخزن چنبره ای در لهستان

شکل شماره ۴۶ – برج خنک کننده هذولی یکپارچه
۳) انعکاس نور از آینه
یکی از خواص آینه ها در این است که نور با هر زاویه ای نسبت به سطح عمود بر آینه به آن برخورد کند با همان زاویه از آینه انعکاس می یابد به صورتی که اگر محل برخورد را راس زاویه گرفته و پرتو برخورد و پرتو انعکاس را دو ضلع زاویه در نظر بگیریم خط عمود بر سطح آینه نیمساز زاویه می شود .
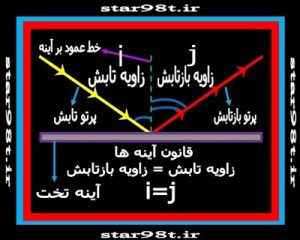
شکل شماره ۴۷ – انعکاس نور از آینه تخت
۴) خاصیت مهم سهمی و آینه های سهموی شکل
از نظر هندسی می توان ثایت کرد که اگر پرتو تابش با پرتو بازتابش برابر باشد (همانند آنچه قانون آینه ها می گوید) و آنگاه یک دسته پرتو موازی و در راستای محور سهمی به یک سهمی برخورد کنند تمام پرتوهای بازتابش در کانون سهمی به هم می رسند . بنابراین سهمی گون کاسه ای بهترین شکلی است که می تواند پرتوها را در یک جا کانونی کند . این مسئله در اپتیک و نور بسیار اهمیت دارد به گونه ای که امروزه تقریبا تمام آینه های تلسکوپ های بزرگ (همان آینه های مقعر که در فیزیک توضیح می دهند) و اکثر رادیو تلسکوپ ها همه قسمتی از یک سهمی گون کاسه ای هستند .
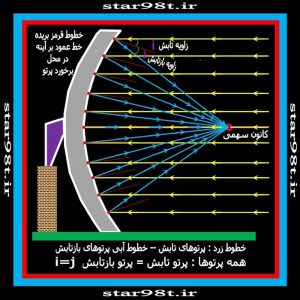
شکل شماره ۴۸ – انعکاس نور از آینه مقعر سهموی کانون آینه و کانون سهمی یکی است
۵) مقایسه آینه کروی و آینه سهموی
گفتیم که برای تلسکوپ های بزرگ از آینه سهموی استفاده می کنند البته این به معنی این نیست که از آینه های کروی ( آینه هائی که قسمتی از یک کره هستند) استفاده نشود . آینه های کروی (بخصوص آینه های بزرگ با قطر ۲۰ سانتیمتر به بالا ) نمی توانند نورهای موازی را که از فاصله دور می آیند درست کانونی کنند مگر این که طول لوله و وزن آن افزایش یابد و این افزایش وزن در تلسکوپ های بزرگ بشدت دردسر آفرین است ولی در تلسکوپ های کوچک ( مانند تلسکوپ های خانگی ) و ارزان قیمت خیلی تفاوت نمی کند .
مزیت آینه های کروی به آینه های سهموی ساخت راحت تر و هزینه به مراتب پائین تر آنها است بنابراین در
آینه های کوره های خورشیدی (و وسائل مشابه ) که دقت کانونی کردن خیلی اهمیت ندارد ترجیحا از آینه های کروی استفاده می شود .
۶) مقاطع مخروطی در نجوم و فیزیک
بعداز این که کپلر قوانین خود را وضع کرد (در مقاله “ گرانش “ در مورد قوانین کپلر توضیحات مفصل می دهیم) و اعلام کرد که مدار سیارات به دور خورشید نه یک دایره که یک بیضی می باشد و نیوتن بعد از وضع قانون جاذبه عمومی به تشریح قوانین کپلر پرداخت و آنها را توضیح داد نتیجه گرفت که هرگاه یک جسم کوچکی جذب جسم بزرگی شود و در روی آن سقوط نکند در مداری قرار می گیرد که لزوما یکی از مقاطع مخروطی می باشد و این به سرعت جسم بستگی دارد اگر سرعت جسم کم باشد مدار حرکت آن دایره و اگر بیشتر باشد بیضی می باشد که هر دو مدارهای بسته (جسم به نقطه اول خود برمی گردد ) هستند ولی سرعت بالاتر باعث می شود مدار جسم به سهمی و هذولی تعغیر کرده و جسم هرگز باز نگردد . همچنین در حرکات پرتابی به سادگی می توان نشان داد که مسیر حرکت جسم یک سهمی می باشد که سرانجام صفحه افق را قطع می کند و سقوط می کند همچنین علم مقاطع مخروطی در بخش های مختلف فیزیک کاربرد گسترده ای دارد .
![]()
برای مطالعه سایر مقاله های نجومی روی شکل زیر کلیک کنید.
![]()
برای مطالعه مقاله های روانشناسی اینجا را کلیک کنید .
![]()
عکس های طبیعت, طبیعت خوانسار , شکوفه های بهاری , گلستان کوه ,دانلود آلبوم های کامل بهترین و زیباترین عکس ها ,آلبوم هائی با صدها عکس کیفیت بالا , در هیچ کجای اینترنت این عکسها را پیدا نمیکنید , عکس هابدون استفاده از تکنیک های فتوشاپ تهیه شده , کاملا طبیعی
![]()
برای آموزش کامل و حرفه ای گوگل مپ روی شکل زیر کلیک کنید
![]()
۱) هر گونه اظهار نظر را در فرم اظهار نظر کاربران وارد کنید .
۲) نظرات بعد از تایید مدیریت نشان داده می شود .
۳) با انتقادات و پیشنهادات سازنده خود ما را هرچه بیشتر همراهی کنید . مدیریت از انتقادات و پیشنهادات سازنده شما استقبال میکند .
۴) نوشته های قرمز پر رنگ ارجاع به لینک هستند که هنوز لینک آنها قرار داده نشده است ( هنوز صفحه آنها منتشر نشده است )
۵) نوشته های آبی پر رنگ ارجاع به لینک هستند که لینک آنها قرار داده شده است ( صفحه آنها منتشر شده است )
۶) هرگونه بهره برداری : کپی تمام و یا قسمتی از مطالب این سایت بدون ارجاع منبع آن ممنوع می باشد .
۷) تکثیر فایل های Pdf با ذکر منبع آزاد ولی فروش آن تحت هر عنوان و با ذکر منبع هم ممنوع می باشد.
![]()